Solve Absolute Value Inequalities
Learning Outcomes
- Express solutions to inequalities containing absolute value
- Identify solutions for absolute inequalities where there are no solutions
Solve Inequalities Containing Absolute Value
Let us apply what you know about solving equations that contain absolute value and what you know about inequalities to solve inequalities that contain absolute value. Let us start with a simple inequality.[latex]\left|x\right|\leq 4[/latex]
This inequality is read, “the absolute value of x is less than or equal to [latex]4[/latex].” If you are asked to solve for x, you want to find out what values of x are [latex]4[/latex] units or less away from [latex]0[/latex] on a number line. You could start by thinking about the number line and what values of x would satisfy this equation. [latex]4[/latex] and [latex]−4[/latex] are both four units away from [latex]0[/latex], so they are solutions. [latex]3[/latex] and [latex]−3[/latex] are also solutions because each of these values is less than [latex]4[/latex] units away from [latex]0[/latex]. So are [latex]1[/latex] and [latex]−1[/latex],[latex]0.5[/latex] and [latex]−0.5[/latex], and so on—there are an infinite number of values for x that will satisfy this inequality. The graph of this inequality will have two closed circles, at [latex]4[/latex] and [latex]−4[/latex]. The distance between these two values on the number line is colored in blue because all of these values satisfy the inequality. The solution can be written this way:
Inequality notation: [latex]-4\leq x\leq4[/latex]
Interval notation: [latex]\left[-4,4\right][/latex]
The situation is a little different when the inequality sign is “greater than” or “greater than or equal to.” Consider the simple inequality [latex]\left|x\right|>3[/latex]. Again, you could think of the number line and what values of x are greater than [latex]3[/latex] units away from zero. This time, [latex]3[/latex] and [latex]−3[/latex] are not included in the solution, so there are open circles on both of these values. [latex]2[/latex] and [latex]−2[/latex] would not be solutions because they are not more than [latex]3[/latex] units away from [latex]0[/latex]. But [latex]5[/latex] and [latex]−5[/latex] would work and so would all of the values extending to the left of [latex]−3[/latex] and to the right of [latex]3[/latex]. The graph would look like the one below.
The solution can be written this way:
Inequality notation: [latex]-4\leq x\leq4[/latex]
Interval notation: [latex]\left[-4,4\right][/latex]
The situation is a little different when the inequality sign is “greater than” or “greater than or equal to.” Consider the simple inequality [latex]\left|x\right|>3[/latex]. Again, you could think of the number line and what values of x are greater than [latex]3[/latex] units away from zero. This time, [latex]3[/latex] and [latex]−3[/latex] are not included in the solution, so there are open circles on both of these values. [latex]2[/latex] and [latex]−2[/latex] would not be solutions because they are not more than [latex]3[/latex] units away from [latex]0[/latex]. But [latex]5[/latex] and [latex]−5[/latex] would work and so would all of the values extending to the left of [latex]−3[/latex] and to the right of [latex]3[/latex]. The graph would look like the one below.
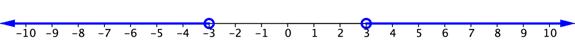 The solution to this inequality can be written this way:
Inequality notation: [latex]x<−3[/latex] or [latex]x>3[/latex].
Interval notation: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex]
In the following video, you will see examples of how to solve and express the solution to absolute value inequalities involving both and and or.
https://youtu.be/0cXxATY2S-k
The solution to this inequality can be written this way:
Inequality notation: [latex]x<−3[/latex] or [latex]x>3[/latex].
Interval notation: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex]
In the following video, you will see examples of how to solve and express the solution to absolute value inequalities involving both and and or.
https://youtu.be/0cXxATY2S-k
Writing Solutions to Absolute Value Inequalities
For any positive value of a and x, a single variable, or any algebraic expression:| Absolute Value Inequality | Equivalent Inequality | Interval Notation |
| [latex]\left|{ x }\right|\le{ a}[/latex] | [latex]{ -a}\le{x}\le{ a}[/latex] | [latex]\left[-a, a\right][/latex] |
| [latex]\left| x \right|\lt{a}[/latex] | [latex]{ -a}\lt{x}\lt{ a}[/latex] | [latex]\left(-a, a\right)[/latex] |
| [latex]\left| x \right|\ge{ a}[/latex] | [latex]{x}\le\text{−a}[/latex] or [latex]{x}\ge{ a}[/latex] | [latex]\left(-\infty,-a\right]\cup\left[a,\infty\right)[/latex] |
| [latex]\left| x \right|\gt\text{a}[/latex] | [latex]\displaystyle{x}\lt\text{−a}[/latex] or [latex]{x}\gt{ a}[/latex] | [latex]\left(-\infty,-a\right)\cup\left(a,\infty\right)[/latex] |
Example
Solve for x. [latex]\left|x+3\right|\gt4[/latex]Answer: Since this is a “greater than” inequality, the solution can be rewritten according to the “greater than” rule.
[latex] \displaystyle x+3<-4\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,\,x+3>4[/latex]
Solve each inequality.[latex]\begin{array}{r}x+3<-4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x+3>4\\\underline{\,\,\,\,-3\,\,\,\,\,-3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,-3\,\,-3}\\x\,\,\,\,\,\,\,\,\,<-7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,>1\\\\x<-7\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,x>1\,\,\,\,\,\,\,\end{array}[/latex]
Check the solutions in the original equation to be sure they work. Check the end point of the first related equation, [latex]−7[/latex] and the end point of the second related equation, 1.[latex] \displaystyle \begin{array}{r}\,\,\,\left| x+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+3 \right|>4\\\left| -7+3 \right|=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 1+3 \right|=4\\\,\,\,\,\,\,\,\left| -4 \right|=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 4 \right|=4\\\,\,\,\,\,\,\,\,\,\,\,\,4=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4=4\end{array}[/latex]
Try [latex]−10[/latex], a value less than [latex]−7[/latex], and 5, a value greater than 1, to check the inequality.[latex] \displaystyle \begin{array}{r}\,\,\,\,\,\left| x+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+3 \right|>4\\\left| -10+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 5+3 \right|>4\\\,\,\,\,\,\,\,\,\,\,\left| -7 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 8 \right|>4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,7>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,8>4\end{array}[/latex]
Both solutions check! Inequality notation: [latex] \displaystyle x<-7\,\,\,\,\,\text{or}\,\,\,\,\,x>1[/latex] Interval notation: [latex]\left(-\infty, -7\right)\cup\left(1,\infty\right)[/latex] Graph: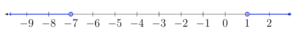
Example
Solve for y. [latex] \displaystyle \mathsf{3}\left| \mathsf{2}\mathrm{y}\mathsf{+6} \right|-\mathsf{9<27}[/latex]Answer: Begin isolating the absolute value by adding 9 to both sides of the inequality.
[latex] \displaystyle \begin{array}{r}3\left| 2y+6 \right|-9<27\\\underline{\,\,+9\,\,\,+9}\\3\left| 2y+6 \right|\,\,\,\,\,\,\,\,<36\end{array}[/latex]
Divide both sides by 3 to isolate the absolute value.[latex]\begin{array}{r}\underline{3\left| 2y+6 \right|}\,<\underline{36}\\3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\,\\\,\,\,\,\,\,\,\,\,\left| 2y+6 \right|<12\end{array}[/latex]
Write the absolute value inequality using the “less than” rule. Subtract 6 from each part of the inequality.[latex]\begin{array}{r}-12<2y+6<12\\\underline{\,\,-6\,\,\,\,\,\,\,\,\,\,\,\,\,-6\,\,\,-6}\\-18\,<\,2y\,\,\,\,\,\,\,\,\,<\,\,6\,\end{array}[/latex]
Divide by [latex]2[/latex] to isolate the variable.[latex]\begin{array}{r}\underline{-18}<\underline{2y}<\underline{\,6\,}\\2\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,2\,\,\\-9<\,\,y\,\,\,\,<\,3\end{array}[/latex]
Answer
Inequality notation: [latex] \displaystyle -9<\,\,y\,\,<3[/latex] Interval notation: [latex]\left(-9,3\right)[/latex] Graph:
Identify Cases of Inequalities Containing Absolute Value That Have No Solutions
As with equations, there may be instances where there is no solution to an inequality.Example
Solve for x. [latex]\left|2x+3\right|+9\leq 7[/latex]Answer: Isolate the absolute value by subtracting [latex]9[/latex] from both sides of the inequality.
[latex] \displaystyle \begin{array}{r}\left| 2x+3 \right|+9\,\le \,\,\,7\,\,\\\underline{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-9\,\,\,\,\,-9}\\\,\,\,\,\,\,\,\left| 2x+3 \right|\,\,\,\le -2\,\end{array}[/latex]
The absolute value of a quantity can never be a negative number, so there is no solution to the inequality. There is no solutionSummary
Inequalities containing absolute value can be solved by rewriting them using compound inequalities. The first step to solving absolute inequalities is to isolate the absolute value. The next step is to decide whether you are working with an or inequality or an and inequality. If the inequality is greater than a number, we will use or. If the inequality is less than a number, we will use and. Remember that if we end up with an absolute value greater than or less than a negative number, there is no solution.Licenses & Attributions
CC licensed content, Shared previously
- Ex 1: Solve and Graph Basic Absolute Value inequalities. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex 2: Solve and Graph Absolute Value inequalities Mathispower4u . Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex 3: Solve and Graph Absolute Value inequalitie. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Ex 4: Solve and Graph Absolute Value inequalities (Requires Isolating Abs. Value). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
