We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Write the Equation of a Linear Function Part II

Learning Outcomes

  • Write the equation of a linear function from a graph
  • Write the equation for a linear function from slope given two points

Now that we have written equations for linear functions using both slope-intercept form and point-slope form, we can choose which method to use based on the information we are given. That information may be provided in the form of a graph, a point and a slope, two points, and so on. Look at the graph of the function f below.

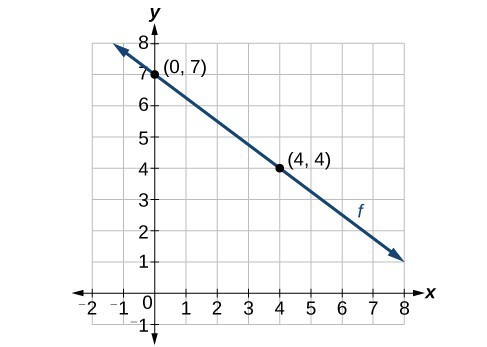
Graph depicting how to calculate the slope of a line

We are not given the slope of the line, but we can choose any two points on the line to find the slope. Choose [latex](0, 7)[/latex] and [latex](4, 4)[/latex]. We can use these points to calculate the slope.

[latex]\begin{array}{l} m & =\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =\dfrac{4 - 7}{4 - 0}\hfill \\ & =-\dfrac{3}{4} \end{array}[/latex]
 

Now we can substitute the slope and the coordinates of one of the points into point-slope form.

[latex]\begin{array}{l}y-{y}_{1}=m\left(x-{x}_{1}\right)\hfill \\ y - 4=-\dfrac{3}{4}\left(x - 4\right)\hfill \end{array}[/latex]
 

If we want to rewrite the equation in slope-intercept form, we would do the following:

[latex]\begin{array}{l}y - 4=-\dfrac{3}{4}\left(x - 4\right)\hfill \\ y - 4=-\dfrac{3}{4}x+3\hfill \\ \text{ }y=-\dfrac{3}{4}x+7\hfill \end{array}[/latex]

If we wanted to find the equation of the line in slope-intercept form without first using point-slope form, we could have recognized that the line crosses the y-axis when the output value is [latex]7[/latex]. Therefore, b = [latex]7[/latex]. We now have the initial value b and the slope m so we can substitute m and b into slope-intercept form of a line.

The function is [latex]f\left(x\right)=-\dfrac{3}{4}x+7[/latex], and the linear equation would be [latex]y=-\dfrac{3}{4}x+7[/latex].

How To: Given the graph of a linear function, write an equation to represent the function

  1. Identify two points on the line.
  2. Use the two points to calculate the slope.
  3. Determine where the line crosses the y-axis to identify the y-intercept by visual inspection.
  4. Substitute the slope and y-intercept into slope-intercept form of a linear equation.

Example

Write an equation for a linear function f given its graph shown below.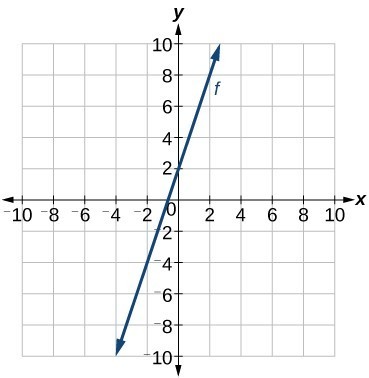 Graph of an increasing function with points at (-3, 0) and (0, 1).

Answer:

Identify two points on the line such as [latex](0, 2)[/latex] and [latex](–2, –4)[/latex]. Use the points to calculate the slope.

[latex]\begin{array}{l}m & =\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =\dfrac{-4 - 2}{-2 - 0}\hfill \\ & =\dfrac{-6}{-2}\hfill \\ & =3\hfill \end{array}[/latex]
 

Substitute the slope and the coordinates of one of the points into point-slope form.

[latex]\begin{array}{l}y-{y}_{1}=m\left(x-{x}_{1}\right)\\ y-\left(-4\right)=3\left(x-\left(-2\right)\right)\\ y+4=3\left(x+2\right)\end{array}[/latex]
 

We can use algebra to rewrite the equation in slope-intercept form.

[latex-display]\begin{array}{l}y+4=3\left(x+2\right)\hfill \\ y+4=3x+6\hfill \\ y=3x+2 \hfill \end{array}[/latex-display]   This makes sense because we can see from the graph above that the line crosses the y-axis at the point [latex](0,2)[/latex], which is the y-intercept, so [latex]b=2[/latex]

In the following video, we show an example of how to write the equation of a line given its graph. https://youtu.be/mmWf_oLTNSQ

Example

If f is a linear function, with [latex]f\left(3\right)=-2[/latex] , and [latex]f\left(8\right)=1[/latex], find an equation for the function in slope-intercept form.

Answer:

We can write the given points using coordinates.

[latex]\begin{array}{l}f\left(3\right)=-2\to \left(3,-2\right)\hfill \\ f\left(8\right)=1\to \left(8,1\right)\hfill \end{array}[/latex]
 

We can then use the points to calculate the slope.

[latex]\begin{array}{l} m & =\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =\dfrac{1-\left(-2\right)}{8 - 3}\hfill \\ & =\dfrac{3}{5}\hfill \end{array}[/latex]
 

Substitute the slope and the coordinates of one of the points into point-slope form.

[latex]\begin{array}\text{ }y-{y}_{1}=m\left(x-{x}_{1}\right)\hfill \\ y-\left(-2\right)=\dfrac{3}{5}\left(x - 3\right)\hfill \end{array}[/latex]
 

We can use algebra to rewrite the equation in slope-intercept form.

[latex]\begin{array}{l}y+2=\dfrac{3}{5}\left(x - 3\right)\hfill \\ y+2=\dfrac{3}{5}x-\dfrac{9}{5}\hfill \\ \text{ }y=\dfrac{3}{5}x-\dfrac{19}{5}\hfill \end{array}[/latex]

In the video we show another example of how to write a linear function given two points written with function notation. https://youtu.be/TSIcryAtCmY

Summary

  • Given a graph, you can write the equation of the line it represents.
  • This method only works for graphs that have points that are easy to verify by visual inspection.

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Ex 1: Find the Equation of a Line in Slope Intercept Form Given the Graph of a Line. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • College Algebra. Provided by: OpenStax Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download free at : http://cnx.org/contents/[email protected]:1/Preface.
  • Ex: Find the Linear Function Given Two Function Values in Function Notation. Authored by: for Lumen Learning. License: CC BY: Attribution.