Solve Systems by Substitution
Learning Outcomes
- Solve systems of equations by substitution
- Identify inconsistent systems of equations containing two variables
How To: Given a system of two equations in two variables, solve using the substitution method
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, and then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the other variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
Example
Solve the following system of equations by substitution.Answer: First, we will solve the first equation for [latex]y[/latex].
[latex]\begin{array}{llll}-x+y=-5\hfill & \hfill & \hfill & \hfill \\ -\left(8\right)+\left(3\right)=-5\hfill & \hfill & \hfill & \text{True}\hfill \\ 2x - 5y=1\hfill & \hfill & \hfill & \hfill \\ 2\left(8\right)-5\left(3\right)=1\hfill & \hfill & \hfill & \text{True}\hfill \end{array}[/latex]
The substitution method can be used to solve any linear system in two variables, but the method works best if one of the equations contains a coefficient of 1 or [latex]–1[/latex] so that we do not have to deal with fractions.Example
Solve the following system of equations.[latex]\begin{array}{l}x=9 - 2y\hfill \\ x+2y=13\hfill \end{array}[/latex]
Answer: We can approach this problem in two ways. Because one equation is already solved for x, the most obvious step is to use substitution. We can substitute the expression [latex]9-2y[/latex] for [latex]x[/latex] in the second equation.
[latex]\begin{array}{r}x+2y=13\hfill \\ \left(9 - 2y\right)+2y=13\hfill \\ 9+0y=13\hfill \\ 9=13\hfill \end{array}[/latex]
Clearly, this statement is a contradiction because [latex]9\ne 13[/latex]. Therefore, the system has no solution. The second approach would be to first manipulate the equations so that they are both in slope-intercept form. We manipulate the first equation as follows.[latex]\begin{array}{l}\text{ }x=9 - 2y\hfill \\ 2y=-x+9\hfill \\ \text{ }y=-\dfrac{1}{2}x+\dfrac{9}{2}\hfill \end{array}[/latex]
We then convert the second equation to slope-intercept form.[latex]\begin{array}{l}x+2y=13\hfill \\ \text{ }2y=-x+13\hfill \\ \text{ }y=-\dfrac{1}{2}x+\dfrac{13}{2}\hfill \end{array}[/latex]
Comparing the equations, we see that they have the same slope but different y-intercepts. Therefore, the lines are parallel and do not intersect.[latex]\begin{array}{l}\begin{array}{l}\\ y=-\dfrac{1}{2}x+\dfrac{9}{2}\end{array}\hfill \\ y=-\dfrac{1}{2}x+\dfrac{13}{2}\hfill \end{array}[/latex]
Writing the equations in slope-intercept form confirms that the system is inconsistent because all lines will intersect eventually unless they are parallel. Parallel lines will never intersect; thus, the two lines have no points in common. The graphs of the equations in this example are shown below.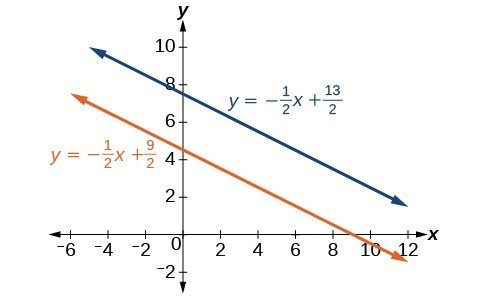
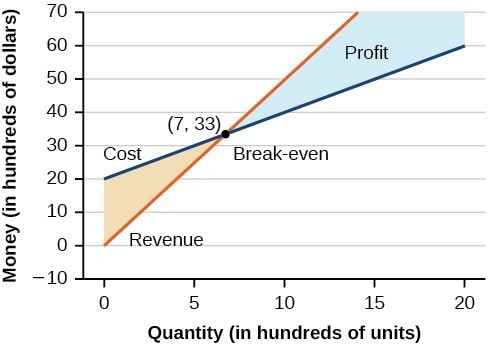 The point at which the two lines intersect is called the break-even point. We can see from the graph that if 700 units are produced, the cost is [latex]$3,300[/latex] and the revenue is also [latex]$3,300[/latex]. In other words, the company breaks even if they produce and sell 700 units. They neither make money nor lose money.
The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss.
The point at which the two lines intersect is called the break-even point. We can see from the graph that if 700 units are produced, the cost is [latex]$3,300[/latex] and the revenue is also [latex]$3,300[/latex]. In other words, the company breaks even if they produce and sell 700 units. They neither make money nor lose money.
The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The shaded region to the left represents quantities for which the company suffers a loss.
Example
Given the cost function [latex]C\left(x\right)=0.85x+35,000[/latex] and the revenue function [latex]R\left(x\right)=1.55x[/latex], find the break-even point.Answer: Write the system of equations using [latex]y[/latex] to replace function notation.
[latex]\begin{array}{l}\begin{array}{l}\\ y=0.85x+35,000\end{array}\hfill \\ y=1.55x\hfill \end{array}[/latex]
Substitute the expression [latex]0.85x+35,000[/latex] from the first equation into the second equation and solve for [latex]x[/latex].[latex]\begin{array}{c}0.85x+35,000=1.55x\\ 35,000=0.7x\\ 50,000=x\end{array}[/latex]
Then, substitute [latex]x=50,000[/latex] into either the cost function or the revenue function.[latex]1.55\left(50,000\right)=77,500[/latex]
The break-even point is [latex]\left(50,000,77,500\right)[/latex]. The cost to produce [latex]50,000[/latex] units is [latex]$77,500[/latex], and the revenue from the sales of [latex]50,000[/latex] units is also [latex]$77,500[/latex]. To make a profit, the business must produce and sell more than [latex]50,000[/latex] units.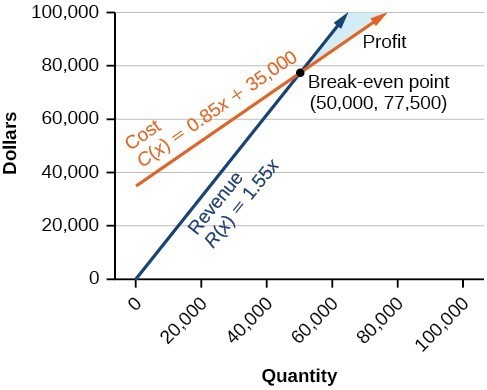 The company will make a profit after [latex]50,000[/latex] units are produced.
The company will make a profit after [latex]50,000[/latex] units are produced.
Example
The cost of a ticket to the circus is [latex]$25.00[/latex] for children and [latex]$50.00[/latex] for adults. On a certain day, attendance at the circus is [latex]2,000[/latex] and the total gate revenue is [latex]$70,000[/latex]. How many children and how many adults bought tickets?Answer: Let [latex]c=[/latex] the number of children and [latex]a=[/latex] the number of adults in attendance. The total number of people is [latex]2,000[/latex]. We can use this to write an equation for the number of people at the circus that day.
[latex]c+a=2,000[/latex]
The revenue from all children can be found by multiplying [latex]$25.00[/latex] by the number of children, [latex]25c[/latex]. The revenue from all adults can be found by multiplying [latex]$50.00[/latex] by the number of adults, [latex]50a[/latex]. The total revenue is [latex]$70,000[/latex]. We can use this to write an equation for the revenue.[latex]25c+50a=70,000[/latex]
We now have a system of linear equations in two variables.[latex]\begin{array}{c}c+a=2,000\\ 25c+50a=70,000\end{array}[/latex]
In the first equation, the coefficient of both variables is [latex]1[/latex]. We can quickly solve the first equation for either [latex]c[/latex] or [latex]a[/latex]. We will solve for [latex]a[/latex].[latex]\begin{array}{c}c+a=2,000\\ a=2,000-c\end{array}[/latex]
Substitute the expression [latex]2,000-c[/latex] in the second equation for [latex]a[/latex] and solve for [latex]c[/latex].[latex]\begin{array}{l} 25c+50\left(2,000-c\right)=70,000\hfill \\ 25c+100,000 - 50c=70,000\hfill \\ -25c=-30,000\hfill \\ c=1,200\hfill \end{array}[/latex]
Substitute [latex]c=1,200[/latex] into the first equation to solve for [latex]a[/latex].[latex]\begin{array}{l}1,200+a=2,000\hfill \\ a=800\hfill \end{array}[/latex]
We find that [latex]1,200[/latex] children and [latex]800[/latex] adults bought tickets to the circus that day.Licenses & Attributions
CC licensed content, Shared previously
- Ex 2: Solve a System of Equations Using Substitution. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
- Ex: Solve a System of Equations Using Substitution - No Solution. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Solve a System of Equations Using Substitution - Infinite Solutions. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Solve an Application Problem Using a System of Linear Equations (09x-43). Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
