We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Prealgebra

Applications with Pi

Learning Outcomes

  • Find the circumference of a circle
  • Find the area of a circle
  The properties of circles have been studied for over [latex]2,000[/latex] years. All circles have exactly the same shape, but their sizes are affected by the length of the radius, a line segment from the center to any point on the circle. A line segment that passes through a circle’s center connecting two points on the circle is called a diameter. The diameter is twice as long as the radius. See the image below. The size of a circle can be measured in two ways. The distance around a circle is called its circumference. A circle is shown. A dotted line running through the widest portion of the circle is labeled as a diameter. A dotted line from the center of the circle to a point on the circle is labeled as a radius. Along the edge of the circle is the circumference. Archimedes discovered that for circles of all different sizes, dividing the circumference by the diameter always gives the same number. The value of this number is pi, symbolized by Greek letter [latex]\pi [/latex] (pronounced "pie"). However, the exact value of [latex]\pi [/latex] cannot be calculated since the decimal never ends or repeats (we will learn more about numbers like this in The Properties of Real Numbers.) Doing the Manipulative Mathematics activity Pi Lab will help you develop a better understanding of pi. If we want the exact circumference or area of a circle, we leave the symbol [latex]\pi [/latex] in the answer. We can get an approximate answer by substituting [latex]3.14[/latex] as the value of [latex]\pi [/latex]. We use the symbol [latex]\approx [/latex] to show that the result is approximate, not exact.

Properties of Circles

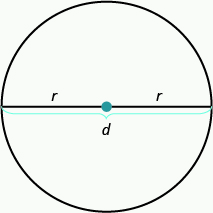
A circle is shown. A line runs through the widest portion of the circle. There is a red dot at the center of the circle. The half of the line from the center of the circle to a point on the right of the circle is labeled with an r. The half of the line from the center of the circle to a point on the left of the circle is also labeled with an r. The two sections labeled r have a brace drawn underneath showing that the entire segment is labeled d. [latex-display]\begin{array}{c}r\text{ is the length of the radius.}\hfill \\ d\text{ is the length of the diameter.}\hfill \end{array}[/latex-display] [latex-display]\begin{array}{cccc}\text{The circumference is }2\pi \mathit{\text{r}}.\hfill & & & C=2\pi \mathit{\text{r}}\hfill \\ \text{The area is }\pi{\mathit{\text{r}}}^{2}.\hfill & & & A=\pi{\mathit{\text{r}}}^{2}\hfill \end{array}[/latex-display]
  Since the diameter is twice the radius, another way to find the circumference is to use the formula [latex]C=\pi \mathit{\text{d}}[/latex]. Suppose we want to find the exact area of a circle of radius [latex]10[/latex] inches. To calculate the area, we would evaluate the formula for the area when [latex]r=10[/latex] inches and leave the answer in terms of [latex]\pi[/latex]. [latex-display]\begin{array}{}\\ A=\pi {\mathit{\text{r}}}^{2}\hfill \\ A=\pi \text{(}{10}^{2}\text{)}\hfill \\ A=\pi \cdot 100\hfill \end{array}[/latex-display] We write [latex]\pi [/latex] after the [latex]100[/latex]. So the exact value of the area is [latex]A=100\pi [/latex] square inches. To approximate the area, we would substitute [latex]\pi \approx 3.14[/latex]. [latex-display]\begin{array}{ccc}A& =& 100\pi \hfill \\ \\ & \approx & 100\cdot 3.14\hfill \\ & \approx & 314\text{ square inches}\hfill \end{array}[/latex-display] Remember to use square units, such as square inches, when you calculate the area.  

example

A circle has radius [latex]10[/latex] centimeters. Approximate its ⓐ circumference and ⓑ area. Solution
ⓐ Find the circumference when [latex]r=10[/latex].
Write the formula for circumference. [latex]C=2\pi \mathit{\text{r}}[/latex]
Substitute [latex]3.14[/latex] for [latex]\pi [/latex] and 10 for , [latex]r[/latex] . [latex]C\approx 2\left(3.14\right)\left(10\right)[/latex]
Multiply. [latex]C\approx 62.8\text{ centimeters}[/latex]
ⓑ Find the area when [latex]r=10[/latex].
Write the formula for area. [latex]A=\pi {\mathit{\text{r}}}^{2}[/latex]
Substitute [latex]3.14[/latex] for [latex]\pi [/latex] and 10 for [latex]r[/latex] . [latex]A\approx \left(3.14\right){\text{(}10\text{)}}^{2}[/latex]
Multiply. [latex]A\approx 314\text{ square centimeters}[/latex]
 

try it

[ohm_question]146563[/ohm_question]
   

example

A circle has radius [latex]42.5[/latex] centimeters. Approximate its ⓐ circumference and ⓑ area.

Answer: Solution

ⓐ Find the circumference when [latex]r[/latex]=[latex]42.5[/latex].
Write the formula for circumference. [latex]C=2\pi \mathit{\text{r}}[/latex]
Substitute [latex]3.14[/latex] for [latex]\pi [/latex] and [latex]42.5[/latex] for [latex]r[/latex] [latex]C\approx 2\left(3.14\right)\left(42.5\right)[/latex]
Multiply. [latex]C\approx 266.9\text{ centimeters}[/latex]
ⓑ Find the area when [latex]r=42.5[/latex] .
Write the formula for area. [latex]A=\pi {\mathit{\text{r}}}^{2}[/latex]
Substitute [latex]3.14[/latex] for [latex]\pi [/latex] and [latex]42.5[/latex] for [latex]r[/latex] . [latex]A\approx \left(3.14\right){\text{(}42.5\text{)}}^{2}[/latex]
Multiply. [latex]A\approx 5671.625\text{ square centimeters}[/latex]

 

try it

[ohm_question]146564[/ohm_question]
Watch the following video to see another example of how to find the circumference of a circle. https://youtu.be/sHtsnC2Mgnk In the next video example, we find the area of a circle. https://youtu.be/SIKkWLqt2mQ

Approximate [latex]\pi [/latex] with a Fraction

Convert the fraction [latex]\frac{22}{7}[/latex] to a decimal. If you use your calculator, the decimal number will fill up the display and show [latex]3.14285714[/latex]. But if we round that number to two decimal places, we get [latex]3.14[/latex], the decimal approximation of [latex]\pi [/latex]. When we have a circle with radius given as a fraction, we can substitute [latex]\frac{22}{7}[/latex] for [latex]\pi [/latex] instead of [latex]3.14[/latex]. And, since [latex]\frac{22}{7}[/latex] is also an approximation of [latex]\pi [/latex], we will use the [latex]\approx [/latex] symbol to show we have an approximate value.  

example

A circle has radius [latex]\frac{14}{15}[/latex] meter. Approximate its ⓐ circumference and ⓑ area.

Answer: Solution

ⓐ Find the circumference when [latex]r=\frac{14}{15}[/latex].
Write the formula for circumference. [latex]C=2\pi \mathit{\text{r}}[/latex]
Substitute [latex]\frac{22}{7}[/latex] for [latex]\pi [/latex] and [latex]\frac{14}{15}[/latex] for [latex]r[/latex] . [latex]C\approx 2\left(\frac{22}{7}\right)\left(\frac{14}{15}\right)[/latex]
Multiply. [latex]C\approx \frac{88}{15}\text{meters}[/latex]
ⓑ Find the area when [latex]r=\frac{14}{15}[/latex].
Write the formula for area. [latex]A=\pi {\mathit{\text{r}}}^{2}[/latex]
Substitute [latex]\frac{22}{7}[/latex] for [latex]\pi [/latex] and [latex]\frac{14}{15}[/latex] for [latex]r[/latex] . [latex]A\approx \left(\frac{22}{7}\right){\text{(}\frac{14}{15}\text{)}}^{2}[/latex]
Multiply. [latex]A\approx \frac{616}{225}\text{square meters}[/latex]

 

try it

[ohm_question]146611[/ohm_question]
 

Licenses & Attributions

CC licensed content, Original

  • Question ID 146611, 146564, 146563. Authored by: Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously

  • Examples: Determine the Circumference of a Circle. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
  • Example: Determine the Area of a Circle. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.

CC licensed content, Specific attribution