A cube is a rectangular solid whose length, width, and height are equal. See Volume and Surface Area of a Cube, below. Substituting, s for the length, width and height into the formulas for volume and surface area of a rectangular solid, we get:
[latex-display]\begin{array}{ccccc}V=LWH\hfill & & & & S=2LH+2LW+2WH\hfill \\ V=s\cdot s\cdot s\hfill & & & & S=2s\cdot s+2s\cdot s+2s\cdot s\hfill \\ V={s}^{3}\hfill & & & & S=2{s}^{2}+2{s}^{2}+2{s}^{2}\hfill \\ & & & & S=6{s}^{2}\hfill \end{array}[/latex-display]
So for a cube, the formulas for volume and surface area are [latex]V={s}^{3}[/latex] and [latex]S=6{s}^{2}[/latex].
Volume and Surface Area of a Cube
For any cube with sides of length [latex]s[/latex],

example
A cube is [latex]2.5[/latex] inches on each side. Find its 1. volume and 2. surface area.
Solution
Step 1 is the same for both 1. and 2., so we will show it just once.
| Step 1. Read the problem. Draw the figure and
label it with the given information. |
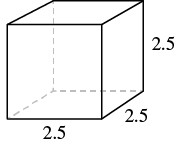 |
| 1. |
|
| Step 2. Identify what you are looking for. |
the volume of the cube |
| Step 3. Name. Choose a variable to represent it. |
let V = volume |
| Step 4. Translate.
Write the appropriate formula. |
[latex]V={s}^{3}[/latex] |
| Step 5. Solve. Substitute and solve. |
[latex]V={\left(2.5\right)}^{3}[/latex]
[latex]V=15.625[/latex] |
| Step 6. Check: Check your work. |
|
| Step 7. Answer the question. |
The volume is [latex]15.625[/latex] cubic inches. |
| 2. |
|
| Step 2. Identify what you are looking for. |
the surface area of the cube |
| Step 3. Name. Choose a variable to represent it. |
let S = surface area |
| Step 4. Translate.
Write the appropriate formula. |
[latex]S=6{s}^{2}[/latex] |
| Step 5. Solve. Substitute and solve. |
[latex]S=6\cdot {\left(2.5\right)}^{2}[/latex]
[latex]S=37.5[/latex] |
| Step 6. Check: The check is left to you. |
|
| Step 7. Answer the question. |
The surface area is [latex]37.5[/latex] square inches. |
example
A notepad cube measures [latex]2[/latex] inches on each side. Find its 1. volume and 2. surface area.
Answer:
Solution
| Step 1. Read the problem. Draw the figure and
label it with the given information. |
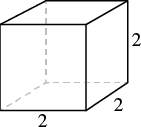 |
| 1. |
|
| Step 2. Identify what you are looking for. |
the volume of the cube |
| Step 3. Name. Choose a variable to represent it. |
let V = volume |
| Step 4. Translate.
Write the appropriate formula. |
[latex]V={s}^{3}[/latex] |
| Step 5. Solve the equation. |
[latex]V={2}^{3}[/latex]
[latex]V=8[/latex] |
| Step 6. Check: Check that you did the calculations
correctly. |
|
| Step 7. Answer the question. |
The volume is [latex]8[/latex] cubic inches. |
| 2. |
|
| Step 2. Identify what you are looking for. |
the surface area of the cube |
| Step 3. Name. Choose a variable to represent it. |
let S = surface area |
| Step 4. Translate.
Write the appropriate formula. |
[latex]S=6{s}^{2}[/latex] |
| Step 5. Solve the equation. |
[latex]S=6\cdot {2}^{2}[/latex]
[latex]S=24[/latex] |
| Step 6. Check: The check is left to you. |
|
| Step 7. Answer the question. |
The surface area is [latex]24[/latex] square inches. |



