Graphing a Line Given a Point and a Slope
Learning Outcomes
- Graph a line given the slope and a point on the line
In this chapter, we graphed lines by plotting points, by using intercepts, and by recognizing horizontal and vertical lines.
Another method we can use to graph lines is the point-slope method. Sometimes, we will be given one point and the slope of the line, instead of its equation. When this happens, we use the definition of slope to draw the graph of the line.
example
Graph the line passing through the point [latex]\left(1,-1\right)[/latex] whose slope is [latex]m=\frac{3}{4}[/latex]. Solution Plot the given point, [latex]\left(1,-1\right)[/latex].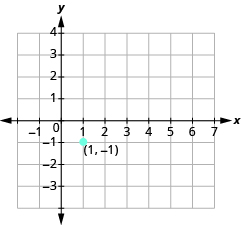 Use the slope formula [latex]m=\frac{\text{rise}}{\text{run}}[/latex] to identify the rise and the run.
[latex-display]\begin{array}{}\\ \\ m=\frac{3}{4}\hfill \\ \frac{\text{rise}}{\text{run}}=\frac{3}{4}\hfill \\ \\ \\ \text{rise}=3\hfill \\ \text{run}=4\hfill \end{array}[/latex-display]
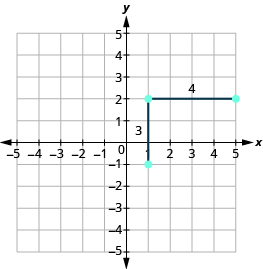
Starting at the point we plotted, count out the rise and run to mark the second point. We count [latex]3[/latex] units up and [latex]4[/latex] units right.
Use the slope formula [latex]m=\frac{\text{rise}}{\text{run}}[/latex] to identify the rise and the run.
[latex-display]\begin{array}{}\\ \\ m=\frac{3}{4}\hfill \\ \frac{\text{rise}}{\text{run}}=\frac{3}{4}\hfill \\ \\ \\ \text{rise}=3\hfill \\ \text{run}=4\hfill \end{array}[/latex-display]
Starting at the point we plotted, count out the rise and run to mark the second point. We count [latex]3[/latex] units up and [latex]4[/latex] units right.
 Then we connect the points with a line and draw arrows at the ends to show it continues.
Then we connect the points with a line and draw arrows at the ends to show it continues.
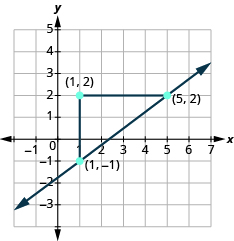 We can check our line by starting at any point and counting up [latex]3[/latex] and to the right [latex]4[/latex]. We should get to another point on the line.
We can check our line by starting at any point and counting up [latex]3[/latex] and to the right [latex]4[/latex]. We should get to another point on the line.
try it
[ohm_question]147024[/ohm_question]Graph a line given a point and a slope
- Plot the given point.
- Use the slope formula to identify the rise and the run.
- Starting at the given point, count out the rise and run to mark the second point.
- Connect the points with a line.
example
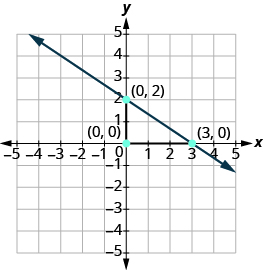
Graph the line with [latex]y[/latex] -intercept [latex]\left(0,2\right)[/latex] and slope [latex]m=-\frac{2}{3}[/latex].Answer:
Solution
Plot the given point, the [latex]y[/latex] -intercept [latex]\left(0,2\right)[/latex].
 Use the slope formula [latex]m=\frac{\text{rise}}{\text{run}}[/latex] to identify the rise and the run.
[latex-display]\begin{array}{}\\ \\ m=-\frac{2}{3}\hfill \\ \frac{\text{rise}}{\text{run}}=\frac{-2}{3}\hfill \\ \\ \\ \text{rise}=-2\hfill \\ \text{run}=3\hfill \end{array}[/latex-display]
Starting at [latex]\left(0,2\right)[/latex], count the rise and the run and mark the second point.
Use the slope formula [latex]m=\frac{\text{rise}}{\text{run}}[/latex] to identify the rise and the run.
[latex-display]\begin{array}{}\\ \\ m=-\frac{2}{3}\hfill \\ \frac{\text{rise}}{\text{run}}=\frac{-2}{3}\hfill \\ \\ \\ \text{rise}=-2\hfill \\ \text{run}=3\hfill \end{array}[/latex-display]
Starting at [latex]\left(0,2\right)[/latex], count the rise and the run and mark the second point.
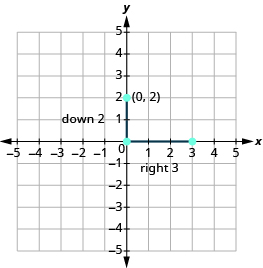 Connect the points with a line.
Connect the points with a line.
try it
[ohm_question]147025[/ohm_question]example
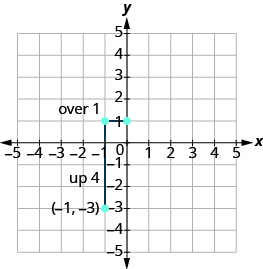
Graph the line passing through the point [latex]\left(-1,-3\right)[/latex] whose slope is [latex]m=4[/latex].Answer:
Solution
Plot the given point.

| Identify the rise and the run. | [latex]m=4[/latex] |
| Write [latex]4[/latex] as a fraction. | [latex]\frac{\text{rise}}{\text{run}}=\frac{4}{1}[/latex] |
| [latex]\text{rise}=4\text{run}=1[/latex] |
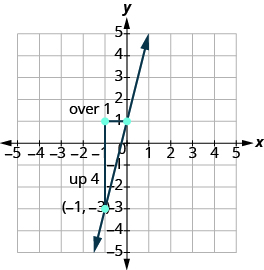
 Mark the second point. Connect the two points with a line.
Mark the second point. Connect the two points with a line.
try it
[ohm_question]147026[/ohm_question]Solve Slope Applications
At the beginning of this section, we said there are many applications of slope in the real world. Let’s look at a few now.example
The pitch of a building’s roof is the slope of the roof. Knowing the pitch is important in climates where there is heavy snowfall. If the roof is too flat, the weight of the snow may cause it to collapse. What is the slope of the roof shown?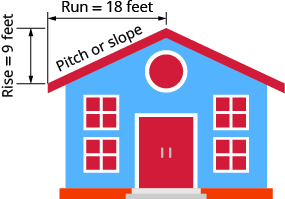
Answer: Solution
| Use the slope formula. | [latex]m=\frac{\text{rise}}{\text{run}}[/latex] |
| Substitute the values for rise and run. | [latex]m=\frac{\text{9 ft}}{\text{18 ft}}[/latex] |
| Simplify. | [latex]m=\frac{1}{2}[/latex] |
| The slope of the roof is [latex]\frac{1}{2}[/latex] . |
try it
[ohm_question]147027[/ohm_question]example
Have you ever thought about the sewage pipes going from your house to the street? Their slope is an important factor in how they take waste away from your house. Sewage pipes must slope down [latex]\frac{1}{4}[/latex] inch per foot in order to drain properly. What is the required slope?
Answer: Solution
| Use the slope formula. | [latex]m=\frac{\text{rise}}{\text{run}}[/latex] |
| [latex]m=\frac{-\frac{1}{4}\text{in}\text{.}}{1\text{ft}}[/latex] | |
| [latex]m=\frac{-\frac{1}{4}\text{in}\text{.}}{1\text{ft}}[/latex] | |
| Convert [latex]1[/latex] foot to [latex]12[/latex] inches. | [latex]m=\frac{-\frac{1}{4}\text{in}\text{.}}{12\text{in.}}[/latex] |
| Simplify. | [latex]m=-\frac{1}{48}[/latex] |
| The slope of the pipe is [latex]-\frac{1}{48}[/latex]. |
try it
[ohm_question]147028[/ohm_question]Licenses & Attributions
CC licensed content, Original
- Question ID 147028, 147027, 147026. Authored by: Lumen Learning. License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
