Locating and Ordering Fractions and Mixed Numbers on the Number Line
Learning Outcomes
- Locate and label improper and proper fractions on a number line
- Order fractions and mixed numbers on a number line
- Use inequality symbols to compare fractions and mixed numbers
 The proper fractions listed are [latex]\frac{1}{5}[/latex] and [latex]\frac{4}{5}[/latex]. We know proper fractions have values less than one, so [latex]\frac{1}{5}[/latex] and [latex]\frac{4}{5}[/latex] are located between the whole numbers [latex]0[/latex] and [latex]1[/latex]. The denominators are both [latex]5[/latex], so we need to divide the segment of the number line between [latex]0[/latex] and [latex]1[/latex] into five equal parts. We can do this by drawing four equally spaced marks on the number line, which we can then label as [latex]\frac{1}{5},\frac{2}{5},\frac{3}{5}[/latex], and [latex]\frac{4}{5}[/latex].
Now plot points at [latex]\frac{1}{5}[/latex] and [latex]\frac{4}{5}[/latex].
The proper fractions listed are [latex]\frac{1}{5}[/latex] and [latex]\frac{4}{5}[/latex]. We know proper fractions have values less than one, so [latex]\frac{1}{5}[/latex] and [latex]\frac{4}{5}[/latex] are located between the whole numbers [latex]0[/latex] and [latex]1[/latex]. The denominators are both [latex]5[/latex], so we need to divide the segment of the number line between [latex]0[/latex] and [latex]1[/latex] into five equal parts. We can do this by drawing four equally spaced marks on the number line, which we can then label as [latex]\frac{1}{5},\frac{2}{5},\frac{3}{5}[/latex], and [latex]\frac{4}{5}[/latex].
Now plot points at [latex]\frac{1}{5}[/latex] and [latex]\frac{4}{5}[/latex].
 The only mixed number to plot is [latex]3\frac{1}{3}[/latex]. Between what two whole numbers is [latex]3\frac{1}{3}?[/latex] Remember that a mixed number is a whole number plus a proper fraction, so [latex]3\frac{1}{3}>3[/latex]. Since it is greater than [latex]3[/latex], but not a whole unit greater, [latex]3\frac{1}{3}[/latex] is between [latex]3[/latex] and [latex]4[/latex]. We need to divide the portion of the number line between [latex]3[/latex] and [latex]4[/latex] into three equal pieces (thirds) and plot [latex]3\frac{1}{3}[/latex] at the first mark.
The only mixed number to plot is [latex]3\frac{1}{3}[/latex]. Between what two whole numbers is [latex]3\frac{1}{3}?[/latex] Remember that a mixed number is a whole number plus a proper fraction, so [latex]3\frac{1}{3}>3[/latex]. Since it is greater than [latex]3[/latex], but not a whole unit greater, [latex]3\frac{1}{3}[/latex] is between [latex]3[/latex] and [latex]4[/latex]. We need to divide the portion of the number line between [latex]3[/latex] and [latex]4[/latex] into three equal pieces (thirds) and plot [latex]3\frac{1}{3}[/latex] at the first mark.
 Finally, look at the improper fractions [latex]\frac{7}{4},\frac{9}{2}[/latex], and [latex]\frac{8}{3}[/latex]. Locating these points will be easier if you change each of them to a mixed number.
[latex-display]\frac{7}{4}=1\frac{3}{4},\frac{9}{2}=4\frac{1}{2},\frac{8}{3}=2\frac{2}{3}[/latex-display]
Here is the number line with all the points plotted.
Finally, look at the improper fractions [latex]\frac{7}{4},\frac{9}{2}[/latex], and [latex]\frac{8}{3}[/latex]. Locating these points will be easier if you change each of them to a mixed number.
[latex-display]\frac{7}{4}=1\frac{3}{4},\frac{9}{2}=4\frac{1}{2},\frac{8}{3}=2\frac{2}{3}[/latex-display]
Here is the number line with all the points plotted.

Example
Locate and label the following on a number line: [latex]\frac{3}{4},\frac{4}{3},\frac{5}{3},4\frac{1}{5}[/latex], and [latex]\frac{7}{2}[/latex]. Solution: Start by locating the proper fraction [latex]\frac{3}{4}[/latex]. It is between [latex]0[/latex] and [latex]1[/latex]. To do this, divide the distance between [latex]0[/latex] and [latex]1[/latex] into four equal parts. Then plot [latex]\frac{3}{4}[/latex].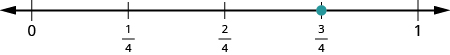 Next, locate the mixed number [latex]4\frac{1}{5}[/latex]. It is between [latex]4[/latex] and [latex]5[/latex] on the number line. Divide the number line between [latex]4[/latex] and [latex]5[/latex] into five equal parts, and then plot [latex]4\frac{1}{5}[/latex] one-fifth of the way between [latex]4[/latex] and [latex]5[/latex] .
Next, locate the mixed number [latex]4\frac{1}{5}[/latex]. It is between [latex]4[/latex] and [latex]5[/latex] on the number line. Divide the number line between [latex]4[/latex] and [latex]5[/latex] into five equal parts, and then plot [latex]4\frac{1}{5}[/latex] one-fifth of the way between [latex]4[/latex] and [latex]5[/latex] .
 Now locate the improper fractions [latex]\frac{4}{3}[/latex] and [latex]\frac{5}{3}[/latex] .
It is easier to plot them if we convert them to mixed numbers first.
[latex-display]\frac{4}{3}=1\frac{1}{3},\frac{5}{3}=1\frac{2}{3}[/latex-display]
Divide the distance between [latex]1[/latex] and [latex]2[/latex] into thirds.
Now locate the improper fractions [latex]\frac{4}{3}[/latex] and [latex]\frac{5}{3}[/latex] .
It is easier to plot them if we convert them to mixed numbers first.
[latex-display]\frac{4}{3}=1\frac{1}{3},\frac{5}{3}=1\frac{2}{3}[/latex-display]
Divide the distance between [latex]1[/latex] and [latex]2[/latex] into thirds.
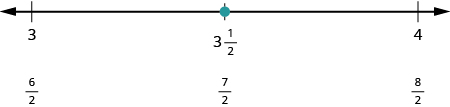
 Next let us plot [latex]\frac{7}{2}[/latex]. We write it as a mixed number, [latex]\frac{7}{2}=3\frac{1}{2}[/latex] . Plot it between [latex]3[/latex] and [latex]4[/latex].
Next let us plot [latex]\frac{7}{2}[/latex]. We write it as a mixed number, [latex]\frac{7}{2}=3\frac{1}{2}[/latex] . Plot it between [latex]3[/latex] and [latex]4[/latex].
 The number line shows all the numbers located on the number line.
The number line shows all the numbers located on the number line.

try it
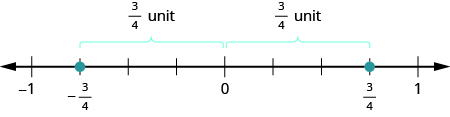
#146007 [ohm_question height="270"]146007[/ohm_question] #146008 [ohm_question height="270"]146008[/ohm_question] Fractions have opposites, too. The opposite of [latex]\frac{3}{4}[/latex] is [latex]-\frac{3}{4}[/latex]. It is the same distance from [latex]0[/latex] on the number line, but on the opposite side of [latex]0[/latex].
Fractions have opposites, too. The opposite of [latex]\frac{3}{4}[/latex] is [latex]-\frac{3}{4}[/latex]. It is the same distance from [latex]0[/latex] on the number line, but on the opposite side of [latex]0[/latex].
 Thinking of negative fractions as the opposite of positive fractions will help us locate them on the number line. To locate [latex]-\frac{15}{8}[/latex] on the number line, first think of where [latex]\frac{15}{8}[/latex] is located. It is an improper fraction, so we first convert it to the mixed number [latex]1\frac{7}{8}[/latex] and see that it will be between [latex]1[/latex] and [latex]2[/latex] on the number line. So its opposite, [latex]-\frac{15}{8}[/latex], will be between [latex]-1[/latex] and [latex]-2[/latex] on the number line.
Thinking of negative fractions as the opposite of positive fractions will help us locate them on the number line. To locate [latex]-\frac{15}{8}[/latex] on the number line, first think of where [latex]\frac{15}{8}[/latex] is located. It is an improper fraction, so we first convert it to the mixed number [latex]1\frac{7}{8}[/latex] and see that it will be between [latex]1[/latex] and [latex]2[/latex] on the number line. So its opposite, [latex]-\frac{15}{8}[/latex], will be between [latex]-1[/latex] and [latex]-2[/latex] on the number line.

Example
Locate and label the following on the number line: [latex]\frac{1}{4},-\frac{1}{4},1\frac{1}{3},-1\frac{1}{3},\frac{5}{2}[/latex], and [latex]-\frac{5}{2}[/latex].Answer:
Solution:
Draw a number line. Mark [latex]0[/latex] in the middle and then mark several units to the left and right.
To locate [latex]\frac{1}{4}[/latex], divide the interval between [latex]0[/latex] and [latex]1[/latex] into four equal parts. Each part represents one-quarter of the distance. So plot [latex]\frac{1}{4}[/latex] at the first mark.
 To locate [latex]-\frac{1}{4}[/latex], divide the interval between [latex]0[/latex] and [latex]-1[/latex] into four equal parts. Plot [latex]-\frac{1}{4}[/latex] at the first mark to the left of [latex]0[/latex].
To locate [latex]-\frac{1}{4}[/latex], divide the interval between [latex]0[/latex] and [latex]-1[/latex] into four equal parts. Plot [latex]-\frac{1}{4}[/latex] at the first mark to the left of [latex]0[/latex].
 Since [latex]1\frac{1}{3}[/latex] is between [latex]1[/latex] and [latex]2[/latex], divide the interval between [latex]1[/latex] and [latex]2[/latex] into three equal parts. Plot [latex]1\frac{1}{3}[/latex] at the first mark to the right of [latex]1[/latex]. Then since [latex]-1\frac{1}{3}[/latex] is the opposite of [latex]1\frac{1}{3}[/latex] it is between [latex]-1[/latex] and [latex]-2[/latex]. Divide the interval between [latex]-1[/latex] and [latex]-2[/latex] into three equal parts. Plot [latex]-1\frac{1}{3}[/latex] at the first mark to the left of [latex]-1[/latex].
Since [latex]1\frac{1}{3}[/latex] is between [latex]1[/latex] and [latex]2[/latex], divide the interval between [latex]1[/latex] and [latex]2[/latex] into three equal parts. Plot [latex]1\frac{1}{3}[/latex] at the first mark to the right of [latex]1[/latex]. Then since [latex]-1\frac{1}{3}[/latex] is the opposite of [latex]1\frac{1}{3}[/latex] it is between [latex]-1[/latex] and [latex]-2[/latex]. Divide the interval between [latex]-1[/latex] and [latex]-2[/latex] into three equal parts. Plot [latex]-1\frac{1}{3}[/latex] at the first mark to the left of [latex]-1[/latex].
 To locate [latex]\frac{5}{2}[/latex] and [latex]-\frac{5}{2}[/latex], it may be helpful to rewrite them as the mixed numbers [latex]2\frac{1}{2}[/latex] and [latex]-2\frac{1}{2}[/latex].
Since [latex]2\frac{1}{2}[/latex] is between [latex]2[/latex] and [latex]3[/latex], divide the interval between [latex]2[/latex] and [latex]3[/latex] into two equal parts. Plot [latex]\frac{5}{2}[/latex] at the mark. Then since [latex]-2\frac{1}{2}[/latex] is between [latex]-2[/latex] and [latex]-3[/latex], divide the interval between [latex]-2[/latex] and [latex]-3[/latex] into two equal parts. Plot [latex]-\frac{5}{2}[/latex] at the mark.
To locate [latex]\frac{5}{2}[/latex] and [latex]-\frac{5}{2}[/latex], it may be helpful to rewrite them as the mixed numbers [latex]2\frac{1}{2}[/latex] and [latex]-2\frac{1}{2}[/latex].
Since [latex]2\frac{1}{2}[/latex] is between [latex]2[/latex] and [latex]3[/latex], divide the interval between [latex]2[/latex] and [latex]3[/latex] into two equal parts. Plot [latex]\frac{5}{2}[/latex] at the mark. Then since [latex]-2\frac{1}{2}[/latex] is between [latex]-2[/latex] and [latex]-3[/latex], divide the interval between [latex]-2[/latex] and [latex]-3[/latex] into two equal parts. Plot [latex]-\frac{5}{2}[/latex] at the mark.

Try it
#146009 [ohm_question height="270"]146009[/ohm_question] #146011 [ohm_question height="270"]146011[/ohm_question]Order Fractions and Mixed Numbers
We can use the inequality symbols to order fractions. Remember that [latex]a>b[/latex] means that [latex]a[/latex] is to the right of [latex]b[/latex] on the number line. As we move from left to right on a number line, the values increase.Example
Order each of the following pairs of numbers, using [latex]<[/latex]; or [latex]>:[/latex]- [latex]-\frac{2}{3}[/latex] __ [latex]- 1[/latex]
- [latex]-3\frac{1}{2}[/latex] __ [latex]- 3[/latex]
- [latex]-\frac{3}{7}-[/latex] __ [latex]\frac{3}{8}[/latex]
- [latex]-2[/latex] __ [latex]\frac{-16}{9}[/latex]
Answer:
Solution:
1. [latex]-\frac{2}{3}>-1[/latex]
 2. [latex]-3\frac{1}{2}<-3[/latex]
2. [latex]-3\frac{1}{2}<-3[/latex]
 3. [latex]-\frac{3}{7}\text{<}-\frac{3}{8}[/latex]
3. [latex]-\frac{3}{7}\text{<}-\frac{3}{8}[/latex]
 4. [latex]-2<\frac{-16}{9}[/latex]
4. [latex]-2<\frac{-16}{9}[/latex]

Try it
#146013 [ohm_question height="270"]146013[/ohm_question] #146012 [ohm_question height="270"]146012[/ohm_question]Licenses & Attributions
CC licensed content, Original
- Question ID: 146007, 146008, 146009, 146011, 146012, 146013. Authored by: Alyson Day. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
CC licensed content, Shared previously
- Ex: Identify a Fraction on a Number Line. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- Determine Negative Proper and Improper Fractions on the Number Line. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Prealgebra. Provided by: OpenStax License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
