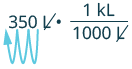We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Prealgebra

Making Unit Conversions in the Metric System of Measurement

Learning Outcomes

  • Convert between Metric units of length, volume, and mass

Make Unit Conversions in the Metric System

In the metric system, units are related by powers of [latex]10[/latex]. The root words of their names reflect this relation. For example, the basic unit for measuring length is a meter. One kilometer is [latex]1000[/latex] meters; the prefix kilo- means thousand. One centimeter is [latex]\frac{1}{100}[/latex] of a meter, because the prefix centi- means one one-hundredth (just like one cent is [latex]\frac{1}{100}[/latex] of one dollar). The equivalencies of measurements in the metric system are shown in the reference table below. The common abbreviations for each measurement are given in parentheses.
Metric Measurements
Length Mass Volume/Capacity
[latex]1[/latex] kilometer (km) = [latex]1000[/latex] m [latex]1[/latex] hectometer (hm) = [latex]100[/latex] m [latex]1[/latex] dekameter (dam) = [latex]10[/latex] m [latex]1[/latex] meter (m) = [latex]1[/latex] m [latex]1[/latex] decimeter (dm) = [latex]0.1[/latex] m [latex]1[/latex] centimeter (cm) = [latex]0.01[/latex] m [latex]1[/latex] millimeter (mm) = [latex]0.001[/latex] m [latex]1[/latex] kilogram (kg) = [latex]1000[/latex] g [latex]1[/latex] hectogram (hg) = [latex]100[/latex] g [latex]1[/latex] dekagram (dag) = [latex]10[/latex] g [latex]1[/latex] gram (g) = [latex]1[/latex] g [latex]1[/latex] decigram (dg) = [latex]0.1[/latex] g [latex]1[/latex] centigram (cg) = [latex]0.01[/latex] g [latex]1[/latex] milligram (mg) = [latex]0.001[/latex] g [latex]1[/latex] kiloliter (kL) = [latex]1000[/latex] L [latex]1[/latex] hectoliter (hL) = [latex]100[/latex] L [latex]1[/latex] dekaliter (daL) = [latex]10[/latex] L [latex]1[/latex] liter (L) = [latex]1[/latex] L [latex]1[/latex] deciliter (dL) = [latex]0.1[/latex] L [latex]1[/latex] centiliter (cL) = [latex]0.01[/latex] L [latex]1[/latex] milliliter (mL) = [latex]0.001[/latex] L
[latex]1[/latex] meter = [latex]100[/latex] centimeters [latex]1[/latex] meter = [latex]1000[/latex] millimeters [latex]1[/latex] gram = [latex]100[/latex] centigrams [latex]1[/latex] gram = [latex]1000[/latex] milligrams [latex]1[/latex] liter = [latex]100[/latex] centiliters [latex]1[/latex] liter = [latex]1000[/latex] milliliters
To make conversions in the metric system, we will use the same technique we did in the U.S. system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units. Have you ever run a [latex]\text{5 k}[/latex] or [latex]\text{10 k}[/latex] race? The lengths of those races are measured in kilometers. The metric system is commonly used in the United States when talking about the length of a race.

example

Nick ran a [latex]\text{10-kilometer}[/latex] race. How many meters did he run? (credit: William Warby, Flickr) A photograph of 8 male runners in a track race. Solution We will convert kilometers to meters using the Identity Property of Multiplication and the equivalencies in the reference table from earlier.
[latex]10[/latex] kilometers
Multiply the measurement to be converted by [latex]1[/latex]. [latex]10 \color{red}{km}\cdot 1[/latex]
Write [latex]1[/latex] as a fraction relating kilometers and meters. [latex]10 \color{red}{km}\cdot \frac{1000 m}{1\color{red}{km}}[/latex]
Simplify. [latex]\frac{10\color{red}{km}\cdot 1000 m}{1\color{red}{km}}[/latex]
Multiply. [latex]10,000[/latex] m
Nick ran [latex]10,000[/latex] meters.
 

try it

[ohm_question]146841[/ohm_question] [ohm_question]146842[/ohm_question]
 

example

Eleanor’s newborn baby weighed [latex]3200[/latex] grams. How many kilograms did the baby weigh?

Answer: Solution We will convert grams to kilograms.

[latex]3200 \color{red}{grams}[/latex]
Multiply the measurement to be converted by [latex]1[/latex]. [latex]3200 \color{red}{g}\cdot 1[/latex]
Write [latex]1[/latex] as a fraction relating kilograms and grams. [latex]3200 \color{red}{g}\cdot \frac{1 kg}{1000 \color{red}{g}}[/latex]
Simplify. [latex]3200 \color{red}{g}\cdot \frac{1 kg}{1000 \color{red}{g}}[/latex]
Multiply. [latex]\frac{3200 kilograms}{1000}[/latex]
Divide. [latex]3.2[/latex] kilograms
The baby weighed [latex]3.2[/latex] kilograms.

   

try it

[ohm_question]146844[/ohm_question] [ohm_question]146845[/ohm_question]
  Since the metric system is based on multiples of ten, conversions involve multiplying by multiples of ten. In Decimal Operations, we learned how to simplify these calculations by just moving the decimal. To multiply by [latex]10,100,\text{or}1000[/latex], we move the decimal to the right [latex]1,2,\text{or}3[/latex] places, respectively. To multiply by [latex]0.1,0.01,\text{or}0.001[/latex] we move the decimal to the left [latex]1,2,\text{or}3[/latex] places respectively. We can apply this pattern when we make measurement conversions in the metric system. In the previous example, we changed [latex]3200[/latex] grams to kilograms by multiplying by [latex]\frac{1}{1000}\left(\text{or}0.001\right)[/latex]. This is the same as moving the decimal [latex]3[/latex] places to the left. Multiplying 3200 by 1 over 1000 gives 3.2. Notice that the answer, 3.2, is similar to the original value, 3200, just with the decimal moved three places to the left.

example

Convert: 1. [latex]350[/latex] liters to kiloliters 2. [latex]4.1[/latex] liters to milliliters.

Answer: Solution 1. We will convert liters to kiloliters. In the reference table, we see that [latex]\text{1 kiloliter}=\text{1000 liters}[/latex].

[latex]350[/latex] L
Multiply by [latex]1[/latex], writing [latex]1[/latex] as a fraction relating liters to kiloliters. [latex]350 L \cdot \frac{1 kl}{1000 L}[/latex]
Simplify. [latex]350 \color{blue}{L} \cdot \frac{1 kl}{1000 \color{blue}{L}}[/latex]
Move the decimal [latex]3[/latex] units to the left. .
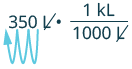[latex]0.35[/latex] kL
2. We will convert liters to milliliters. In the reference table, we see that [latex]\text{1 liter}=1000\text{milliliters.}[/latex]
[latex]4.1[/latex] L
Multiply by [latex]1[/latex], writing [latex]1[/latex] as a fraction relating milliliters to liters. [latex]4.1 L \cdot \frac{1000 ml}{1 L}[/latex]
Simplify. [latex]4.1 L \color{blue}{L} \cdot \frac{1000 ml}{1 \color{blue}{L}}[/latex]
Move the decimal [latex]3[/latex] units to the right. .
[latex]4100[/latex] mL

 

try it

  [ohm_question]146868[/ohm_question] [ohm_question]146869[/ohm_question]   [ohm_question]146870[/ohm_question] [ohm_question]146871[/ohm_question]
 

Use Mixed Units of Measurement in the Metric System

Performing arithmetic operations on measurements with mixed units of measures in the metric system requires the same care we used in the U.S. system. But it may be easier because of the relation of the units to the powers of [latex]10[/latex]. We still must make sure to add or subtract like units.

example

Ryland is [latex]1.6[/latex] meters tall. His younger brother is [latex]85[/latex] centimeters tall. How much taller is Ryland than his younger brother?

Answer: Solution We will subtract the lengths in meters. Convert [latex]85[/latex] centimeters to meters by moving the decimal [latex]2[/latex] places to the left; [latex]85[/latex] cm is the same as [latex]0.85[/latex] m. Now that both measurements are in meters, subtract to find out how much taller Ryland is than his brother. [latex-display]\begin{array}{}\\ \\ \hfill \text{1.60 m}\\ \hfill \underset{\text{_______}}{\text{-0.85 m}}\\ \hfill \text{0.75 m}\end{array}[/latex-display] Ryland is [latex]0.75[/latex] meters taller than his brother.

 

try it

[ohm_question]146872[/ohm_question]
 

example

Dena’s recipe for lentil soup calls for [latex]150[/latex] milliliters of olive oil. Dena wants to triple the recipe. How many liters of olive oil will she need?

Answer: Solution We will find the amount of olive oil in milliliters then convert to liters.

Triple [latex]150[/latex] mL
Translate to algebra. [latex]3\cdot 150\text{mL}[/latex]
Multiply. [latex]450\text{mL}[/latex]
Convert to liters. [latex]450\text{mL}\cdot \frac{0.001\text{L}}{1\text{mL}}[/latex]
Simplify. [latex]0.45\text{L}[/latex]
Dena needs [latex]0.45[/latex] liter of olive oil.

 

try it

[ohm_question]146873[/ohm_question] [ohm_question]146874[/ohm_question]
 

Licenses & Attributions

CC licensed content, Original

  • Question ID 146874, 146873, 146872, 146871, 146870, 146869, 146868. Authored by: Lumen Learning. License: CC BY: Attribution.

CC licensed content, Specific attribution