We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

מדריכי לימוד > Prealgebra

Modeling Squares and Finding the Square Root of a Number

Learning Outcomes

  • Find the square root of of perfect square
  • Explain why the square root of a negative number is not a real number
 

Simplify Expressions with Square Roots

To start this section, we need to review some important vocabulary and notation. Remember that when a number [latex]n[/latex] is multiplied by itself, we can write this as [latex]{n}^{2}[/latex], which we read aloud as "n squared". For example, [latex]{8}^{2}[/latex] is read as "8 squared". We call [latex]64[/latex] the square of [latex]8[/latex] because [latex]{8}^{2}=64[/latex]. Similarly, [latex]121[/latex] is the square of [latex]11[/latex], because [latex]{11}^{2}=121[/latex].

Square of a Number

If [latex]{n}^{2}=m[/latex], then [latex]m[/latex] is the square of [latex]n[/latex].
  Modeling Squares Do you know why we use the word square? If we construct a square with three tiles on each side, the total number of tiles would be nine. A square is shown with 3 tiles on each side. There are a total of 9 tiles in the square. This is why we say that the square of three is nine. [latex-display]{3}^{2}=9[/latex-display] The number [latex]9[/latex] is called a perfect square because it is the square of a whole number. Doing the Manipulative Mathematics activity Square Numbers will help you develop a better understanding of perfect square numbers The chart shows the squares of the counting numbers [latex]1[/latex] through [latex]15[/latex]. You can refer to it to help you identify the perfect squares. A table with two columns is shown. The first column is labeled

Perfect Squares

A perfect square is the square of a whole number.
  What happens when you square a negative number? [latex-display]\begin{array}{cc}\hfill {\left(-8\right)}^{2}& =\left(-8\right)\left(-8\right)\\ & =64\hfill \end{array}[/latex-display] When we multiply two negative numbers, the product is always positive. So, the square of a negative number is always positive. The chart shows the squares of the negative integers from [latex]-1[/latex] to [latex]-15[/latex]. A table is shown with 2 columns. The first column is labeled Did you notice that these squares are the same as the squares of the positive numbers?

Square Roots

Sometimes we will need to look at the relationship between numbers and their squares in reverse. Because [latex]{10}^{2}=100[/latex], we say [latex]100[/latex] is the square of [latex]10[/latex]. We can also say that [latex]10[/latex] is a square root of [latex]100[/latex].

Square Root of a Number

A number whose square is [latex]m[/latex] is called a square root of [latex]m[/latex]. If [latex]{n}^{2}=m[/latex], then [latex]n[/latex] is a square root of [latex]m[/latex].
  Notice [latex]{\left(-10\right)}^{2}=100[/latex] also, so [latex]-10[/latex] is also a square root of [latex]100[/latex]. Therefore, both [latex]10[/latex] and [latex]-10[/latex] are square roots of [latex]100[/latex]. So, every positive number has two square roots: one positive and one negative. What if we only want the positive square root of a positive number? The radical sign, [latex]\sqrt{\phantom{0}}[/latex], stands for the positive square root. The positive square root is also called the principal square root.

Square Root Notation

[latex-display]\sqrt{m}[/latex] is read as "the square root of [latex]m\text{."}[/latex-display] [latex]\text{If}m={n}^{2},\text{then}\sqrt{m}=n\text{for}\text{n}\ge 0[/latex].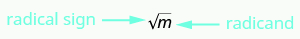 A picture of an m inside a square root sign is shown. The sign is labeled as a radical sign and the m is labeled as the radicand.
  We can also use the radical sign for the square root of zero. Because [latex]{0}^{2}=0,\sqrt{0}=0[/latex]. Notice that zero has only one square root. The chart shows the square roots of the first [latex]15[/latex] perfect square numbers. A table is shown with 2 columns. The first column contains the values: square root of 1, square root of 4, square root of 9, square root of 16, square root of 25, square root of 36, square root of 49, square root of 64, square root of 81, square root of 100, square root of 121, square root of 144, square root of 169, square root of 196, and square root of 225. The second column contains the values: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, and 15.

example

Simplify: ⓐ [latex]\sqrt{25}[/latex] ⓑ [latex]\sqrt{121}[/latex].

Answer: Solution [latex-display]\begin{array}{cccc}\text{(a)}\hfill & & & \\ & & & \sqrt{25}\hfill \\ \text{Since}{5}^{2}=25\hfill & & & 5\hfill \\ \\ \text{(b)}\hfill & & & \\ & & & \sqrt{121}\hfill \\ \text{Since}{11}^{2}=121\hfill & & & 11\hfill \end{array}[/latex-display]

 

try it

[ohm_question]146618[/ohm_question]
The following video shows several more examples of how to simplify the square root of a perfect square. https://youtu.be/rDpIm_EepcE Every positive number has two square roots and the radical sign indicates the positive one. We write [latex]\sqrt{100}=10[/latex]. If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, [latex]-\sqrt{100}=-10[/latex].  

example

Simplify. ⓐ [latex]-\sqrt{9}[/latex] ⓑ [latex]-\sqrt{144.}[/latex]

Answer: Solution

ⓐ
[latex]-\sqrt{9}[/latex]
The negative is in front of the radical sign. [latex]-3[/latex]
ⓑ
[latex]-\sqrt{144}[/latex]
The negative is in front of the radical sign. [latex]-12[/latex]

 

try it

[ohm_question]146619[/ohm_question]
 

Square Root of a Negative Number

Can we simplify [latex]\sqrt{-25}?[/latex] Is there a number whose square is [latex]-25?[/latex] [latex-display]{\left(\right)}^{2}=-25?[/latex-display] None of the numbers that we have dealt with so far have a square that is [latex]-25[/latex]. Why? Any positive number squared is positive, and any negative number squared is also positive. In the next chapter we will see that all the numbers we work with are called the real numbers. So we say there is no real number equal to [latex]\sqrt{-25}[/latex]. If we are asked to find the square root of any negative number, we say that the solution is not a real number.  

example

Simplify: ⓐ [latex]\sqrt{-169}[/latex] ⓑ [latex]-\sqrt{121}[/latex].

Answer: Solution ⓐ There is no real number whose square is [latex]-169[/latex]. Therefore, [latex]\sqrt{-169}[/latex] is not a real number. ⓑ The negative is in front of the radical sign, so we find the opposite of the square root of [latex]121[/latex].

[latex]-\sqrt{121}[/latex]
The negative is in front of the radical. [latex]-11[/latex]

 

try it

[ohm_question]146620[/ohm_question]
 

Licenses & Attributions

CC licensed content, Original

  • Question ID 146620, 146619, 146618. Authored by: Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously

  • Simplify Square Roots (Perfect Squares). Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.

CC licensed content, Specific attribution