We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Prealgebra

Multiplying Decimals

Learning Outcomes

  • Multiply two decimals together
  • Multiply a decimal by 10, 100, or 1000
 

Multiplying decimals is very much like multiplying whole numbers—we just have to determine where to place the decimal point. The procedure for multiplying decimals will make sense if we first review multiplying fractions. Do you remember how to multiply fractions? To multiply fractions, you multiply the numerators and then multiply the denominators. So let’s see what we would get as the product of decimals by converting them to fractions first. We will do two examples side-by-side below. Look for a pattern.

A B
[latex]\left(0.3\right)\left(0.7\right)[/latex] [latex]\left(0.2\right)\left(0.46\right)[/latex]
Convert to fractions. [latex]\left(\frac{3}{10}\right)\left(\frac{7}{10}\right)[/latex] [latex]\left(\frac{2}{10}\right)\left(\frac{46}{100}\right)[/latex]
Multiply. [latex]\frac{21}{100}[/latex] [latex]\frac{92}{1000}[/latex]
Convert back to decimals. [latex]0.21[/latex] [latex]0.092[/latex]
There is a pattern that we can use. In A, we multiplied two numbers that each had one decimal place, and the product had two decimal places. In B, we multiplied a number with one decimal place by a number with two decimal places, and the product had three decimal places. How many decimal places would you expect for the product of [latex]\left(0.01\right)\left(0.004\right)?[/latex] If you said "five", you recognized the pattern. When we multiply two numbers with decimals, we count all the decimal places in the factors—in this case two plus three—to get the number of decimal places in the product—in this case five. 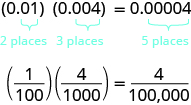The top line says 0.01 times 0.004 equals 0.00004. Below the 0.01, it says 2 places. Below the 0.004, it says 3 places. Below the 0.00004, it says 5 places. The bottom line says 1 over 100 times 4 over 1000 equals 4 over 100,000. Once we know how to determine the number of digits after the decimal point, we can multiply decimal numbers without converting them to fractions first. The number of decimal places in the product is the sum of the number of decimal places in the factors. The rules for multiplying positive and negative numbers apply to decimals, too, of course.

Multiplying Two Numbers

When multiplying two numbers,
  • if their signs are the same, the product is positive.
  • if their signs are different, the product is negative.
When you multiply signed decimals, first determine the sign of the product and then multiply as if the numbers were both positive. Finally, write the product with the appropriate sign.

Multiply decimal numbers.

  1. Determine the sign of the product.
  2. Write the numbers in vertical format, lining up the numbers on the right.
  3. Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
  4. Place the decimal point. The number of decimal places in the product is the sum of the number of decimal places in the factors. If needed, use zeros as placeholders.
  5. Write the product with the appropriate sign.
 

example

Multiply: [latex]\left(3.9\right)\left(4.075\right)[/latex]. Solution
[latex]\left(3.9\right)\left(4.075\right)[/latex]
Determine the sign of the product. The signs are the same. The product will be positive.
Write the numbers in vertical format, lining up the numbers on the right. .
Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points. .
Place the decimal point. Add the number of decimal places in the factors [latex]\left(1+3\right)[/latex]. Place the decimal point 4 places from the right. .
The product is positive. [latex]\left(3.9\right)\left(4.075\right)=15.8925[/latex]
 

try it

[ohm_question]146594[/ohm_question] [ohm_question]146596[/ohm_question]
   

example

Multiply: [latex]\left(-8.2\right)\text{(}5.19\text{).}[/latex]

Answer: Solution

[latex]\left(-8.2\right)\left(5.19\right)[/latex]
The signs are different. The product will be negative.
Write in vertical format, lining up the numbers on the right. [latex]\begin{array}{c}\hfill 5.19\\ \hfill \underset{\text{_____}}{\times 8.2}\end{array}[/latex]
Multiply. [latex]\begin{array}{c}\hfill 5.19\\ \hfill \underset{\text{_____}}{\times 8.2}\\ \hfill 1038\\ \underset{\text{_____}}{4152}\\ \hfill 42558\end{array}[/latex]
. [latex]\begin{array}{c}\hfill 5.19\\ \hfill \underset{\text{_____}}{\times 8.2}\\ \hfill 1038\\ \underset{\text{_____}}{4152}\\ \hfill 42.558\end{array}[/latex]
The product is negative. [latex]\left(-8.2\right)\left(5.19\right)=-42.558[/latex]

 

try it

[ohm_question]146597[/ohm_question]
In the following video we show another example of how to multiply two decimals. https://youtu.be/55OtS_Dil1Y In the next example, we’ll need to add several placeholder zeros to properly place the decimal point.  

example

Multiply: [latex]\left(0.03\right)\text{(}0.045\text{).}[/latex]

Answer: Solution

[latex]\left(0.03\right)\left(0.045\right)[/latex]
The product is positive.
Write in vertical format, lining up the numbers on the right. .
Multiply. .
. Add zeros as needed to get the [latex]5[/latex] places. .
The product is positive. [latex]\left(0.03\right)\left(0.045\right)=0.00135[/latex]

 

try it

[ohm_question]146598[/ohm_question]
 

Multiply by Powers of [latex]10[/latex]

In many fields, especially in the sciences, it is common to multiply decimals by powers of [latex]10[/latex]. Let’s see what happens when we multiply [latex]1.9436[/latex] by some powers of [latex]10[/latex].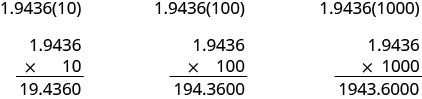 The top row says 1.9436 times 10, then 1.9436 times 100, then 1.9436 times 1000. Below each is a vertical multiplication problem. These show that 1.9436 times 10 is 19.4360, 1.9436 times 100 is 194.3600, and 1.9436 times 1000 is 1943.6000. Look at the results without the final zeros. Do you notice a pattern? [latex-display]\begin{array}{ccc}1.9436\left(10\right)\hfill & =& 19.436\hfill \\ 1.9436\left(100\right)\hfill & =& 194.36\hfill \\ 1.9436\left(1000\right)\hfill & =& 1943.6\hfill \end{array}[/latex-display] The number of places that the decimal point moved is the same as the number of zeros in the power of ten. The table below summarizes the results.
Multiply by Number of zeros Number of places decimal point moves
[latex]10[/latex] [latex]1[/latex] [latex]1[/latex] place to the right
[latex]100[/latex] [latex]2[/latex] [latex]2[/latex] places to the right
[latex]1,000[/latex] [latex]3[/latex] [latex]3[/latex] places to the right
[latex]10,000[/latex] [latex]4[/latex] [latex]4[/latex] places to the right
We can use this pattern as a shortcut to multiply by powers of ten instead of multiplying using the vertical format. We can count the zeros in the power of [latex]10[/latex] and then move the decimal point that same of places to the right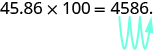. So, for example, to multiply [latex]45.86[/latex] by [latex]100[/latex], move the decimal point [latex]2[/latex] places to the right. 45.86 times 100 is shown to equal 4586. There is an arrow from the decimal going over 2 places from after the 5 to after the 6. Sometimes when we need to move the decimal point, there are not enough decimal places. In that case, we use zeros as placeholders. For example, let’s multiply [latex]2.4[/latex] by [latex]100[/latex]. We need to move the decimal point [latex]2[/latex] places to the right. Since there is only one digit to the right of the decimal point, we must write a [latex]0[/latex] in the hundredths place. 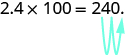2.4 times 100 is shown to equal 240. There is an arrow from the decimal going over 2 places from after the 2 to after the 0.

Multiply a decimal by a power of [latex]10[/latex]

  1. Move the decimal point to the right the same number of places as the number of zeros in the power of [latex]10[/latex].
  2. Write zeros at the end of the number as placeholders if needed.
 

example

Multiply [latex]5.63[/latex] by factors of ⓐ [latex]10[/latex] ⓑ [latex]100[/latex] ⓒ [latex]1000[/latex].

Answer: Solution By looking at the number of zeros in the multiple of ten, we see the number of places we need to move the decimal to the right.

ⓐ
[latex]56.3\left(10\right)[/latex]
There is [latex]1[/latex] zero in [latex]10[/latex], so move the decimal point [latex]1[/latex] place to the right. .
[latex]56.3[/latex]
ⓑ
[latex]5.63\left(100\right)[/latex]
There are [latex]2[/latex] zeros in [latex]100[/latex], so move the decimal point [latex]2[/latex] places to the right. .
[latex]563[/latex]
ⓒ
[latex]5.63\left(1000\right)[/latex]
There are [latex]3[/latex] zeros in [latex]1000[/latex], so move the decimal point [latex]3[/latex] places to the right. .
A zero must be added at the end. [latex]5,630[/latex]

 

Key Takeaways

[ohm_question]146599[/ohm_question]
In the following video we show more examples of how to multiply a decimal by 10, 100, and 1000. https://youtu.be/JFAwf01nPG8

Licenses & Attributions

CC licensed content, Original

  • Multiply Decimals by 10, 100, and 1000. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Question ID 146599 , 146598, 146597, 146596,146594. Authored by: Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously

CC licensed content, Specific attribution