We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Prealgebra

Problem Set 8: Real Numbers

Practice Makes Perfect Rational Numbers In the following exercises, write as the ratio of two integers.
  1. ⓐ [latex]5[/latex]
  2. ⓑ [latex]3.19[/latex]
  1. ⓐ [latex]\frac{5}{1}[/latex]
  2. ⓑ [latex]\frac{319}{100}[/latex]
  1. ⓐ [latex]8[/latex]
  2. ⓑ [latex]-1.61[/latex]
  1. ⓐ [latex]-12[/latex]
  2. ⓑ [latex]9.279[/latex]
  1. ⓐ [latex]\frac{-12}{1}[/latex]
  2. ⓑ [latex]\frac{9279}{1000}[/latex]
  1. ⓐ [latex]-16[/latex]
  2. ⓑ [latex]4.399[/latex]
In the following exercises, determine which of the given numbers are rational and which are irrational. [latex-display]0.75[/latex] , [latex]0.22\stackrel{\text{-}}{\text{3}}[/latex] , [latex]\text{1.39174\ldots }[/latex-display] Rational: [latex]0.75,0.22\stackrel{\text{-}}{\text{3}}[/latex] . Irrational: [latex]\text{1.39174\ldots }[/latex] [latex-display]0.36[/latex] , [latex]\text{0.94729\ldots }[/latex] , [latex]2.52\stackrel{\text{-}}{\text{8}}[/latex-display] [latex-display]0.\stackrel{\text{-}}{45}[/latex] , [latex]\text{1.919293\ldots }[/latex] , [latex]3.59[/latex-display] Rational: [latex]0.\stackrel{\text{-}}{45}[/latex] , [latex]3.59[/latex] . Irrational: [latex]\text{1.919293\ldots }[/latex] [latex-display]0.1\stackrel{\text{-}}{\text{3}},\text{0.42982\ldots }[/latex] , [latex]1.875[/latex-display] In the following exercises, identify whether each number is rational or irrational.
  1. ⓐ [latex]\sqrt{25}[/latex]
  2. ⓑ [latex]\sqrt{30}[/latex]
  1. ⓐ rational
  2. ⓑ irrational
  1. ⓐ [latex]\sqrt{44}[/latex]
  2. ⓑ [latex]\sqrt{49}[/latex]
  1. ⓐ [latex]\sqrt{164}[/latex]
  2. ⓑ [latex]\sqrt{169}[/latex]
  1. ⓐ irrational
  2. ⓑ rational
  1. ⓐ [latex]\sqrt{225}[/latex]
  2. ⓑ [latex]\sqrt{216}[/latex]
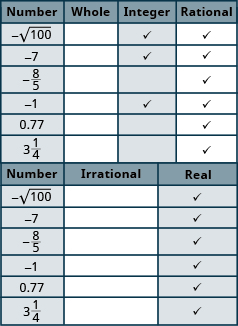
Classifying Real Numbers In the following exercises, determine whether each number is whole, integer, rational, irrational, and real. [latex-display]-8[/latex] , [latex]0,\text{1.95286....}[/latex] , [latex]\frac{12}{5}[/latex] , [latex]\sqrt{36}[/latex] , [latex]9[/latex-display] The table has seven rows and six columns. The first row is a header row that labels each column. The first column is labeled [latex-display]-9[/latex] , [latex]-3\frac{4}{9}[/latex] , [latex]-\sqrt{9}[/latex] , [latex]0.4\stackrel{\text{-}}{09}[/latex] , [latex]\frac{11}{6}[/latex] , [latex]7[/latex-display] [latex-display]-\sqrt{100}[/latex] , [latex]-7[/latex] , [latex]-\frac{8}{3}[/latex] , [latex]-1[/latex] , [latex]0.77[/latex] , [latex]3\frac{1}{4}[/latex-display] The table has seven rows and six columns. The first row is a header row that labels each column. The first column is labeled

Everyday Math

Field trip All the [latex]5\text{th}[/latex] graders at Lincoln Elementary School will go on a field trip to the science museum. Counting all the children, teachers, and chaperones, there will be [latex]147[/latex] people. Each bus holds [latex]44[/latex] people. ⓐ How many buses will be needed? ⓑ Why must the answer be a whole number? ⓒ Why shouldn't you round the answer the usual way? Child care Serena wants to open a licensed child care center. Her state requires that there be no more than [latex]12[/latex] children for each teacher. She would like her child care center to serve [latex]40[/latex] children. ⓐ How many teachers will be needed? ⓑ Why must the answer be a whole number? ⓒ Why shouldn't you round the answer the usual way? ⓐ 4 ⓑ Teachers cannot be divided ⓒ It would result in a lower number.

Writing Exercises

In your own words, explain the difference between a rational number and an irrational number. Explain how the sets of numbers (counting, whole, integer, rational, irrationals, reals) are related to each other. Answers will vary.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section. . ⓑ If most of your checks were: …confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific. …with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved? …no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need. commutative and associative properties

Practice Makes Perfect

Use the Commutative and Associative Properties In the following exercises, use the commutative properties to rewrite the given expression. [latex-display]8+9=___[/latex-display] [latex-display]7+6=___[/latex-display] 7 + 6 = 6 + 7 [latex-display]8\left(-12\right)=___[/latex-display] [latex-display]7\left(-13\right)=___[/latex-display] 7(−13) = (−13)7 [latex-display]\left(-19\right)\left(-14\right)=___[/latex-display] [latex-display]\left(-12\right)\left(-18\right)=___[/latex-display] (−12)(−18) = (−18)(−12) [latex-display]-11+8=___[/latex-display] [latex-display]-15+7=___[/latex-display] −15 + 7 = 7 + (−15) [latex-display]x+4=___[/latex-display] [latex-display]y+1=___[/latex-display] y + 1 = 1 + y [latex-display]-2a=___[/latex-display] [latex-display]-3m=___[/latex-display] −3m = m(−3) In the following exercises, use the associative properties to rewrite the given expression. [latex-display]\left(11+9\right)+14=___[/latex-display] [latex-display]\left(21+14\right)+9=___[/latex-display] (21 + 14) + 9 = 21 + (14 + 9) [latex-display]\left(12\cdot 5\right)\cdot 7=___[/latex-display] [latex-display]\left(14\cdot 6\right)\cdot 9=___[/latex-display] (14 · 6) · 9 = 14(6 · 9) [latex-display]\left(-7+9\right)+8=___[/latex-display] [latex-display]\left(-2+6\right)+7=___[/latex-display] (−2 + 6) + 7 = −2 + (6 + 7) [latex-display]\left(16\cdot \frac{4}{5}\right)\cdot 15=___[/latex-display] [latex-display]\left(13\cdot \frac{2}{3}\right)\cdot 18=___[/latex-display] [latex-display]\left(13\cdot \frac{2}{3}\right)\cdot 18=13\left(\frac{2}{3}\cdot 18\right)[/latex-display] [latex-display]3\left(4x\right)=___[/latex-display] [latex-display]4\left(7x\right)=___[/latex-display] 4(7x) = (4 · 7)x [latex-display]\left(12+x\right)+28=___[/latex-display] [latex-display]\left(17+y\right)+33=___[/latex-display] (17 + y) + 33 = 17 + (y + 33) Evaluate Expressions using the Commutative and Associative Properties In the following exercises, evaluate each expression for the given value. If [latex]y=\frac{5}{8}[/latex], evaluate: ⓐ [latex]y+0.49+\left(-y\right)[/latex] ⓑ [latex]y+\left(-y\right)+0.49[/latex] If [latex]z=\frac{7}{8}[/latex], evaluate: ⓐ [latex]z+0.97+\left(-z\right)[/latex] ⓑ [latex]z+\left(-z\right)+0.97[/latex]
  1. ⓐ 0.97
  2. ⓑ 0.97
If [latex]c=-\frac{11}{4}[/latex], evaluate: ⓐ [latex]c+3.125+\left(-c\right)[/latex] ⓑ [latex]c+\left(-c\right)+3.125[/latex] If [latex]d=-\frac{9}{4}[/latex], evaluate: ⓐ [latex]d+2.375+\left(-d\right)[/latex] ⓑ [latex]d+\left(-d\right)+2.375[/latex] ⓐ 2.375 ⓑ 2.375 If [latex]j=11[/latex], evaluate: ⓐ [latex]\frac{5}{6}\left(\frac{6}{5}j\right)[/latex] ⓑ [latex]\left(\frac{5}{6}\cdot \frac{6}{5}\right)j[/latex] If [latex]k=21[/latex], evaluate: ⓐ [latex]\frac{4}{13}\left(\frac{13}{4}k\right)[/latex] ⓑ [latex]\left(\frac{4}{13}\cdot \frac{13}{4}\right)k[/latex] ⓐ 21 ⓑ 21 If [latex]m=-25[/latex], evaluate: ⓐ [latex]-\frac{3}{7}\left(\frac{7}{3}m\right)[/latex] ⓑ [latex]\left(-\frac{3}{7}\cdot \frac{7}{3}\right)m[/latex] If [latex]n=-8[/latex], evaluate: ⓐ [latex]-\frac{5}{21}\left(\frac{21}{5}n\right)[/latex] ⓑ [latex]\left(-\frac{5}{21}\cdot \frac{21}{5}\right)n[/latex] ⓐ −8 ⓑ −8 Simplify Expressions Using the Commutative and Associative Properties In the following exercises, simplify. [latex-display]-45a+15+45a[/latex-display] [latex-display]9y+23+\left(-9y\right)[/latex-display] 23 [latex-display]\frac{1}{2}+\frac{7}{8}+\left(-\frac{1}{2}\right)[/latex-display] [latex-display]\frac{2}{5}+\frac{5}{12}+\left(-\frac{2}{5}\right)[/latex-display] [latex-display]\frac{5}{12}[/latex-display] [latex-display]\frac{3}{20}\cdot \frac{49}{11}\cdot \frac{20}{3}[/latex-display] [latex-display]\frac{13}{18}\cdot \frac{25}{7}\cdot \frac{18}{13}[/latex-display] [latex-display]\frac{25}{7}[/latex-display] [latex-display]\frac{7}{12}\cdot \frac{9}{17}\cdot \frac{24}{7}[/latex-display] [latex-display]\frac{3}{10}\cdot \frac{13}{23}\cdot \frac{50}{3}[/latex-display] [latex-display]\frac{65}{23}[/latex-display] [latex-display]-24\cdot 7\cdot \frac{3}{8}[/latex-display] [latex-display]-36\cdot 11\cdot \frac{4}{9}[/latex-display] −176 [latex-display]\left(\frac{5}{6}+\frac{8}{15}\right)+\frac{7}{15}[/latex-display] [latex-display]\left(\frac{1}{12}+\frac{4}{9}\right)+\frac{5}{9}[/latex-display] [latex-display]\frac{13}{12}[/latex-display] [latex-display]\frac{5}{13}+\frac{3}{4}+\frac{1}{4}[/latex-display] [latex-display]\frac{8}{15}+\frac{5}{7}+\frac{2}{7}[/latex-display] [latex-display]\frac{23}{15}[/latex-display] [latex-display]\left(4.33p+1.09p\right)+3.91p[/latex-display] [latex-display]\left(5.89d+2.75d\right)+1.25d[/latex-display] 9.89d [latex-display]17\left(0.25\right)\left(4\right)[/latex-display] [latex-display]36\left(0.2\right)\left(5\right)[/latex-display] 36 [latex-display]\left[2.48\left(12\right)\right]\left(0.5\right)[/latex-display] [latex-display]\left[9.731\left(4\right)\right]\left(0.75\right)[/latex-display] 29.193 [latex-display]7\left(4a\right)[/latex-display] [latex-display]9\left(8w\right)[/latex-display] 72w [latex-display]-15\left(5m\right)[/latex-display] [latex-display]-23\left(2n\right)[/latex-display] −46n [latex-display]12\left(\frac{5}{6}p\right)[/latex-display] [latex-display]20\left(\frac{3}{5}q\right)[/latex-display] 12q [latex-display]14x+19y+25x+3y[/latex-display] [latex-display]15u+11v+27u+19v[/latex-display] 42u + 30v [latex-display]43m+\left(-12n\right)+\text{ }\left(-16m\right)+\left(-9n\right)[/latex-display] [latex-display]-22p+17q+\left(-35p\right)+\left(-27q\right)[/latex-display] −57p + (−10q) [latex-display]\frac{3}{8}g+\frac{1}{12}h+\frac{7}{8}g+\frac{5}{12}h[/latex-display] [latex-display]\frac{5}{6}a+\frac{3}{10}b+\frac{1}{6}a+\frac{9}{10}b[/latex-display] [latex-display]a+\frac{6}{5}b[/latex-display] [latex-display]6.8p+9.14q+\left(-4.37p\right)+\left(-0.88q\right)[/latex-display] [latex-display]9.6m+7.22n+\left(-2.19m\right)+\left(-0.65n\right)[/latex-display] 7.41m + 6.57n

Everyday Math

Stamps Allie and Loren need to buy stamps. Allie needs four [latex]\text{$0.49}[/latex] stamps and nine [latex]\text{$0.02}[/latex] stamps. Loren needs eight [latex]\text{$0.49}[/latex] stamps and three [latex]\text{$0.02}[/latex] stamps. ⓐ How much will Allie’s stamps cost? ⓑ How much will Loren’s stamps cost? ⓒ What is the total cost of the girls’ stamps? ⓓ How many [latex]\text{$0.49}[/latex] stamps do the girls need altogether? How much will they cost? ⓔ How many [latex]\text{$0.02}[/latex] stamps do the girls need altogether? How much will they cost? Counting Cash Grant is totaling up the cash from a fundraising dinner. In one envelope, he has twenty-three [latex]\text{$5}[/latex] bills, eighteen [latex]\text{$10}[/latex] bills, and thirty-four [latex]\text{$20}[/latex] bills. In another envelope, he has fourteen [latex]\text{$5}[/latex] bills, nine [latex]\text{$10}[/latex] bills, and twenty-seven [latex]\text{$20}[/latex] bills. ⓐ How much money is in the first envelope? ⓑ How much money is in the second envelope? ⓒ What is the total value of all the cash? ⓓ What is the value of all the [latex]\text{$5}[/latex] bills? ⓔ What is the value of all [latex]\text{$10}[/latex] bills? ⓕ What is the value of all [latex]\text{$20}[/latex] bills?
  1. ⓐ $975
  2. ⓑ $700
  3. ⓒ $1675
  4. ⓓ $185
  5. ⓔ $270
  6. ⓕ $1220

Writing Exercises

In your own words, state the Commutative Property of Addition and explain why it is useful. In your own words, state the Associative Property of Multiplication and explain why it is useful. Answers will vary.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section. . ⓑ After reviewing this checklist, what will you do to become confident for all objectives?   Practice Makes Perfect Simplify Expressions Using the Distributive Property In the following exercises, simplify using the distributive property. [latex-display]4\left(x+8\right)[/latex-display] [latex-display]3\left(a+9\right)[/latex-display] 3a + 27 [latex-display]8\left(4y+9\right)[/latex-display] [latex-display]9\left(3w+7\right)[/latex-display] 27w + 63 [latex-display]6\left(c - 13\right)[/latex-display] [latex-display]7\left(y - 13\right)[/latex-display] 7y − 91 [latex-display]7\left(3p - 8\right)[/latex-display] [latex-display]5\left(7u - 4\right)[/latex-display] 35u − 20 [latex-display]\frac{1}{2}\left(n+8\right)[/latex-display] [latex-display]\frac{1}{3}\left(u+9\right)[/latex-display] [latex-display]\frac{1}{3}u+3[/latex-display] [latex-display]\frac{1}{4}\left(3q+12\right)[/latex-display] [latex-display]\frac{1}{5}\left(4m+20\right)[/latex-display] [latex-display]\frac{4}{5}m+4[/latex-display] [latex-display]9\left(\frac{5}{9}y-\frac{1}{3}\right)[/latex-display] [latex-display]10\left(\frac{3}{10}x-\frac{2}{5}\right)[/latex-display] 3x − 4 [latex-display]12\left(\frac{1}{4}+\frac{2}{3}r\right)[/latex-display] [latex-display]12\left(\frac{1}{6}+\frac{3}{4}s\right)[/latex-display] 2 + 9s [latex-display]r\left(s - 18\right)[/latex-display] [latex-display]u\left(v - 10\right)[/latex-display] uv − 10u [latex-display]\left(y+4\right)p[/latex-display] [latex-display]\left(a+7\right)x[/latex-display] ax + 7x [latex-display]-2\left(y+13\right)[/latex-display] [latex-display]-3\left(a+11\right)[/latex-display] −3a − 33 [latex-display]-7\left(4p+1\right)[/latex-display] [latex-display]-9\left(9a+4\right)[/latex-display] −81a − 36 [latex-display]-3\left(x - 6\right)[/latex-display] [latex-display]-4\left(q - 7\right)[/latex-display] −4q + 28 [latex-display]-9\left(3a - 7\right)[/latex-display] [latex-display]-6\left(7x - 8\right)[/latex-display] −42x + 48 [latex-display]-\left(r+7\right)[/latex-display] [latex-display]-\left(q+11\right)[/latex-display] −q − 11 [latex-display]-\left(3x - 7\right)[/latex-display] [latex-display]-\left(5p - 4\right)[/latex-display] −5p + 4 [latex-display]5+9\left(n - 6\right)[/latex-display] [latex-display]12+8\left(u - 1\right)[/latex-display] 8u + 4 [latex-display]16 - 3\left(y+8\right)[/latex-display] [latex-display]18 - 4\left(x+2\right)[/latex-display] −4x + 10 [latex-display]4 - 11\left(3c - 2\right)[/latex-display] [latex-display]9 - 6\left(7n - 5\right)[/latex-display] −42n + 39 [latex-display]22-\left(a+3\right)[/latex-display] [latex-display]8-\left(r - 7\right)[/latex-display] −r + 15 [latex-display]-12-\left(u+10\right)[/latex-display] [latex-display]-4-\left(c - 10\right)[/latex-display] −c + 6 [latex-display]\left(5m - 3\right)-\left(m+7\right)[/latex-display] [latex-display]\left(4y - 1\right)-\left(y - 2\right)[/latex-display] 3y + 1 [latex-display]5\left(2n+9\right)+12\left(n - 3\right)[/latex-display] [latex-display]9\left(5u+8\right)+2\left(u - 6\right)[/latex-display] 47u + 60 [latex-display]9\left(8x - 3\right)-\left(-2\right)[/latex-display] [latex-display]4\left(6x - 1\right)-\left(-8\right)[/latex-display] 24x + 4 [latex-display]14\left(c - 1\right)-8\left(c - 6\right)[/latex-display] [latex-display]11\left(n - 7\right)-5\left(n - 1\right)[/latex-display] 6n − 72 [latex-display]6\left(7y+8\right)-\left(30y - 15\right)[/latex-display] [latex-display]7\left(3n+9\right)-\left(4n - 13\right)[/latex-display] 17n + 76 Evaluate Expressions Using the Distributive Property In the following exercises, evaluate both expressions for the given value. If [latex]v=-2[/latex], evaluate ⓐ [latex]6\left(4v+7\right)[/latex] ⓑ [latex]6\cdot 4v+6\cdot 7[/latex] If [latex]u=-1[/latex], evaluate ⓐ [latex]8\left(5u+12\right)[/latex] ⓑ [latex]8\cdot 5u+8\cdot 12[/latex] ⓐ 56 ⓑ 56 If [latex]n=\frac{2}{3}[/latex], evaluate ⓐ [latex]3\left(n+\frac{5}{6}\right)[/latex] ⓑ [latex]3\cdot n+3\cdot \frac{5}{6}[/latex] If [latex]y=\frac{3}{4}[/latex], evaluate ⓐ [latex]4\left(y+\frac{3}{8}\right)[/latex] ⓑ [latex]4\cdot y+4\cdot \frac{3}{8}[/latex] ⓐ [latex]\frac{9}{2}[/latex] ⓑ [latex]\frac{9}{2}[/latex] If [latex]y=\frac{7}{12}[/latex], evaluate ⓐ [latex]-3\left(4y+15\right)[/latex] ⓑ [latex]3\cdot 4y+\left(-3\right)\cdot 15[/latex] If [latex]p=\frac{23}{30}[/latex], evaluate ⓐ [latex]-6\left(5p+11\right)[/latex] ⓑ [latex]-6\cdot 5p+\left(-6\right)\cdot 11[/latex] ⓐ −89 ⓑ −89 If [latex]m=0.4[/latex], evaluate ⓐ [latex]-10\left(3m - 0.9\right)[/latex] ⓑ [latex]-10\cdot 3m-\left(-10\right)\left(0.9\right)[/latex] If [latex]n=0.75[/latex], evaluate ⓐ [latex]-100\left(5n+1.5\right)[/latex] ⓑ [latex]-100\cdot 5n+\left(-100\right)\left(1.5\right)[/latex] ⓐ −525 ⓑ −525 If [latex]y=-25[/latex], evaluate ⓐ [latex]-\left(y - 25\right)[/latex] ⓑ [latex]-y+25[/latex] If [latex]w=-80[/latex], evaluate ⓐ [latex]-\left(w - 80\right)[/latex] ⓑ [latex]-w+80[/latex] ⓐ 160 ⓑ 160 If [latex]p=0.19[/latex], evaluate ⓐ [latex]-\left(p+0.72\right)[/latex] ⓑ [latex]-p - 0.72[/latex] If [latex]q=0.55[/latex], evaluate ⓐ [latex]-\left(q+0.48\right)[/latex] ⓑ [latex]-q - 0.48[/latex] ⓐ −1.03 ⓑ −1.03

Everyday Math

Buying by the case Joe can buy his favorite ice tea at a convenience store for [latex]\text{$1.99}[/latex] per bottle. At the grocery store, he can buy a case of [latex]12[/latex] bottles for [latex]\text{$23.88}[/latex]. ⓐ Use the distributive property to find the cost of [latex]12[/latex] bottles bought individually at the convenience store. (Hint: notice that [latex]\text{$1.99}[/latex] is [latex]\text{$2}-\text{$0.01}[/latex]. ) ⓑ Is it a bargain to buy the iced tea at the grocery store by the case? Multi-pack purchase Adele’s shampoo sells for [latex]\text{$3.97}[/latex] per bottle at the drug store. At the warehouse store, the same shampoo is sold as a [latex]\text{3-pack}[/latex] for [latex]\text{$10.49}[/latex]. ⓐ Show how you can use the distributive property to find the cost of [latex]3[/latex] bottles bought individually at the drug store. ⓑ How much would Adele save by buying the [latex]\text{3-pack}[/latex] at the warehouse store? ⓐ 3(4 − 0.03) = 11.91 ⓑ $1.42

Writing Exercises

Simplify [latex]8\left(x-\frac{1}{4}\right)[/latex] using the distributive property and explain each step. Explain how you can multiply [latex]4\left(\text{$5.97}\right)[/latex] without paper or a calculator by thinking of [latex]\text{$5.97}[/latex] as [latex]6 - 0.03[/latex] and then using the distributive property.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section. . ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?  

Practice Makes Perfect

Recognize the Identity Properties of Addition and Multiplication In the following exercises, identify whether each example is using the identity property of addition or multiplication. [latex-display]101+0=101[/latex-display] [latex-display]\frac{3}{5}\left(1\right)=\frac{3}{5}[/latex-display] identity property of multiplication [latex-display]-9\cdot 1=-9[/latex-display] [latex-display]0+64=64[/latex-display] identity property of addition Use the Inverse Properties of Addition and Multiplication In the following exercises, find the multiplicative inverse. [latex-display]8[/latex-display] [latex-display]14[/latex-display] [latex-display]\frac{1}{14}[/latex-display] [latex-display]-17[/latex-display] [latex-display]-19[/latex-display] [latex-display]-\frac{1}{19}[/latex-display] [latex-display]\frac{7}{12}[/latex-display] [latex-display]\frac{8}{13}[/latex-display] [latex-display]\frac{13}{8}[/latex-display] [latex-display]-\frac{3}{10}[/latex-display] [latex-display]-\frac{5}{12}[/latex-display] [latex-display]-\frac{12}{5}[/latex-display] [latex-display]0.8[/latex-display] [latex-display]0.4[/latex-display] [latex-display]\frac{5}{2}[/latex-display] [latex-display]-0.2[/latex-display] [latex-display]-0.5[/latex-display] −2 Use the Properties of Zero In the following exercises, simplify using the properties of zero. [latex-display]48\cdot 0[/latex-display] [latex-display]\frac{0}{6}[/latex-display] 0 [latex-display]\frac{3}{0}[/latex-display] [latex-display]22\cdot 0[/latex-display] 0 [latex-display]0\div \frac{11}{12}[/latex-display] [latex-display]\frac{6}{0}[/latex-display] undefined [latex-display]\frac{0}{3}[/latex-display] [latex-display]0\div \frac{7}{15}[/latex-display] 0 [latex-display]0\cdot \frac{8}{15}[/latex-display] [latex-display]\left(-3.14\right)\left(0\right)[/latex-display] 0 [latex-display]5.72\div 0[/latex-display] [latex-display]\frac{\frac{1}{10}}{0}[/latex-display] undefined Simplify Expressions using the Properties of Identities, Inverses, and Zero In the following exercises, simplify using the properties of identities, inverses, and zero. [latex-display]19a+44 - 19a[/latex-display] [latex-display]27c+16 - 27c[/latex-display] 16 [latex-display]38+11r - 38[/latex-display] [latex-display]92+31s - 92[/latex-display] 31s [latex-display]10\left(0.1d\right)[/latex-display] [latex-display]100\left(0.01p\right)[/latex-display] p [latex-display]5\left(0.6q\right)[/latex-display] [latex-display]40\left(0.05n\right)[/latex-display] 2n [latex-display]\frac{0}{r+20}[/latex] , where [latex]r\ne -20[/latex-display] [latex-display]\frac{0}{s+13}[/latex] , where [latex]s\ne -13[/latex-display] 0 [latex-display]\frac{0}{u - 4.99}[/latex] , where [latex]u\ne 4.99[/latex-display] [latex-display]\frac{0}{v - 65.1}[/latex] , where [latex]v\ne 65.1[/latex-display] 0 [latex-display]0\div \left(x-\frac{1}{2}\right)[/latex] , where [latex]x\ne \frac{1}{2}[/latex-display] [latex-display]0\div \left(y-\frac{1}{6}\right)[/latex] , where [latex]y\ne \frac{1}{6}[/latex-display] 0 [latex-display]\frac{32 - 5a}{0}[/latex] , where [latex]32 - 5a\ne 0[/latex-display] [latex-display]\frac{28 - 9b}{0}[/latex] , where [latex]28 - 9b\ne 0[/latex-display] undefined [latex-display]\frac{2.1+0.4c}{0}[/latex] , where [latex]2.1+0.4c\ne 0[/latex-display] [latex-display]\frac{1.75+9f}{0}[/latex] , where [latex]1.75+9f\ne 0[/latex-display] undefined [latex-display]\left(\frac{3}{4}+\frac{9}{10}m\right)\div 0[/latex] , where [latex]\frac{3}{4}+\frac{9}{10}m\ne 0[/latex-display] [latex-display]\left(\frac{5}{16}n-\frac{3}{7}\right)\div 0[/latex] , where [latex]\frac{5}{16}n-\frac{3}{7}\ne 0[/latex-display] undefined [latex-display]\frac{9}{10}\cdot \frac{10}{9}\left(18p - 21\right)[/latex-display] [latex-display]\frac{5}{7}\cdot \frac{7}{5}\left(20q - 35\right)[/latex-display] 20q − 35 [latex-display]15\cdot \frac{3}{5}\left(4d+10\right)[/latex-display] [latex-display]18\cdot \frac{5}{6}\left(15h+24\right)[/latex-display] 225h + 360

Everyday Math

Insurance copayment Carrie had to have [latex]5[/latex] fillings done. Each filling cost [latex]\text{$80}[/latex]. Her dental insurance required her to pay [latex]20%[/latex] of the cost. Calculate Carrie’s cost ⓐ by finding her copay for each filling, then finding her total cost for [latex]5[/latex] fillings, and ⓑ by multiplying [latex]5\left(0.20\right)\left(80\right)[/latex]. ⓒ Which of the Properties of Real Numbers did you use for part (b)? Cooking time Helen bought a [latex]\text{24-pound}[/latex] turkey for her family’s Thanksgiving dinner and wants to know what time to put the turkey in the oven. She wants to allow [latex]20[/latex] minutes per pound cooking time. ⓐ Calculate the length of time needed to roast the turkey by multiplying [latex]24\cdot 20[/latex] to find the number of minutes and then multiplying the product by [latex]\frac{1}{60}[/latex] to convert minutes into hours. ⓑ Multiply [latex]24\left(20\cdot \frac{1}{60}\right)[/latex]. ⓒ Which of the Properties of Real Numbers allows you to multiply [latex]24\left(20\cdot \frac{1}{60}\right)[/latex] instead of [latex]\left(24\cdot 20\right)\frac{1}{60}?[/latex] ⓐ 8 hours ⓑ 8 ⓒ associative property of multiplication

Writing Exercises

In your own words, describe the difference between the additive inverse and the multiplicative inverse of a number. How can the use of the properties of real numbers make it easier to simplify expressions? Answers will vary.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.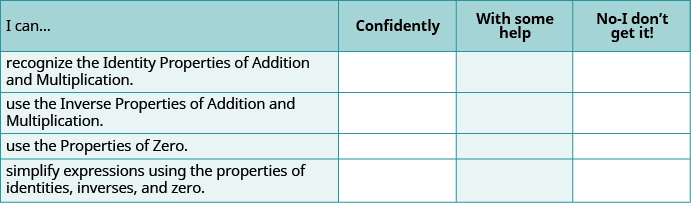 . ⓑ On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Practice Makes Perfect

Determine Whether a Number is a Solution of an Equation In the following exercises, determine whether each number is a solution of the given equation. [latex-display]4x - 2=6[/latex-display] ⓐ [latex]x=-2[/latex] ⓑ [latex]x=-1[/latex] ⓒ [latex]x=2[/latex]
  1. ⓐ no
  2. ⓑ yes
  3. ⓒ no
[latex-display]4y - 10=-14[/latex-display] ⓐ [latex]y=-6[/latex] ⓑ [latex]y=-1[/latex] ⓒ [latex]y=1[/latex] [latex-display]9a+27=-63[/latex-display] ⓐ [latex]a=6[/latex] ⓑ [latex]a=-6[/latex] ⓒ [latex]a=-10[/latex]
  1. ⓐ no
  2. ⓑ no
  3. ⓒ yes
[latex-display]7c+42=-56[/latex-display] ⓐ [latex]c=2[/latex] ⓑ [latex]c=-2[/latex] ⓒ [latex]c=-14[/latex] Solve Equations Using the Addition and Subtraction Properties of Equality In the following exercises, solve for the unknown. [latex-display]n+12=5[/latex-display] −7 [latex-display]m+16=2[/latex-display] [latex-display]p+9=-8[/latex-display] −17 [latex-display]q+5=-6[/latex-display] [latex-display]u - 3=-7[/latex-display] −4 [latex-display]v - 7=-8[/latex-display] [latex-display]h - 10=-4[/latex-display] 6 [latex-display]k - 9=-5[/latex-display] [latex-display]x+\left(-2\right)=-18[/latex-display] −16 [latex-display]y+\left(-3\right)=-10[/latex-display] [latex-display]r-\left(-5\right)=-9[/latex-display] −14 [latex-display]s-\left(-2\right)=-11[/latex-display] Model the Division Property of Equality In the following exercises, write the equation modeled by the envelopes and counters and then solve it. 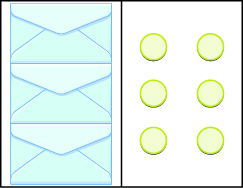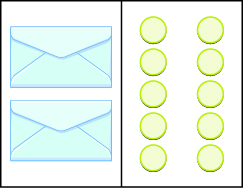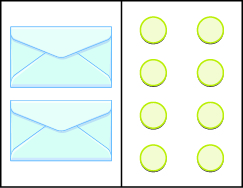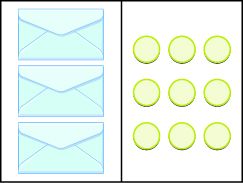No Alt Text 3x = 6; x = 2 No Alt Text No Alt Text 2x = 8; x = 4 No Alt Text Solve Equations Using the Division Property of Equality In the following exercises, solve each equation using the division property of equality and check the solution. [latex-display]5x=45[/latex-display] 9 [latex-display]4p=64[/latex-display] [latex-display]-7c=56[/latex-display] −8 [latex-display]-9x=54[/latex-display] [latex-display]-14p=-42[/latex-display] 3 [latex-display]-8m=-40[/latex-display] [latex-display]-120=10q[/latex-display] −12 [latex-display]-75=15y[/latex-display] [latex-display]24x=480[/latex-display] 20 [latex-display]18n=540[/latex-display] [latex-display]-3z=0[/latex-display] 0 [latex-display]4u=0[/latex-display] Translate to an Equation and Solve In the following exercises, translate and solve. Four more than [latex]n[/latex] is equal to 1. n + 4 = 1; n = −3 Nine more than [latex]m[/latex] is equal to 5. The sum of eight and [latex]p[/latex] is [latex]-3[/latex] . 8 + p = −3; p = −11 The sum of two and [latex]q[/latex] is [latex]-7[/latex] . The difference of [latex]a[/latex] and three is [latex]-14[/latex] . a − 3 = −14; a = −11 The difference of [latex]b[/latex] and [latex]5[/latex] is [latex]-2[/latex] . The number −42 is the product of −7 and [latex]x[/latex] . −42 = −7x; x = 6 The number −54 is the product of −9 and [latex]y[/latex] . The product of [latex]f[/latex] and −15 is 75. f(−15) = 75; f = 5 The product of [latex]g[/latex] and −18 is 36. −6 plus [latex]c[/latex] is equal to 4. −6 + c = 4; c = 10 −2 plus [latex]d[/latex] is equal to 1. Nine less than [latex]n[/latex] is −4. m − 9 = −4; m = 5 Thirteen less than [latex]n[/latex] is [latex]-10[/latex] . Mixed Practice In the following exercises, solve.
  1. ⓐ [latex]x+2=10[/latex]
  2. ⓑ [latex]2x=10[/latex]
  1. ⓐ 8
  2. ⓑ 5
  1. ⓐ [latex]y+6=12[/latex]
  2. ⓑ [latex]6y=12[/latex]
  1. ⓐ [latex]-3p=27[/latex]
  2. ⓑ [latex]p - 3=27[/latex]
  1. ⓐ −9
  2. ⓑ 30
  1. ⓐ [latex]-2q=34[/latex]
  2. ⓑ [latex]q - 2=34[/latex]
[latex-display]a - 4=16[/latex-display] 20 [latex-display]b - 1=11[/latex-display] [latex-display]-8m=-56[/latex-display] 7 [latex-display]-6n=-48[/latex-display] [latex-display]-39=u+13[/latex-display] −52 [latex-display]-100=v+25[/latex-display] [latex-display]11r=-99[/latex-display] −9 [latex-display]15s=-300[/latex-display] [latex-display]100=20d[/latex-display] 5 [latex-display]250=25n[/latex-display] [latex-display]-49=x - 7[/latex-display] −42 [latex-display]64=y - 4[/latex-display]

Everyday Math

Cookie packaging A package of [latex]\text{51 cookies}[/latex] has [latex]3[/latex] equal rows of cookies. Find the number of cookies in each row, [latex]c[/latex], by solving the equation [latex]3c=51[/latex]. 17 cookies Kindergarten class Connie’s kindergarten class has [latex]\text{24 children.}[/latex] She wants them to get into [latex]4[/latex] equal groups. Find the number of children in each group, [latex]g[/latex], by solving the equation [latex]4g=24[/latex].

Writing Exercises

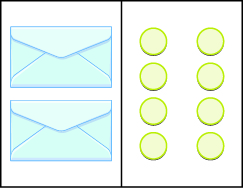
Is modeling the Division Property of Equality with envelopes and counters helpful to understanding how to solve the equation [latex]3x=15?[/latex] Explain why or why not. Sample answer: It is helpful because it shows how the counters can be divided among the envelopes. Suppose you are using envelopes and counters to model solving the equations [latex]x+4=12[/latex] and [latex]4x=12[/latex]. Explain how you would solve each equation. Frida started to solve the equation [latex]-3x=36[/latex] by adding [latex]3[/latex] to both sides. Explain why Frida’s method will not solve the equation. Sample answer: The operation used in the equation is multiplication. The inverse of multiplication is division, not addition. Raoul started to solve the equation [latex]4y=40[/latex] by subtracting [latex]4[/latex] from both sides. Explain why Raoul’s method will not solve the equation.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section. . ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?

Chapter Review Exercises

Introduction to Integers Locate Positive and Negative Numbers on the Number Line In the following exercises, locate and label the integer on the number line. [latex-display]5[/latex-display] This figure is a number line. It is scaled from negative 10 to 10 in increments of 2. There is a point at 5. [latex-display]-5[/latex-display] [latex-display]-3[/latex-display] This figure is a number line. It is scaled from negative 10 to 10 in increments of 2. There is a point at negative 3. [latex-display]3[/latex-display] [latex-display]-8[/latex-display] This figure is a number line. It is scaled from negative 10 to 10 in increments of 2. There is a point at negative 8. [latex-display]-7[/latex-display] Order Positive and Negative Numbers In the following exercises, order each of the following pairs of numbers, using [latex]<[/latex]; or [latex]\text{>.}[/latex] [latex-display]4\text{__}8[/latex-display] < [latex-display]-6\text{__}3[/latex-display] [latex-display]-5\text{__}-10[/latex-display] > [latex-display]-9\text{__}-4[/latex-display] [latex-display]2\text{__}-7[/latex-display] > [latex-display]-3\text{__}1[/latex-display] Find Opposites In the following exercises, find the opposite of each number. [latex-display]6[/latex-display] −6 [latex-display]-2[/latex-display] [latex-display]-4[/latex-display] 4 [latex-display]3[/latex-display] In the following exercises, simplify.
  1. ⓐ [latex]-\left(8\right)[/latex]
  2. ⓑ [latex]-\left(-8\right)[/latex]
  1. ⓐ −8
  2. ⓑ 8
  1. ⓐ [latex]-\left(9\right)[/latex]
  2. ⓑ [latex]-\left(-9\right)[/latex]
In the following exercises, evaluate. [latex-display]-x,\text{when}[/latex-display] ⓐ [latex]x=32[/latex] ⓑ [latex]x=-32[/latex]
  1. ⓐ −32
  2. ⓑ 32
[latex-display]-n,\text{when}[/latex-display] ⓐ [latex]n=20[/latex] ⓐ [latex]n=-20[/latex] Simplify Absolute Values In the following exercises, simplify. [latex-display]|-21|[/latex-display] 21 [latex-display]|-42|[/latex-display] [latex-display]|36|[/latex-display] 36 [latex-display]-|15|[/latex-display] [latex-display]|0|[/latex-display] 0 [latex-display]-|-75|[/latex-display] In the following exercises, evaluate. [latex-display]|x|\text{when}x=-14[/latex-display] 14 [latex-display]-|r|\text{when}r=27[/latex-display] [latex-display]-|-y|\text{when}y=33[/latex-display] −33 [latex-display]|{\text{-n}}|\text{when}n=-4[/latex-display] In the following exercises, fill in [latex]\text{<},\text{>},\text{or}=[/latex] for each of the following pairs of numbers. [latex-display]-|-4|\text{__}4[/latex-display] < [latex-display]-2\text{__}|-2|[/latex-display] [latex-display]-|-6|\text{__}-6[/latex-display] = [latex-display]-|-9|\text{__}|-9|[/latex-display] In the following exercises, simplify. [latex-display]-\left(-55\right)\text{and}-|-55|[/latex-display] −55; −55 [latex-display]-\left(-48\right)\text{and}-|-48|[/latex-display] [latex-display]|12 - 5|[/latex-display] 7 [latex-display]|9+7|[/latex-display] [latex-display]6|-9|[/latex-display] 54 [latex-display]|14 - 8|-|-2|[/latex-display] [latex-display]|9 - 3|-|5 - 12|[/latex-display] −1 [latex-display]5+4|15 - 3|[/latex-display] Translate Phrases to Expressions with Integers In the following exercises, translate each of the following phrases into expressions with positive or negative numbers. the opposite of [latex]16[/latex] −16 the opposite of [latex]-8[/latex] negative [latex]3[/latex] −3 [latex-display]19[/latex] minus negative [latex]12[/latex-display] a temperature of [latex]10[/latex] below zero −10° an elevation of [latex]\text{85 feet}[/latex] below sea level Add Integers Model Addition of Integers In the following exercises, model the following to find the sum. [latex-display]3+7[/latex-display] 10 [latex-display]-2+6[/latex-display] [latex-display]5+\left(-4\right)[/latex-display] 1 [latex-display]-3+\left(-6\right)[/latex-display] Simplify Expressions with Integers In the following exercises, simplify each expression. [latex-display]14+82[/latex-display] 96 [latex-display]-33+\left(-67\right)[/latex-display] [latex-display]-75+25[/latex-display] −50 [latex-display]54+\left(-28\right)[/latex-display] [latex-display]11+\left(-15\right)+3[/latex-display] −1 [latex-display]-19+\left(-42\right)+12[/latex-display] [latex-display]-3+6\left(-1+5\right)[/latex-display] 21 [latex-display]10+4\left(-3+7\right)[/latex-display] Evaluate Variable Expressions with Integers In the following exercises, evaluate each expression. [latex-display]n+4\text{when}[/latex-display] ⓐ [latex]n=-1[/latex] ⓑ [latex]n=-20[/latex]
  1. ⓐ 3
  2. ⓑ −16
[latex-display]x+\left(-9\right)\text{when}[/latex-display] ⓐ [latex]x=3[/latex] ⓑ [latex]x=-3[/latex] [latex-display]{\left(x+y\right)}^{3}\text{when}x=-4,y=1[/latex-display] −27 [latex-display]{\left(u+v\right)}^{2}\text{when}u=-4,v=11[/latex-display] Translate Word Phrases to Algebraic Expressions In the following exercises, translate each phrase into an algebraic expression and then simplify. [latex-display]\text{the sum of -8 and 2}[/latex-display] −8 + 2 = −6 [latex-display]\text{4 more than -12}[/latex-display] [latex-display]\text{10 more than the sum of -5 and -6}[/latex-display] 10 + [−5 + (−6)] = −1 [latex-display]\text{the sum of}3\text{and}-5,\text{increased by 18}[/latex-display] Add Integers in Applications In the following exercises, solve. Temperature On Monday, the high temperature in Denver was [latex]\text{-4 degrees.}[/latex] Tuesday’s high temperature was [latex]\text{20 degrees}[/latex] more. What was the high temperature on Tuesday? 16 degrees Credit Frida owed [latex]\text{$75}[/latex] on her credit card. Then she charged [latex]\text{$21}[/latex] more. What was her new balance? Subtract Integers Model Subtraction of Integers In the following exercises, model the following. [latex-display]6 - 1[/latex-display] This figure is a row of 6 light pink circles, representing positive counters. The first one is circled. 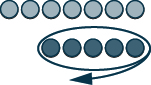5 [latex-display]-4-\left(-3\right)[/latex-display] [latex-display]2-\left(-5\right)[/latex-display] This figure shows 2 rows. The first row shows 7 light pink circles, representing positive counters. The second row shows 5 dark pink circles, representing negative counters. The entire second row is circled. 7 [latex-display]-1 - 4[/latex-display] Simplify Expressions with Integers In the following exercises, simplify each expression. [latex-display]24 - 16[/latex-display] 8 [latex-display]19-\left(-9\right)[/latex-display] [latex-display]-31 - 7[/latex-display] −38 [latex-display]-40-\left(-11\right)[/latex-display] [latex-display]-52-\left(-17\right)-23[/latex-display] −58 [latex-display]25-\left(-3 - 9\right)[/latex-display] [latex-display]\left(1 - 7\right)-\left(3 - 8\right)[/latex-display] −1 [latex-display]{3}^{2}-{7}^{2}[/latex-display] Evaluate Variable Expressions with Integers In the following exercises, evaluate each expression. [latex-display]x - 7\text{when}[/latex-display] ⓐ [latex]x=5[/latex] ⓑ [latex]x=-4[/latex]
  1. ⓐ −2
  2. ⓑ −11
[latex-display]10-y\text{when}[/latex-display] ⓐ [latex]y=15[/latex] ⓑ [latex]y=-16[/latex] [latex-display]2{n}^{2}-n+5\text{when}n=-4[/latex-display] 41 [latex-display]-15 - 3{u}^{2}\text{when}u=-5[/latex-display] Translate Phrases to Algebraic Expressions In the following exercises, translate each phrase into an algebraic expression and then simplify. the difference of [latex]-12\text{and}5[/latex] −12 − 5 = −17 subtract [latex]23[/latex] from [latex]-50[/latex] Subtract Integers in Applications In the following exercises, solve the given applications. Temperature One morning the temperature in Bangor, Maine was [latex]\text{18 degrees.}[/latex] By afternoon, it had dropped [latex]\text{20 degrees.}[/latex] What was the afternoon temperature? −2 degrees Temperature On January 4, the high temperature in Laredo, Texas was [latex]\text{78 degrees,}[/latex] and the high in Houlton, Maine was [latex]-28\text{degrees}[/latex]. What was the difference in temperature of Laredo and Houlton? Multiply and Divide Integers Multiply Integers In the following exercises, multiply. [latex-display]-9\cdot 4[/latex-display] −36 [latex-display]5\left(-7\right)[/latex-display] [latex-display]\left(-11\right)\left(-11\right)[/latex-display] 121 [latex-display]-1\cdot 6[/latex-display] Divide Integers In the following exercises, divide. [latex-display]56\div \left(-8\right)[/latex-display] −7 [latex-display]-120\div \left(-6\right)[/latex-display] [latex-display]-96\div 12[/latex-display] −8 [latex-display]96\div \left(-16\right)[/latex-display] [latex-display]45\div \left(-1\right)[/latex-display] −45 [latex-display]-162\div \left(-1\right)[/latex-display] Simplify Expressions with Integers In the following exercises, simplify each expression. [latex-display]5\left(-9\right)-3\left(-12\right)[/latex-display] −9 [latex-display]{\left(-2\right)}^{5}[/latex-display] [latex-display]-{3}^{4}[/latex-display] −81 [latex-display]\left(-3\right)\left(4\right)\left(-5\right)\left(-6\right)[/latex-display] [latex-display]42 - 4\left(6 - 9\right)[/latex-display] 54 [latex-display]\left(8 - 15\right)\left(9 - 3\right)[/latex-display] [latex-display]-2\left(-18\right)\div 9[/latex-display] 4 [latex-display]45\div \left(-3\right)-12[/latex-display] Evaluate Variable Expressions with Integers In the following exercises, evaluate each expression. [latex-display]7x - 3\text{when}x=-9[/latex-display] −66 [latex-display]16 - 2n\text{when}n=-8[/latex-display] [latex-display]5a+8b\text{when}a=-2,b=-6[/latex-display] −58 [latex-display]{x}^{2}+5x+4\text{when}x=-3[/latex-display] Translate Word Phrases to Algebraic Expressions In the following exercises, translate to an algebraic expression and simplify if possible. the product of [latex]-12[/latex] and [latex]6[/latex] −12(6) = −72 the quotient of [latex]3[/latex] and the sum of [latex]-7[/latex] and [latex]s[/latex] Solve Equations using Integers; The Division Property of Equality Determine Whether a Number is a Solution of an Equation In the following exercises, determine whether each number is a solution of the given equation. [latex-display]5x - 10=-35[/latex-display] ⓐ [latex]x=-9[/latex] ⓑ [latex]x=-5[/latex] ⓒ [latex]x=5[/latex]
  1. ⓐ no
  2. ⓑ yes
  3. ⓒ no
[latex-display]8u+24=-32[/latex-display] ⓐ [latex]u=-7[/latex] ⓑ [latex]u=-1[/latex] ⓒ [latex]u=7[/latex] Using the Addition and Subtraction Properties of Equality In the following exercises, solve. [latex-display]a+14=2[/latex-display] −12 [latex-display]b - 9=-15[/latex-display] −6 [latex-display]c+\left(-10\right)=-17[/latex-display] −7 [latex-display]d-\left(-6\right)=-26[/latex-display] −32 Model the Division Property of Equality In the following exercises, write the equation modeled by the envelopes and counters. Then solve it. 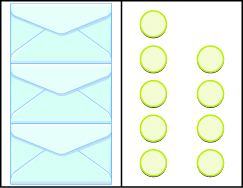This image has two columns. In the first column there are three envelopes. In the second column there are two vertical rows. The first row includes five blue circles, the second row includes four blue circles. 3x = 9; x = 3> This figure has two columns. In the first column there are two envelopes. In the second column there are two vertical rows, each includes four blue circles. Solve Equations Using the Division Property of Equality In the following exercises, solve each equation using the division property of equality and check the solution. [latex-display]8p=72[/latex-display] 9 [latex-display]-12q=48[/latex-display] [latex-display]-16r=-64[/latex-display] 4 [latex-display]-5s=-100[/latex-display] Translate to an Equation and Solve. In the following exercises, translate and solve. [latex-display]\text{The product of -6 and}y\text{is}-42[/latex-display] −6y = −42; y = 7 [latex-display]\text{The difference of}z\text{and -13 is -18.}[/latex-display] Four more than [latex]m[/latex] is [latex]-48[/latex]. m + 4 = −48; m = −52 [latex-display]\text{The product of -21 and}n\text{is 63.}[/latex-display]

Everyday Math

Describe how you have used two topics from this chapter in your life outside of your math class during the past month.

Chapter Practice Test

Locate and label [latex]0,2,-4[/latex], and [latex]-1[/latex] on a number line. In the following exercises, compare the numbers, using [latex]<\text{or}>\text{or}\text{=.}[/latex]
  1. ⓐ [latex]-6\text{__}3[/latex]
  2. ⓑ [latex]-1\text{__}-4[/latex]
  1. ⓐ <
  2. ⓑ >
  1. ⓐ [latex]-5\text{__}|-5|[/latex]
  2. ⓑ [latex]-|-2|\text{__}-2[/latex]
In the following exercises, find the opposite of each number.
  1. ⓐ [latex]-7[/latex]
  2. ⓑ [latex]8[/latex]
  1. ⓐ 7
  2. ⓑ −8
In the following exercises, simplify. [latex-display]-\left(-22\right)[/latex-display] [latex-display]|4 - 9|[/latex-display] 5 [latex-display]-8+6[/latex-display] [latex-display]-15+\left(-12\right)[/latex-display] −27 [latex-display]-7-\left(-3\right)[/latex-display] [latex-display]10-\left(5 - 6\right)[/latex-display] 11 [latex-display]-3\cdot 8[/latex-display] [latex-display]-6\left(-9\right)[/latex-display] 54 [latex-display]70\div \left(-7\right)[/latex-display] [latex-display]{\left(-2\right)}^{3}[/latex-display] −8 [latex-display]-{4}^{2}[/latex-display] [latex-display]16 - 3\left(5 - 7\right)[/latex-display] 22 [latex-display]|21 - 6|-|-8|[/latex-display] In the following exercises, evaluate. [latex-display]35-a\text{when}a=-4[/latex-display] 39 [latex-display]{\left(-2r\right)}^{2}\text{when}r=3[/latex-display] [latex-display]3m - 2n\text{when}m=6,n=-8[/latex-display] 34 [latex-display]-|-y|\text{when}y=17[/latex-display] In the following exercises, translate each phrase into an algebraic expression and then simplify, if possible. the difference of −7 and −4 −7 − (−4) = −3 the quotient of [latex]25[/latex] and the sum of [latex]m[/latex] and [latex]n[/latex]. In the following exercises, solve. Early one morning, the temperature in Syracuse was [latex]-8\text{^\circ F.}[/latex] By noon, it had risen [latex]\text{12^\circ .}[/latex] What was the temperature at noon? 4°F Collette owed [latex]\text{$128}[/latex] on her credit card. Then she charged [latex]\text{$65.}[/latex] What was her new balance? In the following exercises, solve. [latex-display]n+6=5[/latex-display] n = −1 [latex-display]p - 11=-4[/latex-display] [latex-display]-9r=-54[/latex-display] r = 6 In the following exercises, translate and solve. [latex-display]\text{The product of 15 and}x\text{is 75.}[/latex-display] [latex-display]\text{Eight less than}y\text{is -32.}[/latex-display] y − 8 = −32; y = −24  

Licenses & Attributions

CC licensed content, Specific attribution