Exponential Notation
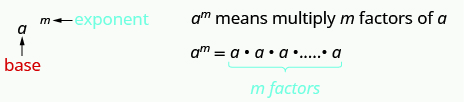
This is read [latex]a[/latex] to the [latex]{m}^{\mathrm{th}}[/latex] power.
In the expression [latex]{a}^{m}[/latex], the exponent tells us how many times we use the base [latex]a[/latex] as a factor.
example
Simplify:
1. [latex]{5}^{3}[/latex]
2. [latex]{9}^{1}[/latex]
Solution
| 1. |
|
|
[latex]{5}^{3}[/latex] |
| Multiply [latex]3[/latex] factors of [latex]5[/latex]. |
[latex]5\cdot 5\cdot 5[/latex] |
| Simplify. |
[latex]125[/latex] |
| 2. |
|
|
[latex]{9}^{1}[/latex] |
| Multiply [latex]1[/latex] factor of [latex]9[/latex]. |
[latex]9[/latex] |
example
Simplify:
1. [latex]{\left(\frac{7}{8}\right)}^{2}[/latex]
2. [latex]{\left(0.74\right)}^{2}[/latex]
Answer:
Solution
| 1. |
|
|
[latex]{\left(\frac{7}{8}\right)}^{2}[/latex] |
| Multiply two factors. |
[latex]\left(\frac{7}{8}\right)\left(\frac{7}{8}\right)[/latex] |
| Simplify. |
[latex]\frac{49}{64}[/latex] |
| 2. |
|
|
[latex]{\left(0.74\right)}^{2}[/latex] |
| Multiply two factors. |
[latex]\left(0.74\right)\left(0.74\right)[/latex] |
| Simplify. |
[latex]0.5476[/latex] |
example
Simplify:
1. [latex]{\left(-3\right)}^{4}[/latex]
2. [latex]{-3}^{4}[/latex]
Answer:
Solution
| 1. |
|
|
[latex]{\left(-3\right)}^{4}[/latex] |
| Multiply four factors of [latex]−3[/latex]. |
[latex]\left(-3\right)\left(-3\right)\left(-3\right)\left(-3\right)[/latex] |
| Simplify. |
[latex]81[/latex] |
| 2. |
|
|
[latex]{-3}^{4}[/latex] |
| Multiply two factors. |
[latex]-\left(3\cdot 3\cdot 3\cdot 3\right)[/latex] |
| Simplify. |
[latex]-81[/latex] |
Notice the similarities and differences in parts 1 and 2. Why are the answers different? In part 1 the parentheses tell us to raise the [latex](−3)[/latex] to the [latex]4[/latex]
th power. In part 2 we raise only the [latex]3[/latex] to the [latex]4[/latex]
th power and then find the opposite.
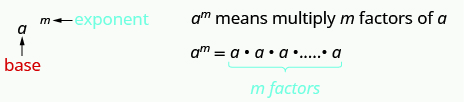 This is read [latex]a[/latex] to the [latex]{m}^{\mathrm{th}}[/latex] power.
This is read [latex]a[/latex] to the [latex]{m}^{\mathrm{th}}[/latex] power.
 Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
