We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Prealgebra

Using the Properties of Circles to Solve Problems

Learning Outcomes

  • Find the circumference and area of a circular object given it's radius
  • Find the circumference and area of a circular object given it's diameter
  • Calculate the diameter of a circular object given it's circumference
 

Do you remember the properties of circles from Decimals and Fractions Together? We’ll show them here again to refer to as we use them to solve applications.

Properties of Circles

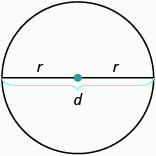
An image of a circle is shown. There is a line drawn through the widest part at the center of the circle with a red dot indicating the center of the circle. The line is labeled d. The two segments from the center of the circle to the outside of the circle are each labeled r.
  • [latex]r[/latex] is the length of the radius
  • [latex]d[/latex] is the length of the diameter
  • [latex]d=2r[/latex]
  • Circumference is the perimeter of a circle. The formula for circumference is[latex]C=2\pi r[/latex]
  • The formula for area of a circle is[latex]A=\pi {r}^{2}[/latex]
  Remember, that we approximate [latex]\pi [/latex] with [latex]3.14[/latex] or [latex]\frac{22}{7}[/latex] depending on whether the radius of the circle is given as a decimal or a fraction. If you use the [latex]\pi [/latex] key on your calculator to do the calculations in this section, your answers will be slightly different from the answers shown. That is because the [latex]\pi [/latex] key uses more than two decimal places.

example

A circular sandbox has a radius of [latex]2.5[/latex] feet. Find the 1. circumference and 2. area of the sandbox. Solution
1. Step 1. Read the problem. Draw the figure and label it with the given information. .
Step 2. Identify what you are looking for. the circumference of the circle
Step 3. Name. Choose a variable to represent it. Let c = circumference of the circle
Step 4. Translate. Write the appropriate formula Substitute [latex]C=2\pi r[/latex] [latex]C=2\pi \left(2.5\right)[/latex]
Step 5. Solve the equation. [latex]C\approx 2\left(3.14\right)\left(2.5\right)[/latex] [latex]C\approx 15\text{ft}[/latex]
Step 6. Check. Does this answer make sense? Yes. If we draw a square around the circle, its sides would be [latex]5[/latex] ft (twice the radius), so its perimeter would be [latex]20[/latex] ft. This is slightly more than the circle's circumference, [latex]15.7[/latex] ft. .
Step 7. Answer the question. The circumference of the sandbox is [latex]15.7[/latex] feet.
2. Step 1. Read the problem. Draw the figure and label it with the given information. .
Step 2. Identify what you are looking for. the area of the circle
Step 3. Name. Choose a variable to represent it. Let A = the area of the circle
Step 4. Translate. Write the appropriate formula Substitute [latex]A=\pi {r}^{2}[/latex] [latex]A=\pi{\left(2.5\right)}^{2}[/latex]
Step 5. Solve the equation. [latex]A\approx \left(3.14\right){\left(2.5\right)}^{2}[/latex] [latex]A\approx 19.625\text{sq. ft}[/latex]
Step 6. Check. Yes. If we draw a square around the circle, its sides would be [latex]5[/latex] ft, as shown in part ⓐ. So the area of the square would be [latex]25[/latex] sq. ft. This is slightly more than the circle's area, [latex]19.625[/latex] sq. ft.
Step 7. Answer the question. The area of the circle is [latex]19.625[/latex] square feet.
 

try it

[ohm_question]146563[/ohm_question] [ohm_question]146564[/ohm_question]
  We usually see the formula for circumference in terms of the radius [latex]r[/latex] of the circle: [latex-display]C=2\pi r[/latex-display] But since the diameter of a circle is two times the radius, we could write the formula for the circumference in terms [latex]\text{of}d[/latex]. [latex-display]\begin{array}{cccc}& & & C=2\pi r\hfill \\ \text{Using the commutative property, we get}\hfill & & & C=\pi \cdot 2r\hfill \\ \text{Then substituting}d=2r\hfill & & & C=\pi \cdot d\hfill \\ \text{So}\hfill & & & C=\pi d\hfill \end{array}[/latex-display] We will use this form of the circumference when we’re given the length of the diameter instead of the radius.  

example

A circular table has a diameter of four feet. What is the circumference of the table?

Answer: Solution

Step 1. Read the problem. Draw the figure and label it with the given information. .
Step 2. Identify what you are looking for. the circumference of the table
Step 3. Name. Choose a variable to represent it. Let c = the circumference of the table
Step 4. Translate. Write the appropriate formula for the situation. Substitute. [latex]C=\pi d[/latex] [latex]C=\pi \left(4\right)[/latex]
Step 5. Solve the equation, using [latex]3.14[/latex] for [latex]\pi [/latex]. [latex]C\approx \left(3.14\right)\left(4\right)[/latex] [latex]C\approx 12.56\text{feet}[/latex]
Step 6. Check: If we put a square around the circle, its side would be [latex]4[/latex]. The perimeter would be [latex]16[/latex]. It makes sense that the circumference of the circle, [latex]12.56[/latex], is a little less than [latex]16[/latex]. .
Step 7. Answer the question. The diameter of the table is [latex]12.56[/latex] square feet.

 

try it

[ohm_question]146785[/ohm_question] [ohm_question]146786[/ohm_question]
 

example

Find the diameter of a circle with a circumference of [latex]47.1[/latex] centimeters.

Answer: Solution

Step 1. Read the problem. Draw the figure and label it with the given information. . [latex]C=47.1[/latex]cm
Step 2. Identify what you are looking for. the diameter of the circle
Step 3. Name. Choose a variable to represent it. Let [latex]d[/latex] = the diameter of the circle
Step 4. Translate.
Write the formula. Substitute, using [latex]3.14[/latex] to approximate [latex]\pi [/latex] . [latex]C=\pi{d}[/latex] [latex]47.1\approx{3.14d}[/latex]
Step 5. Solve. [latex]\frac{47.1}{3.14}\approx\frac{3.14d}{3.14}[/latex] [latex]15\approx{d}[/latex]
Step 6. Check: [latex]C=\pi{d}[/latex] [latex-display]47.1\stackrel{?}{=}\left(3.14\right)\left(15\right)[/latex-display] [latex]47.1=47.1\quad\checkmark [/latex]
Step 7. Answer the question. The diameter of the circle is approximately [latex]15[/latex] centimeters.

 

try it

[ohm_question]146787[/ohm_question]
 

Licenses & Attributions

CC licensed content, Original

  • Question ID 146787, 146786, 146785. Authored by: Lumen Learning. License: CC BY: Attribution.

CC licensed content, Specific attribution