We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

מדריכי לימוד > Prealgebra

Using the Properties of Triangles to Solve Problems

Learning Outcomes

  • Given the measures of two angles of a triangle, find the third
  • Use properties of similar triangles to find unknown lengths of triangles
 

Using the Properties of Triangles to Solve Problems

What do you already know about triangles? Triangle have three sides and three angles. Triangles are named by their vertices. The triangle below is called [latex]\Delta ABC[/latex], read ‘triangle [latex]\text{ABC}[/latex] ’. We label each side with a lower case letter to match the upper case letter of the opposite vertex.

[latex-display]\Delta ABC[/latex] has vertices [latex]A,B,\text{ and }C[/latex] and sides [latex]a,b,\text{ and }c\text{.}[/latex-display]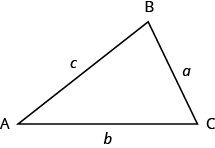 The vertices of the triangle on the left are labeled A, B, and C. The sides are labeled a, b, and c. The three angles of a triangle are related in a special way. The sum of their measures is [latex]\text{180}^ \circ[/latex]. [latex-display]m\angle A+m\angle B+m\angle C=\text{180}^ \circ[/latex-display]

Sum of the Measures of the Angles of a Triangle

For any [latex]\Delta ABC[/latex], the sum of the measures of the angles is [latex]\text{180}^ \circ[/latex]. [latex-display]m\angle A+m\angle B+m\angle C=\text{180}^ \circ[/latex-display]
 

example

The measures of two angles of a triangle are [latex]55^\circ [/latex] and [latex]82^\circ [/latex]. Find the measure of the third angle. Solution
Step 1. Read the problem. Draw the figure and label it with the given information. .
Step 2. Identify what you are looking for. The measure of the third angle in the triangle.
Step 3. Name. Choose a variable to represent it. Let [latex]x=[/latex]the measure of the angle.
Step 4. Translate. Write the appropriate formula and substitute. [latex]m\angle A+m\angle B+m\angle C=180[/latex]
Step 5. Solve the equation. [latex]55+82+x=180[/latex] [latex-display]137+x=180[/latex-display] [latex]x=43[/latex]
Step 6. Check: [latex-display]55+82+43\stackrel{?}{=}180[/latex-display] [latex]180=180\checkmark[/latex]
Step 7. Answer the question. The measure of the third angle is [latex]43°[/latex]
 

try it

[ohm_question]146498[/ohm_question]
 

Right Triangles

Some triangles have special names. We will look first at the right triangle. A right triangle has one [latex]\text{90^\circ }[/latex] angle, which is often marked with the symbol shown in the triangle below.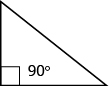 A right triangle is shown. The right angle is marked with a box and labeled 90 degrees. If we know that a triangle is a right triangle, we know that one angle measures [latex]\text{90^\circ }[/latex] so we only need the measure of one of the other angles in order to determine the measure of the third angle.

example

One angle of a right triangle measures [latex]28^\circ [/latex]. What is the measure of the third angle?

Answer: Solution

Step 1. Read the problem. Draw the figure and label it with the given information. .
Step 2. Identify what you are looking for. The measure of an angle.
Step 3. Name. Choose a variable to represent it. Let [latex]x=[/latex]the measure of the angle.
Step 4. Translate. Write the appropriate formula and substitute. [latex]m\angle A+m\angle B+m\angle C=180[/latex]
Step 5. Solve the equation. [latex]x+90+28=180[/latex] [latex-display]x+118=180[/latex-display] [latex]x=62[/latex]
Step 6. Check: [latex-display]180\stackrel{?}{=}90+28+62[/latex-display] [latex]180=180\checkmark[/latex]
Step 7. Answer the question. The measure of the third angle is [latex]62°[/latex]

 

try it

[ohm_question]146499[/ohm_question]
  In the examples so far, we could draw a figure and label it directly after reading the problem. In the next example, we will have to define one angle in terms of another. So we will wait to draw the figure until we write expressions for all the angles we are looking for.

example

The measure of one angle of a right triangle is [latex]20^\circ [/latex] more than the measure of the smallest angle. Find the measures of all three angles.

Answer: Solution

Step 1. Read the problem.
Step 2. Identify what you are looking for. the measures of all three angles
Step 3. Name. Choose a variable to represent it. Now draw the figure and label it with the given information. Let [latex]a={1}^{st}[/latex] angle. [latex]a+20={2}^{nd}[/latex] angle. [latex]90={3}^{rd}[/latex] angle (the right angle). .
Step 4. Translate. Write the appropriate formula and substitute into the formula. [latex]m\angle A+m\angle B+m\angle C=180[/latex] [latex]a+(a+20)+90=180[/latex]
Step 5. Solve the equation. [latex]2a+110=180[/latex] [latex-display]2a=70[/latex-display] [latex]a=35[/latex] first angle [latex]a+20[/latex] second angle [latex-display]\color{red}{35}+20[/latex-display] [latex-display]55[/latex-display] [latex]90[/latex] third angle.
Step 6. Check: [latex-display]35+55+90\stackrel{?}{=}180[/latex-display] [latex]180=180\checkmark[/latex]
Step 7. Answer the question. The three angles measure [latex]35°, 55°, 90°[/latex]

 

try it

[ohm_question]146500[/ohm_question]
 

Similar Triangles

When we use a map to plan a trip, a sketch to build a bookcase, or a pattern to sew a dress, we are working with similar figures. In geometry, if two figures have exactly the same shape but different sizes, we say they are similar figures. One is a scale model of the other. The corresponding sides of the two figures have the same ratio, and all their corresponding angles are have the same measures. The two triangles below are similar. Each side of [latex]\Delta ABC[/latex] is four times the length of the corresponding side of [latex]\Delta XYZ[/latex] and their corresponding angles have equal measures. [latex]\Delta ABC[/latex] and [latex]\Delta XYZ[/latex] are similar triangles. Their corresponding sides have the same ratio and the corresponding angles have the same measure.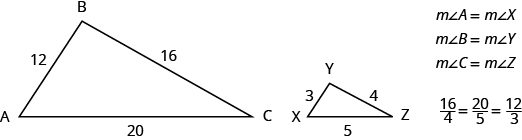 Two triangles are shown. They appear to be the same shape, but the triangle on the right is smaller. The vertices of the triangle on the left are labeled A, B, and C. The side across from A is labeled 16, the side across from B is labeled 20, and the side across from C is labeled 12. The vertices of the triangle on the right are labeled X, Y, and Z. The side across from X is labeled 4, the side across from Y is labeled 5, and the side across from Z is labeled 3. Beside the triangles, it says that the measure of angle A equals the measure of angle X, the measure of angle B equals the measure of angle Y, and the measure of angle C equals the measure of angle Z. Below this is the proportion 16 over 4 equals 20 over 5 equals 12 over 3.

Properties of Similar Triangles

If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths are in the same ratio. ...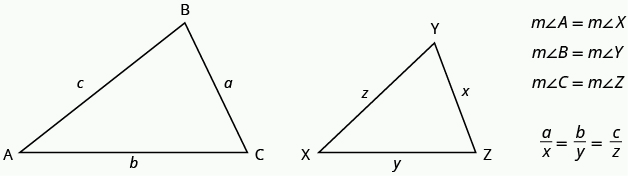
  The length of a side of a triangle may be referred to by its endpoints, two vertices of the triangle. For example, in [latex]\Delta ABC\text{:}[/latex] [latex-display]\begin{array}{c}\text{the length}a\text{can also be written}BC\hfill \\ \text{the length}b\text{can also be written}AC\hfill \\ \text{the length}c\text{can also be written}AB\hfill \end{array}[/latex-display] We will often use this notation when we solve similar triangles because it will help us match up the corresponding side lengths.  

example

[latex]\Delta ABC[/latex] and [latex]\Delta XYZ[/latex] are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.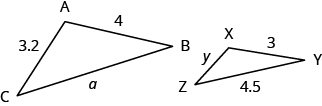 Two triangles are shown. They appear to be the same shape, but the triangle on the right is smaller. The vertices of the triangle on the left are labeled A, B, and C. The side across from A is labeled a, the side across from B is labeled 3.2, and the side across from C is labeled 4. The vertices of the triangle on the right are labeled X, Y, and Z. The side across from X is labeled 4.5, the side across from Y is labeled y, and the side across from Z is labeled 3.

Answer: Solution

Step 1. Read the problem. Draw the figure and label it with the given information. The figure is provided.
Step 2. Identify what you are looking for. The length of the sides of similar triangles
Step 3. Name. Choose a variable to represent it. Let a = length of the third side of [latex]\Delta ABC[/latex] y = length of the third side [latex]\Delta XYZ[/latex]
Step 4. Translate.
The triangles are similar, so the corresponding sides are in the same ratio. So [latex-display]\frac{AB}{XY}=\frac{BC}{YZ}=\frac{AC}{XZ}[/latex-display] Since the side [latex]AB=4[/latex] corresponds to the side [latex]XY=3[/latex] , we will use the ratio [latex]\frac{\mathrm{AB}}{\mathrm{XY}}=\frac{4}{3}[/latex] to find the other sides. Be careful to match up corresponding sides correctly. .
Step 5. Solve the equation. .
Step 6. Check: .
Step 7. Answer the question. The third side of [latex]\Delta ABC[/latex] is [latex]6[/latex] and the third side of [latex]\Delta XYZ[/latex] is [latex]2.4[/latex].

 

try it

[ohm_question]146912[/ohm_question]
 

Licenses & Attributions

CC licensed content, Original

  • Question ID 146912, 146498, 146499, 146500. Authored by: Lumen Learning. License: CC BY: Attribution.

CC licensed content, Specific attribution