Solutions 15: Graphs of Polynomial Functions
Solutions to Try Its
1. y-intercept [latex]\left(0,0\right)[/latex]; x-intercepts [latex]\left(0,0\right),\left(-5,0\right),\left(2,0\right)[/latex], and [latex]\left(3,0\right)[/latex] 2. The graph has a zero of –5 with multiplicity 1, a zero of –1 with multiplicity 2, and a zero of 3 with even multiplicity. 3.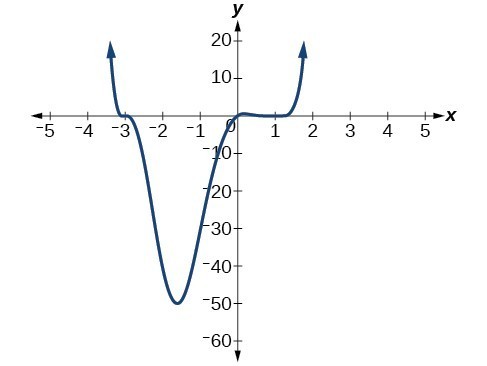
4. Because f is a polynomial function and since [latex]f\left(1\right)[/latex] is negative and [latex]f\left(2\right)[/latex] is positive, there is at least one real zero between [latex]x=1[/latex] and [latex]x=2[/latex].
5. [latex]f\left(x\right)=-\frac{1}{8}{\left(x - 2\right)}^{3}{\left(x+1\right)}^{2}\left(x - 4\right)[/latex]
6. The minimum occurs at approximately the point [latex]\left(0,-6.5\right)[/latex], and the maximum occurs at approximately the point [latex]\left(3.5,7\right)[/latex].
Solutions to Odd-Numbered Exercises
1. The x-intercept is where the graph of the function crosses the x-axis, and the zero of the function is the input value for which [latex]f\left(x\right)=0[/latex]. 3. If we evaluate the function at a and at b and the sign of the function value changes, then we know a zero exists between a and b. 5. There will be a factor raised to an even power. 7. [latex]\left(-2,0\right),\left(3,0\right),\left(-5,0\right)[/latex] 9. [latex]\left(3,0\right),\left(-1,0\right),\left(0,0\right)[/latex] 11. [latex]\left(0,0\right),\text{ }\left(-5,0\right),\text{ }\left(2,0\right)[/latex] 13. [latex]\left(0,0\right),\text{ }\left(-5,0\right),\text{ }\left(4,0\right)[/latex] 15. [latex]\left(2,0\right),\text{ }\left(-2,0\right),\text{ }\left(-1,0\right)[/latex] 17. [latex]\left(-2,0\right),\left(2,0\right),\left(\frac{1}{2},0\right)[/latex] 19. [latex]\left(1,0\right),\text{ }\left(-1,0\right)[/latex] 21. [latex]\left(0,0\right),\left(\sqrt{3},0\right),\left(-\sqrt{3},0\right)[/latex] 23. [latex]\left(0,0\right),\text{ }\left(1,0\right)\text{, }\left(-1,0\right),\text{ }\left(2,0\right),\text{ }\left(-2,0\right)[/latex] 25. [latex]f\left(2\right)=-10[/latex] and [latex]f\left(4\right)=28[/latex]. Sign change confirms. 27. [latex]f\left(1\right)=3[/latex] and [latex]f\left(3\right)=-77[/latex]. Sign change confirms. 29. [latex]f\left(0.01\right)=1.000001[/latex] and [latex]f\left(0.1\right)=-7.999[/latex]. Sign change confirms. 31. 0 with multiplicity 2, [latex]-\frac{3}{2}[/latex] with multiplicity 5, 4 with multiplicity 2 33. 0 with multiplicity 2, –2 with multiplicity 2 35. [latex]-\frac{2}{3}\text{ with multiplicity }5\text{,}5\text{ with multiplicity }\text{2}[/latex] 37. [latex]\text{0}\text{ with multiplicity }4\text{,}2\text{ with multiplicity }1\text{,}-\text{1}\text{ with multiplicity }1[/latex] 39. [latex]\frac{3}{2}[/latex] with multiplicity 2, 0 with multiplicity 3 41. [latex]\text{0}\text{ with multiplicity }6\text{,}\frac{2}{3}\text{ with multiplicity }2[/latex] 43. x-intercepts, [latex]\left(1, 0\right)[/latex] with multiplicity 2, [latex]\left(-4, 0\right)[/latex] with multiplicity 1, y-intercept [latex]\left(0, 4\right)[/latex]. As [latex]x\to -\infty [/latex] , [latex]f\left(x\right)\to -\infty [/latex] , as [latex]x\to \infty [/latex] , [latex]f\left(x\right)\to \infty [/latex] .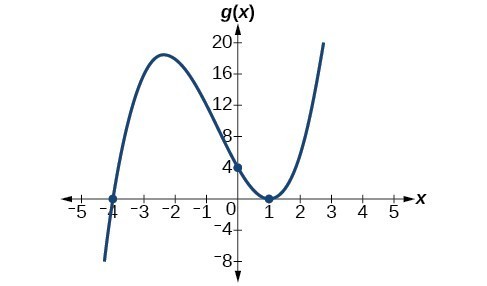
45. x-intercepts [latex]\left(3,0\right)[/latex] with multiplicity 3, [latex]\left(2,0\right)[/latex] with multiplicity 2, y-intercept [latex]\left(0,-108\right)[/latex] . As [latex]x\to -\infty [/latex], [latex]f\left(x\right)\to -\infty [/latex] , as [latex]x\to \infty [/latex] , [latex]f\left(x\right)\to \infty [/latex].
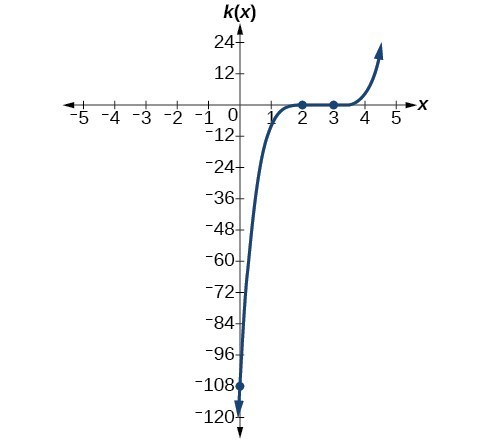47. x-intercepts [latex]\left(0, 0\right),\left(-2, 0\right),\left(4, 0\right)[/latex] with multiplicity 1, y-intercept [latex]\left(0, 0\right)[/latex]. As [latex]x\to -\infty [/latex] , [latex]f\left(x\right)\to \infty [/latex] , as [latex]x\to \infty [/latex] , [latex]f\left(x\right)\to -\infty [/latex].
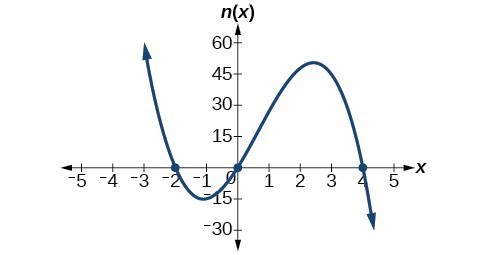49. [latex]f\left(x\right)=-\frac{2}{9}\left(x - 3\right)\left(x+1\right)\left(x+3\right)[/latex]
51. [latex]f\left(x\right)=\frac{1}{4}{\left(x+2\right)}^{2}\left(x - 3\right)[/latex]
53. –4, –2, 1, 3 with multiplicity 1
55. –2, 3 each with multiplicity 2
57. [latex]f\left(x\right)=-\frac{2}{3}\left(x+2\right)\left(x - 1\right)\left(x - 3\right)[/latex]
59. [latex]f\left(x\right)=\frac{1}{3}{\left(x - 3\right)}^{2}{\left(x - 1\right)}^{2}\left(x+3\right)[/latex]
61. [latex]f\left(x\right)=-15{\left(x - 1\right)}^{2}{\left(x - 3\right)}^{3}[/latex]
63. [latex]f\left(x\right)=-2\left(x+3\right)\left(x+2\right)\left(x - 1\right)[/latex]
65. [latex]f\left(x\right)=-\frac{3}{2}{\left(2x - 1\right)}^{2}\left(x - 6\right)\left(x+2\right)[/latex]
67. local max [latex]\left(-\text{.58, -}.62\right)[/latex], local min [latex]\left(\text{.58, -1}\text{.38}\right)[/latex]
69. global min [latex]\left(-\text{.63, -}\text{.47}\right)[/latex]
71. global min [latex]\text{(}\text{.75, }\text{.89)}[/latex]
73. [latex]f\left(x\right)={\left(x - 500\right)}^{2}\left(x+200\right)[/latex]
75. [latex]f\left(x\right)=4{x}^{3}-36{x}^{2}+80x[/latex]
77. [latex]f\left(x\right)=4{x}^{3}-36{x}^{2}+60x+100[/latex]
79. [latex]f\left(x\right)=\pi \left(9{x}^{3}+45{x}^{2}+72x+36\right)[/latex]Licenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
