Solutions for Modeling with Trigonometric Equations
Solutions to Try Its
1. The amplitude is , and the period is . 2.| x | |
|---|---|
| 0 | 0 |
| 3 | |
| 0 | |
| 0 |
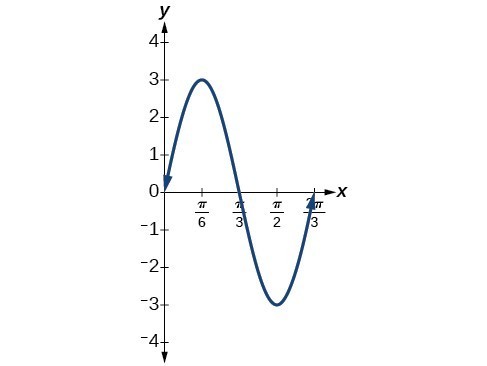 3.
The temperature reaches freezing at noon and at midnight.
3.
The temperature reaches freezing at noon and at midnight.
 4. initial displacement =6, damping constant = -6, frequency =
5.
6.
4. initial displacement =6, damping constant = -6, frequency =
5.
6.
Solutions to Odd-Numbered Exercises
1. Physical behavior should be periodic, or cyclical. 3. Since cumulative rainfall is always increasing, a sinusoidal function would not be ideal here. 5. 7. 9. 11. 13. 15. Answers will vary. Sample answer: This function could model temperature changes over the course of one very hot day in Phoenix, Arizona.![Graph of f(x) = -18cos(x*pi/12) - 5sin(x*pi/12) + 100 on the interval [0,24]. There is a single peak around 12.](https://s3-us-west-2.amazonaws.com/courses-images-archive-read-only/wp-content/uploads/sites/923/2015/04/25001621/CNX_Precalc_Figure_07_06_202.jpg) 17. 9 years from now
19.
21. hours
23. 4:30
25. From July 8 to October 23
27. From day 19 through day 40
29. Floods: July 24 through October 7. Droughts: February 4 through March 27
31. Amplitude: 11, period: , frequency: 6 Hz
33. Amplitude: 5, period: , frequency: 30 Hz
35.
37.
39.
41.
43. years
45. 17.8 seconds
47. Spring 2 comes to rest first after 8.0 seconds.
49. 500 miles, at
51.
53.
17. 9 years from now
19.
21. hours
23. 4:30
25. From July 8 to October 23
27. From day 19 through day 40
29. Floods: July 24 through October 7. Droughts: February 4 through March 27
31. Amplitude: 11, period: , frequency: 6 Hz
33. Amplitude: 5, period: , frequency: 30 Hz
35.
37.
39.
41.
43. years
45. 17.8 seconds
47. Spring 2 comes to rest first after 8.0 seconds.
49. 500 miles, at
51.
53. 