We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Precalculus II

Solutions for Systems of Nonlinear Equations and Inequalities: Two Variables

Solutions to Try Its

1. [latex]\left(-\frac{1}{2},\frac{1}{2}\right)[/latex] and [latex]\left(2,8\right)[/latex] 2. [latex]\left(-1,3\right)[/latex] 3. [latex]\left\{\left(1,3\right),\left(1,-3\right),\left(-1,3\right),\left(-1,-3\right)\right\}[/latex] 4. Shade the area bounded by the two curves, above the quadratic and below the line. A line intersecting a parabola at the points negative one, zero and two, three. The region under the line but above the parabola is shaded.

Solutions to Odd-Numbered Exercises

1. A nonlinear system could be representative of two circles that overlap and intersect in two locations, hence two solutions. A nonlinear system could be representative of a parabola and a circle, where the vertex of the parabola meets the circle and the branches also intersect the circle, hence three solutions. 3. No. There does not need to be a feasible region. Consider a system that is bounded by two parallel lines. One inequality represents the region above the upper line; the other represents the region below the lower line. In this case, no points in the plane are located in both regions; hence there is no feasible region. 5. Choose any number between each solution and plug into [latex]C\left(x\right)[/latex] and [latex]R\left(x\right)[/latex]. If [latex]C\left(x\right)<R\left(x\right),\text{}[/latex] then there is profit. 7. [latex]\left(0,-3\right),\left(3,0\right)[/latex] 9. [latex]\left(-\frac{3\sqrt{2}}{2},\frac{3\sqrt{2}}{2}\right),\left(\frac{3\sqrt{2}}{2},-\frac{3\sqrt{2}}{2}\right)[/latex] 11. [latex]\left(-3,0\right),\left(3,0\right)[/latex] 13. [latex]\left(\frac{1}{4},-\frac{\sqrt{62}}{8}\right),\left(\frac{1}{4},\frac{\sqrt{62}}{8}\right)[/latex] 15. [latex]\left(-\frac{\sqrt{398}}{4},\frac{199}{4}\right),\left(\frac{\sqrt{398}}{4},\frac{199}{4}\right)[/latex] 17. [latex]\left(0,2\right),\left(1,3\right)[/latex] 19. [latex]\left(-\sqrt{\frac{1}{2}\left(\sqrt{5}-1\right)},\frac{1}{2}\left(1-\sqrt{5}\right)\right),\left(\sqrt{\frac{1}{2}\left(\sqrt{5}-1\right)},\frac{1}{2}\left(1-\sqrt{5}\right)\right)[/latex] 21. [latex]\left(5,0\right)[/latex] 23. [latex]\left(0,0\right)[/latex] 25. [latex]\left(3,0\right)[/latex] 27. No Solutions Exist 29. No Solutions Exist 31. [latex]\left(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right),\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right),\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right),\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)[/latex] 33. [latex]\left(2,0\right)[/latex] 35. [latex]\left(-\sqrt{7},-3\right),\left(-\sqrt{7},3\right),\left(\sqrt{7},-3\right),\left(\sqrt{7},3\right)[/latex] 37. [latex]\left(-\sqrt{\frac{1}{2}\left(\sqrt{73}-5\right)},\frac{1}{2}\left(7-\sqrt{73}\right)\right),\left(\sqrt{\frac{1}{2}\left(\sqrt{73}-5\right)},\frac{1}{2}\left(7-\sqrt{73}\right)\right)[/latex] 39. A dotted parabola. The region below the parabola is shaded. 41. A shaded figure with a dotted line that has two marked points. The first point is at square root of two minus 1, two times (the square root of two minus one). The second point is at negative one minus square root of two, negative two times (one plus the square root of two). 43. 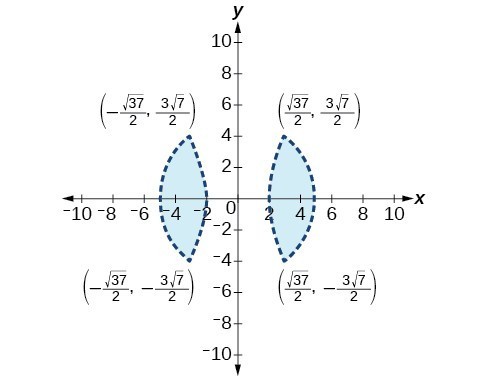Two dotted, shaded figures with points marked. The first point is (negative square root of 37 over 2, 3 times square root of seven over two). The second point is (square root of 37 over 2, 3 times square root of 7 over two). The third point is (negative square root 37 over 2, negative 3 times square root 7 divided by 2). The fourth point is (square root 37 over 2, negative 3 times square root of 7 over two). 45. 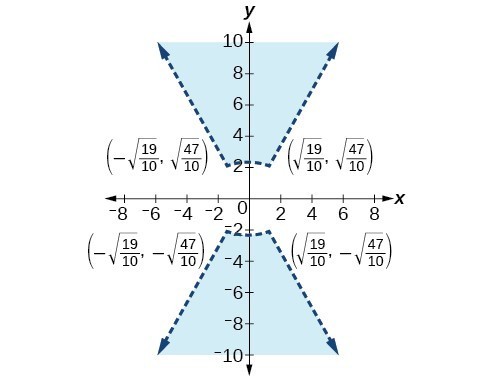Two dotted, shaded figures with marked points. The first point is negative square root of nineteen-tenths, square root of forty-seven-tenths. The second point is square root of 19 tenths, square root of 47 tenths. The third point is negative square root of 19 tenths, negative square root of 47 tenths. The fourth point is square root of 19 tenths, negative square root of 47 tenths. 47. Two solid curving lines. The region below the blue line and to the right of the y axis is shaded. 49. [latex]\left(-2\sqrt{\frac{70}{383}},-2\sqrt{\frac{35}{29}}\right),\left(-2\sqrt{\frac{70}{383}},2\sqrt{\frac{35}{29}}\right),\left(2\sqrt{\frac{70}{383}},-2\sqrt{\frac{35}{29}}\right),\left(2\sqrt{\frac{70}{383}},2\sqrt{\frac{35}{29}}\right)[/latex] 51. No Solution Exists 53. [latex]x=0,y>0[/latex] and [latex]0<x<1,\sqrt{x}<y<\frac{1}{x}[/latex] 55. 12, 288 57. 2–20 computers

Licenses & Attributions

CC licensed content, Specific attribution