We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > MATH 1314: College Algebra

Solutions

Solutions to Try Its

1. End behavior: as [latex]x\to \pm \infty , f\left(x\right)\to 0\\[/latex]; Local behavior: as [latex]x\to 0, f\left(x\right)\to \infty \\[/latex] (there are no x- or y-intercepts) 2. The function and the asymptotes are shifted 3 units right and 4 units down. As [latex]x\to 3,f\left(x\right)\to \infty\\ [/latex], and as [latex]x\to \pm \infty ,f\left(x\right)\to -4\\[/latex].

The function is [latex]f\left(x\right)=\frac{1}{{\left(x - 3\right)}^{2}}-4\\[/latex].

Graph of f(x)=1/(x-3)^2-4 with its vertical asymptote at x=3 and its horizontal asymptote at y=-4. 3. [latex]\frac{12}{11}\\[/latex] 4. The domain is all real numbers except [latex]x=1\\[/latex] and [latex]x=5\\[/latex]. 5. Removable discontinuity at [latex]x=5\\[/latex]. Vertical asymptotes: [latex]x=0,\text{ }x=1\\[/latex]. 6. Vertical asymptotes at [latex]x=2\\[/latex] and [latex]x=-3\\[/latex]; horizontal asymptote at [latex]y=4\\[/latex]. 7. For the transformed reciprocal squared function, we find the rational form. [latex]f\left(x\right)=\frac{1}{{\left(x - 3\right)}^{2}}-4=\frac{1 - 4{\left(x - 3\right)}^{2}}{{\left(x - 3\right)}^{2}}=\frac{1 - 4\left({x}^{2}-6x+9\right)}{\left(x - 3\right)\left(x - 3\right)}=\frac{-4{x}^{2}+24x - 35}{{x}^{2}-6x+9}\\[/latex]

Because the numerator is the same degree as the denominator we know that as [latex]x\to \pm \infty , f\left(x\right)\to -4; \text{so } y=-4\\[/latex] is the horizontal asymptote. Next, we set the denominator equal to zero, and find that the vertical asymptote is [latex]x=3\\[/latex], because as [latex]x\to 3,f\left(x\right)\to \infty \\[/latex]. We then set the numerator equal to 0 and find the x-intercepts are at [latex]\left(2.5,0\right)\\[/latex] and [latex]\left(3.5,0\right)\\[/latex]. Finally, we evaluate the function at 0 and find the y-intercept to be at [latex]\left(0,\frac{-35}{9}\right)\\[/latex].

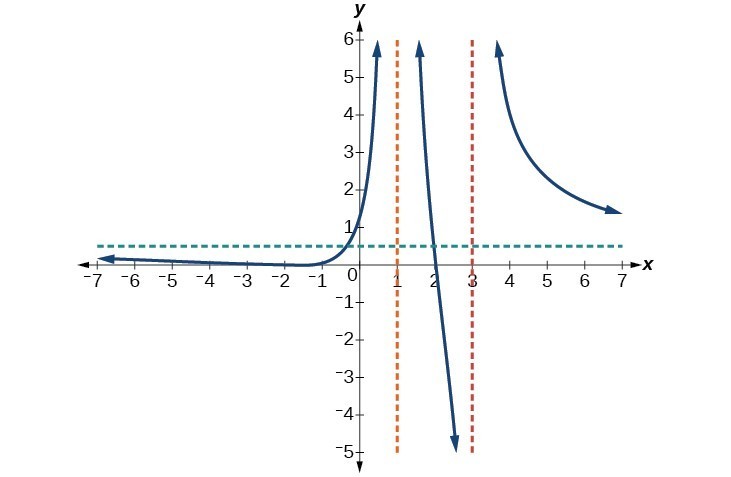
8. Horizontal asymptote at [latex]y=\frac{1}{2}\\[/latex]. Vertical asymptotes at [latex]x=1 \text{and} x=3\\[/latex]. y-intercept at [latex]\left(0,\frac{4}{3}.\right)\\[/latex]

x-intercepts at [latex]\left(2,0\right) \text{ and }\left(-2,0\right)\\[/latex]. [latex]\left(-2,0\right)\\[/latex] is a zero with multiplicity 2, and the graph bounces off the x-axis at this point. [latex]\left(2,0\right)\\[/latex] is a single zero and the graph crosses the axis at this point. Graph of f(x)=(x+2)^2(x-2)/2(x-1)^2(x-3) with its vertical and horizontal asymptotes.

Solutions to Try Its

1. The rational function will be represented by a quotient of polynomial functions. 3. The numerator and denominator must have a common factor. 5. Yes. The numerator of the formula of the functions would have only complex roots and/or factors common to both the numerator and denominator. 7. [latex]\text{All reals }x\ne -1, 1\\[/latex] 9. [latex]\text{All reals }x\ne -1, -2, 1, 2\\[/latex] 11. V.A. at [latex]x=-\frac{2}{5}\\[/latex]; H.A. at [latex]y=0\\[/latex]; Domain is all reals [latex]x\ne -\frac{2}{5}\\[/latex] 13. V.A. at [latex]x=4, -9\\[/latex]; H.A. at [latex]y=0\\[/latex]; Domain is all reals [latex]x\ne 4, -9\\[/latex] 15. V.A. at [latex]x=0, 4, -4\\[/latex]; H.A. at [latex]y=0\\[/latex]; Domain is all reals [latex]x\ne 0,4, -4\\[/latex] 17. V.A. at [latex]x=-5\\[/latex]; H.A. at [latex]y=0\\[/latex]; Domain is all reals [latex]x\ne 5,-5\\[/latex] 19. V.A. at [latex]x=\frac{1}{3}\\[/latex]; H.A. at [latex]y=-\frac{2}{3}\\[/latex]; Domain is all reals [latex]x\ne \frac{1}{3}\\[/latex]. 21. none 23. [latex]x\text{-intercepts none, }y\text{-intercept }\left(0,\frac{1}{4}\right)\\[/latex] 25. Local behavior: [latex]x\to -{\frac{1}{2}}^{+},f\left(x\right)\to -\infty ,x\to -{\frac{1}{2}}^{-},f\left(x\right)\to \infty \\[/latex] End behavior: [latex]x\to \pm \infty ,f\left(x\right)\to \frac{1}{2}\\[/latex] 27. Local behavior: [latex]x\to {6}^{+},f\left(x\right)\to -\infty ,x\to {6}^{-},f\left(x\right)\to \infty \\[/latex], End behavior: [latex]x\to \pm \infty ,f\left(x\right)\to -2\\[/latex] 29. Local behavior: [latex]x\to -{\frac{1}{3}}^{+},f\left(x\right)\to \infty ,x\to -{\frac{1}{3}}^{-}\\[/latex], [latex]f\left(x\right)\to -\infty ,x\to {\frac{5}{2}}^{-},f\left(x\right)\to \infty ,x\to {\frac{5}{2}}^{+}\\[/latex] , [latex]f\left(x\right)\to -\infty \\[/latex] End behavior: [latex]x\to \pm \infty\\ [/latex], [latex]f\left(x\right)\to \frac{1}{3}\\[/latex] 31. [latex]y=2x+4\\[/latex] 33. [latex]y=2x\\[/latex] 35. [latex]V.A.\text{ }x=0,H.A.\text{ }y=2\\[/latex] Graph of a rational function. 37. [latex]V.A.\text{ }x=2,\text{ }H.A.\text{ }y=0\\[/latex] Graph of a rational function. 39. [latex]V.A.\text{ }x=-4,\text{ }H.A.\text{ }y=2;\left(\frac{3}{2},0\right);\left(0,-\frac{3}{4}\right)\\[/latex] Graph of p(x)=(2x-3)/(x+4) with its vertical asymptote at x=-4 and horizontal asymptote at y=2. 41. [latex]V.A.\text{ }x=2,\text{ }H.A.\text{ }y=0,\text{ }\left(0,1\right)\\[/latex] Graph of s(x)=4/(x-2)^2 with its vertical asymptote at x=2 and horizontal asymptote at y=0. 43. [latex]V.A.\text{ }x=-4,\text{ }x=\frac{4}{3},\text{ }H.A.\text{ }y=1;\left(5,0\right);\left(-\frac{1}{3},0\right);\left(0,\frac{5}{16}\right)\\[/latex] 45. [latex]V.A.\text{ }x=-1,\text{ }H.A.\text{ }y=1;\left(-3,0\right);\left(0,3\right)\\[/latex] Graph of f(x)=(3x^2-14x-5)/(3x^2+8x-16) with its vertical asymptotes at x=-4 and x=4/3 and horizontal asymptote at y=1. 47. [latex]V.A.\text{ }x=4,\text{ }S.A.\text{ }y=2x+9;\left(-1,0\right);\left(\frac{1}{2},0\right);\left(0,\frac{1}{4}\right)\\[/latex] Graph of h(x)=(2x^2+x-1)/(x-1) with its vertical asymptote at x=4 and slant asymptote at y=2x+9. 49. [latex]V.A.\text{ }x=-2,\text{ }x=4,\text{ }H.A.\text{ }y=1,\left(1,0\right);\left(5,0\right);\left(-3,0\right);\left(0,-\frac{15}{16}\right)\\[/latex] Graph of w(x)=(x-1)(x+3)(x-5)/(x+2)^2(x-4) with its vertical asymptotes at x=-2 and x=4 and horizontal asymptote at y=1. 51. [latex]y=50\frac{{x}^{2}-x - 2}{{x}^{2}-25}\\[/latex] 53. [latex]y=7\frac{{x}^{2}+2x - 24}{{x}^{2}+9x+20}\\[/latex] 55. [latex]y=\frac{1}{2}\frac{{x}^{2}-4x+4}{x+1}\\[/latex] 57. [latex]y=4\frac{x - 3}{{x}^{2}-x - 12}\\[/latex] 59. [latex]y=-9\frac{x - 2}{{x}^{2}-9}\\[/latex] 61. [latex]y=\frac{1}{3}\frac{{x}^{2}+x - 6}{x - 1}\\[/latex] 63. [latex]y=-6\frac{{\left(x - 1\right)}^{2}}{\left(x+3\right){\left(x - 2\right)}^{2}}\\[/latex] 65.
x 2.01 2.001 2.0001 1.99 1.999
y 100 1,000 10,000 –100 –1,000
x 10 100 1,000 10,000 100,000
y .125 .0102 .001 .0001 .00001
Vertical asymptote [latex]x=2\\[/latex], Horizontal asymptote [latex]y=0\\[/latex] 67.
x –4.1 –4.01 –4.001 –3.99 –3.999
y 82 802 8,002 –798 –7998
x 10 100 1,000 10,000 100,000
y 1.4286 1.9331 1.992 1.9992 1.999992

Vertical asymptote [latex]x=-4\\[/latex], Horizontal asymptote [latex]y=2\\[/latex]

69.
x –.9 –.99 –.999 –1.1 –1.01
y 81 9,801 998,001 121 10,201
x 10 100 1,000 10,000 100,000
y .82645 .9803 .998 .9998
Vertical asymptote [latex]x=-1\\[/latex], Horizontal asymptote [latex]y=1\\[/latex] 71. [latex]\left(\frac{3}{2},\infty \right)\\[/latex] Graph of f(x)=4/(2x-3). 73. [latex]\left(-2,1\right)\cup \left(4,\infty \right)\\[/latex] Graph of f(x)=(x+2)/(x-1)(x-4). 75. [latex]\left(2,4\right)\\[/latex] 77. [latex]\left(2,5\right)\\[/latex] 79. [latex]\left(-1,\text{1}\right)\\[/latex] 81. [latex]C\left(t\right)=\frac{8+2t}{300+20t}\\[/latex] 83. After about 6.12 hours. 85. [latex]A\left(x\right)=50{x}^{2}+\frac{800}{x}\\[/latex]. 2 by 2 by 5 feet. 87. [latex]A\left(x\right)=\pi {x}^{2}+\frac{100}{x}\\[/latex]. Radius = 2.52 meters.

Licenses & Attributions

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..