We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Учебные пособия > Mathematics for the Liberal Arts

Surface Area

Learning Objectives

  • Understand nets.
  • Use nets to represent prisms.
  • Find the surface area of a prism.
  • Find the surface area of cylinders.
  • Find the surface area of a sphere.

Nets

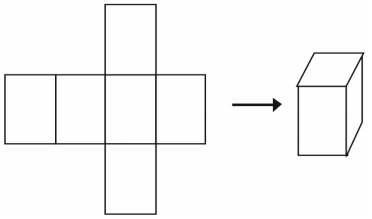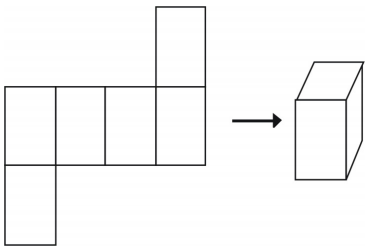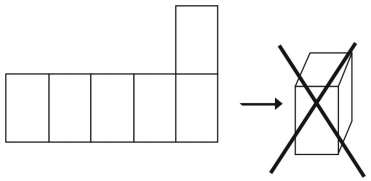
One final way to represent a solid is to use a net. If you cut out a net you can fold it into a model of a figure. Nets can also be used to analyze a single solid. Here is an example of a net for a cube. Fig2_1_1 There is more than one way to make a net for a single figure. Fig2_1_2 However, not all arrangements will create a cube. Fig2_1_3

Example 1

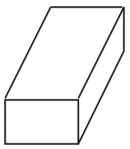
What kind of figure does the net create? Draw the figure.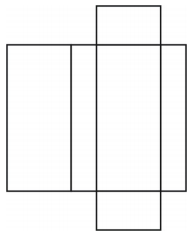 Fig2_1_4 The net creates a box-shaped rectangular prism as shown below. Fig2_1_5

Example 2

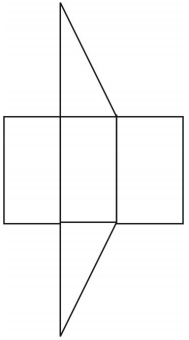
What kind of net can you draw to represent the figure shown? Draw the net.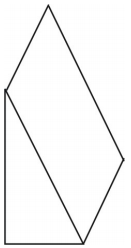 Fig2_1_6 A net for the prism is shown. Other nets are possible. Fig2_1_7

Review Exercises

Draw a net for each of the following:
  1. Fig2_1_8
  2. Fig2_1_9

Answers

  1. Fig2_1_10
  2. Fig2_1_11

Prisms

A prism is a three-dimensional figure with a pair of parallel and congruent ends, or bases. The sides of a prism are parallelograms. Prisms are identified by their bases.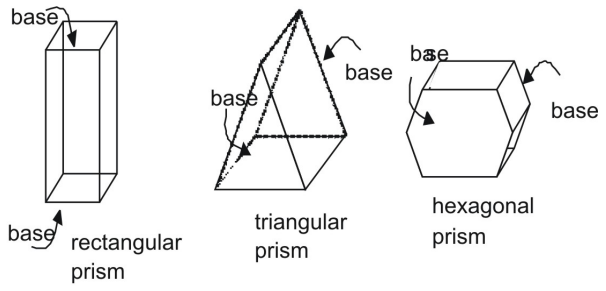 Fig2_1_12

Surface Area of a Prism Using Nets

The prisms above are right prisms. In a right prism, the lateral sides are perpendicular to the bases of prism. Compare a right prism to an oblique prism, in which sides and bases are not perpendicular.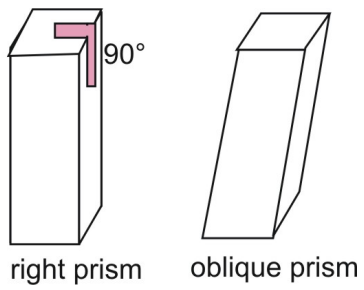 Fig2_1_13 Two postulates that apply to area are the Area Congruence Postulate and the Area Addition Postulate.
Area Congruence Postulate: If two polygons (or plane figures) are congruent, then their areas are congruent.
Area Addition Postulate: The surface area of a three-dimensional figure is the sum of the areas of all of its non-overlapping parts.
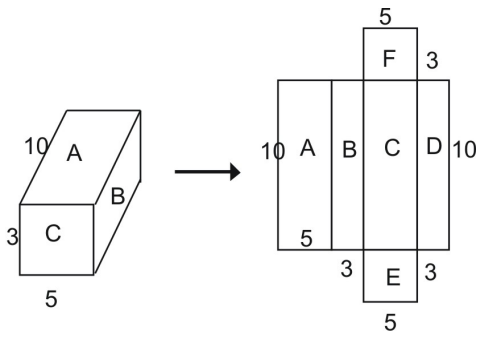You can use a net and the Area Addition Postulate to find the surface area of a right prism. Fig2_1_14 From the net, you can see that that the surface area of the entire prism equals the sum of the figures that make up the net: Total surface area = area A + area B + area C + area D + area E + area F Using the formula for the area of a rectangle, you can see that the area of rectangle A is:

A = l · w A = 10 · 5 = 50 square units

Similarly, the areas of the other rectangles are inserted back into the equation above.

Total surface area = area A + area B + area C + area D + area E + area F Total surface area = (10 · 5) + (10 · 3) + (10 · 5) + (10 · 3) + (5 · 3) + (5 · 3) Total surface area = 50 + 30 + 50 + 30 + 15 + 15 Total surface area =  190 square units

Example 3

Use a net to find the surface area of the prism.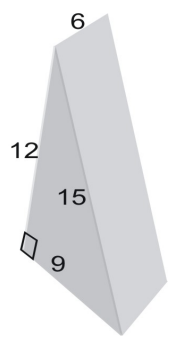 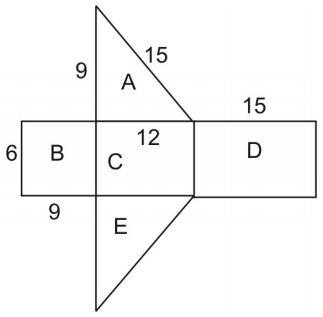Fig2_1_15Fig2_1_16 The area of the net is equal to the surface area of the figure. To find the area of the triangle, we use the formula:

[latex]\displaystyle{A}=\frac{1}{2}hb\\[/latex] where h is the height of the triangle and b is its base.

Note that triangles A and E are congruent so we can multiply the area of triangle A by 2.

[latex]\displaystyle\text{area}=\text{area }A+\text{area }B+\text{area }C+\text{area }D+\text{area }E\\[/latex] [latex-display]\displaystyle\text{ }=2(\text{area }A)+\text{area }B+\text{area }C+\text{area }D\\[/latex-display] [latex-display]\displaystyle\text{ }=2[\frac{1}{2}(9\cdot{12})]+(6\cdot9)+(6\cdot12)+(6\cdot12)\\[/latex-display] [latex]\displaystyle\text{ }=108+54+72+90=324\\[/latex]

Thus, the surface area is 324 square units.

Review Exercises

For each of the following find the surface are a using the method of nets and the perimeter
  1. Fig2_1_17
  2. Fig2_1_18
  3. The base of a prism is a right triangle whose legs are 3 and 4 and show height is 20. What is the total area of the prism?
  4. A right hexagonal prism is 24 inches tall and has bases that are regular hexagons measuring 8 inches on a side. What is the total surface area?
  5. What is the volume of the prism in problem #4?
In the following questions, a barn is shaped like a pentagonal prism with dimensions shown in feet: Fig2_1_19
  1. How many square feet (excluding the roof) are there on the surface of the barn to be painted?
  2. If a gallon of paint covers 250 square feet, how many gallons of paint are needed to paint the barn?
  3. A cardboard box is a perfect cube with an edge measuring 17 inches. How many cubic feet can it hold?
  4. A swimming pool is 16 feet wide, 32 feet long and is uniformly 4 feet deep. How many cubic feet of water can it hold?
  5. A cereal box has length 25 cm, width 9 cm and height 30 cm. How much cereal can it hold?

Answers

Nets and perimeter:
  1. 40.5 in2
  2. 838 cm2
  3. 252 square units
  4. 1484.6 square units
  5. 3990.7 cubic inches
The barn:
  1. 2450 square feet
  2. 10 gallons of paint
  3. 2.85 cubic feet (be careful here. The units in the problem are given in inches but the question asks for feet.)
  4. 2048 cubic feet
  5. 6750 cm3

Cylinders

A cylinder is a three-dimensional figure with a pair of parallel and congruent circular ends, or bases. A cylinder has a single curved side that forms a rectangle when laid out flat. As with prisms, cylinders can be right or oblique. The side of a right cylinder is perpendicular to its circular bases. The side of an oblique cylinder is not perpendicular to its bases.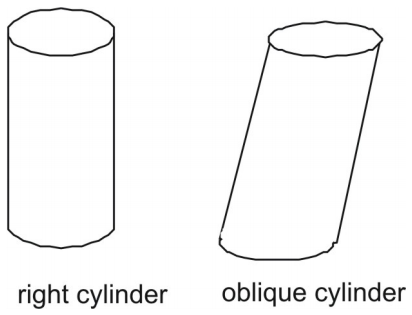 Fig2_1_20

Surface Area of a Cylinder Using Nets

You can deconstruct a cylinder into a net.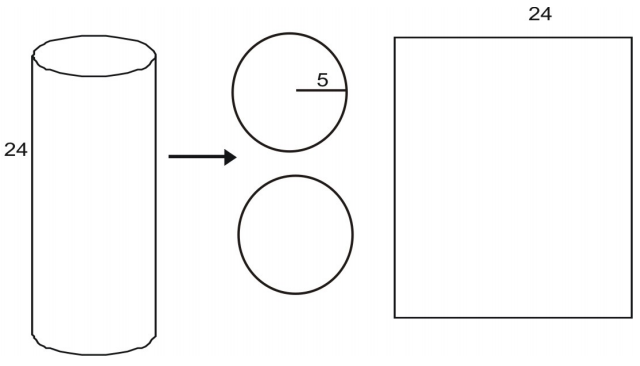 Fig2_1_21 The area of each base is given by the area of a circle:

[latex]A=\pi{r}^2\\[/latex] [latex-display]A=\pi(5)^2\\[/latex-display] [latex-display]A=25\pi\\[/latex-display] [latex]A\approx(25)(3.14)=78.5\\[/latex]

The area of the rectangular lateral area L is given by the product of a width and height. The height is given as 24. You can see that the width of the area is equal to the circumference of the circular base.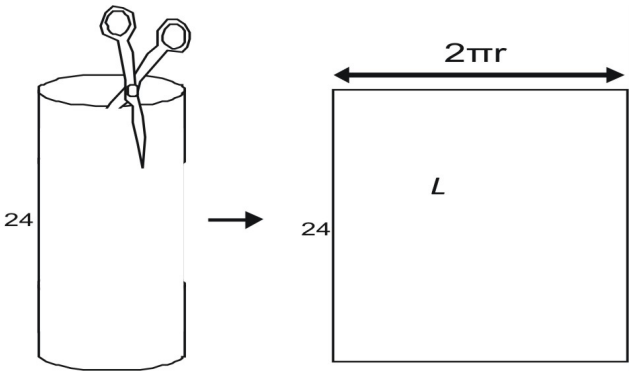 Fig2_1_22 To find the width, imagine taking a can-like cylinder apart with a scissors. When you cut the lateral area, you see that it is equal to the circumference of the can’s top. The circumference of a circle is given by C = 2πr, the lateral area, L, is

[latex]L=2{\pi}rh\\[/latex] [latex-display]L=2{\pi}(5)(24)\\[/latex-display] [latex-display]L=240\pi\\[/latex-display] [latex]L\approx(240)(3.14)=753.6\\[/latex]

Now we can find the area of the entire cylinder using A = (area of two bases) + (area of lateral side).

[latex]A=2(75.36)+753.6\\[/latex] [latex]A=904.32\\[/latex]

You can see that the formula we used to find the total surface area can be used for any right cylinder.
Area of a Right Cylinder: The surface area of a right cylinder, with radius and height h is given by A = 2B + L, where B is the area of each base of the cylinder and L is the lateral area of the cylinder.

Example 4

Use a net to find the surface area of the cylinder.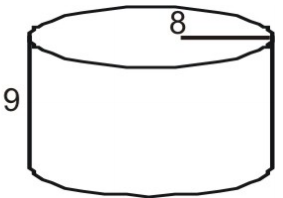 Fig2_1_23 First draw and label a net for the figure. 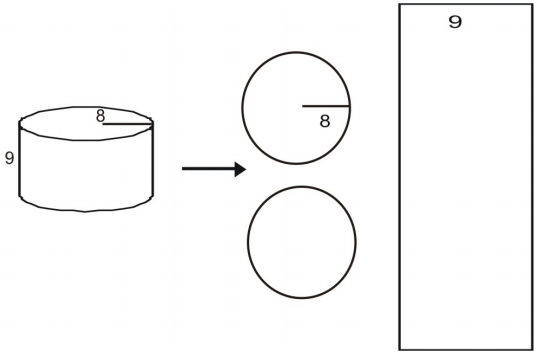Fig2_1_24 Calculate the area of each base.

[latex]A=\pi{r}^2\\[/latex] [latex-display]A=\pi(8)^2\\[/latex-display] [latex-display]A=64\pi\\[/latex-display] [latex]A\approx(64)(3.14)=200.96\\[/latex]

Calculate L.

[latex]L=2{\pi}rh\\[/latex] [latex-display]L=2{\pi}(8)(9)\\[/latex-display] [latex-display]L=144\pi\\[/latex-display] [latex]L\approx(144)(3.14)=452.16\\[/latex]

Find the area of the entire cylinder.

[latex]A=2(200.96)+452.16\\[/latex] [latex]A=854.08\\[/latex]

Thus, the total surface area is approximately 854.08 square units

Surface Area of a Cylinder Using a Formula

You have seen how to use nets to find the total surface area of a cylinder. The postulate can be broken down to create a general formula for all right cylinders. A = 2B + L Fig2_1_25 Notice that the base, B, of any cylinder is: B = πr2 The lateral area, L, for any cylinder is:

[latex]L=\text{width of lateral area}\cdot\text{height of cylinder}\\[/latex] [latex-display]L=\text{circumference of base}\cdot\text{height of cylinder}\\[/latex-display] [latex]L=2\pi{r}\cdot{h}\\[/latex]

Putting the two equations together we get: Factoring out a from the equation gives:
The Surface Area of a Right Cylinder: A right cylinder with radius r and height h can be expressed as: A = 2πr2 + 2πrh or: A = 2πr(r + h)
You can use the formulas to find the area of any right cylinder.

Example 5

Use the formula to find the surface area of the cylinder.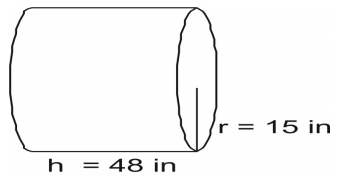 Fig2_1_26 Write the formula and substitute in the values and solve.

[latex]A=2(\pi{r}^2)+2\pi{rh}\\[/latex] [latex-display]A=2(3.14)(15)(15)+2(3.14)(15)(48)\\[/latex-display] [latex-display]A=1413+4521.6\\[/latex-display] [latex]A=5934.6\text{ square inches}\\[/latex]

Example 6

Find the surface area of the cylinder.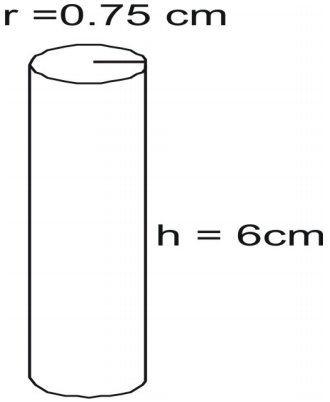 Fig2_1_27 Write the formula and substitute in the values and solve.

[latex]A=2\pi{r}(r+h)\\[/latex] [latex-display]A=2(3.14)(0.75)[0.75+6]\\[/latex-display] [latex]A=31.7925\text{ square inches}\\[/latex]

Example 7

Find the height of a cylinder that has radius 4cm and surface area of 226.08 sq cm. Write the formula with the given information and solve for h.

[latex]A=2\pi{r}(r+h)\\[/latex] [latex-display]226.08=2(3.14)(4)[4+h]\\[/latex-display] [latex-display]226.08=25.12[4+h]\\[/latex-display] [latex-display]226.08=100.48+25.12h\\[/latex-display] [latex]5=h\\[/latex]

Spheres

A sphere is a three-dimensional figure that has the shape of a ball. Fig2_1_28 Spheres can be characterized in three ways.
  • A sphere is the set of all points that lie a fixed distance r from a single center point O.
  • A sphere is the surface that results when a circle is rotated about any of its diameters.
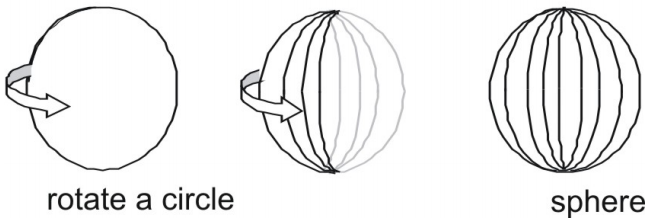
Fig2_1_29

Surface Area of a Sphere

You can infer the formula for the surface area of a sphere by taking measurements of spheres and cylinders. Here we show a sphere with a radius of 3 and a right cylinder with both a radius and a height of 3 and express the area in terms of π.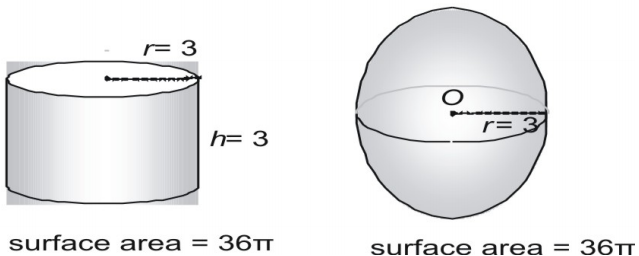 Fig2_1_30 Now try a larger pair, expressing the surface area in decimal form. 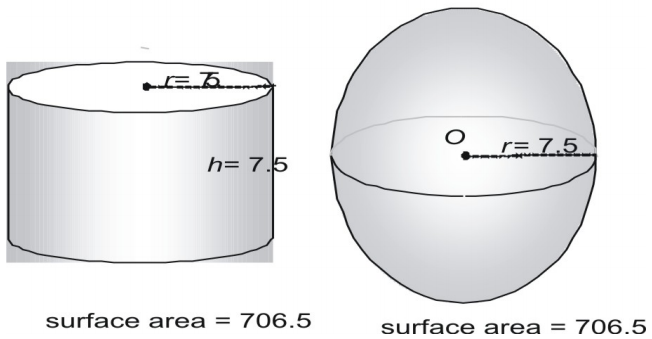Fig2_1_31 Look at a third pair. 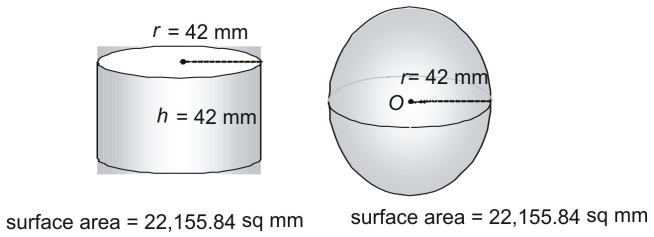Fig2_1_32 Is it a coincidence that a sphere and a cylinder whose radius and height are equal to the radius of the sphere have the exact same surface area? Not at all! In fact, the ancient Greeks used a method that showed that the following formula can be used to find the surface area of any sphere (or any cylinder in which ).
The Surface Area of a Sphere is given by: A = 4πr2

Example 8

Find the surface area of a sphere with a radius of 14 feet. Use the formula.

[latex]A=4\pi{r}^2\\[/latex] [latex-display]A=4\pi(14)^2\\[/latex-display] [latex-display]A=4\pi(196)\\[/latex-display] [latex-display]A=784\pi\\[/latex-display] [latex]2461.76\text{ square feet using }3.14\text{ for }\pi\\[/latex]

Example 9

Find the surface area of the following figure in terms of π.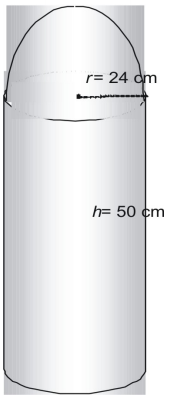 Fig2_1_33 The figure is made of one half sphere or hemisphere, and one cylinder without its top.

[latex]A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\[/latex] [latex-display]A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\[/latex-display] [latex-display]A(\text{half sphere})=2\pi(576)\\[/latex-display] [latex]A(\text{half sphere})=1152\pi\text{ square cm}\\[/latex]

Now find the area of the cylinder without its top.

[latex]A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\[/latex] [latex-display]A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\[/latex-display] [latex-display]A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\[/latex-display] [latex-display]A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\[/latex-display] [latex]A(\text{topless cylinder})=2976\pi\text{ square cm}\\[/latex]

Thus, the total surface area is [latex]1152\pi+2976\pi=4128\pi\\[/latex]

Review Exercises

  1. Find the radius of the sphere that has a volume of 335 cm3.
  2. Determine the surface area and volume of this shape: Fig2_1_34
  3. The radius of a sphere is 4. Find its volume and total surface area.
  4. A sphere has a radius of 5. A right cylinder, having the same radius has the same volume. Find the height and total surface area of the cylinder.
  5. Sphere: volume = 296 cm3. Find the Diameter.
  6. Sphere: surface area is 179 in2. Find the Radius.
  7. Tennis balls with a diameter of 3.5 inches are sold in cans of three. The can is a cylinder. Assume the balls touch the can on the sides, top and bottom. What is the volume of the space not occupied by the tennis balls?
  8. A sphere has surface area of 36π in2. Find its volume.
  9. A giant scoop, operated by a crane, is in the shape of a hemisphere of radius = 21 inches. The scoop is filled with melted hot steel. When the steel is poured into a cylindrical storage tank that has a radius of 28 inches, the melted steel will rise to a height of how many inches?

Answers

Note that these problems use π not 3.14.
  1. 1. Radius = 4.31 cm
  2. Surface area = 706.86 cm2 Volume = 1767.15 cm3
  3. Volume = 268.08 units3 Surface area = 201.06 units2
  4. Height = 20/3 units total surface area = 366.52 units2
  5. Diameter = 8.27cm
  6. Radius = 3.77 inches
  7. Volume of cylinder = 32.16π in3 volume of tennis balls = 21.44π in3 Volume of space not occupied by tennis balls = 33.68 in3
  8. Volume = 113.10 in3
  9. Height of molten steel in cylinder will be 7.88 inches

Licenses & Attributions

CC licensed content, Shared previously