Let’s revisit our friend Wally from "Area and Perimeter" and use another aspect of his yard to introduce the concept of volume. Wally is a swimmer and wants to install a lap pool in his backyard. Because he has some extra space, he is going to build a pool that is 25 yards long, 2 yards wide, and 2 yards deep. How many cubic yards of water must be used to fill the pool (assuming right to the top).
Much as we did with area (counting unit squares), with volume we will be counting unit cubes. What is the volume of a unit cube? Let’s look at figure 1:
Finding the Volume of a Cube
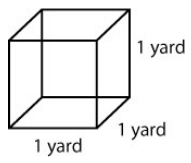
Figure 1. Volume = 1 yd × 1yd × yd = 1 cubic yard
The shape at left is a cube (all sides are equal length). In particular, because all sides are of length 1, this cube is called a unit cube.
We know the area of the base from our previous work (1 yd × 1 yd or 1 square yard). We are going to take that area and extend it vertically through a height of 1 yard so our volume becomes
Volume = 1 yd × 1yd × yd = 1 cubic yard
How does this help Wally? Well, if he can count the number of unit cubes in his pool, he can determine the volume of water needed to fill the pool.
Guided Example
Filling Wally’s Pool

Figure 2. Volume = Length × Width × Height
or V = LWH
If we fill the pool with unit cubes, we can fill 25 unit cubes along the length, 2 along the width and 2 along the height. That would give us 25 × 2 × 2 = 100 unit cubes or:
Volume = 25 yd × 2 yd × 2 yd = 100 cubic yd
Explicit formulas for the types of rectangular solids used in the previous section are as follows:
Example 3
Find the volume of a sphere with radius 5 meters.
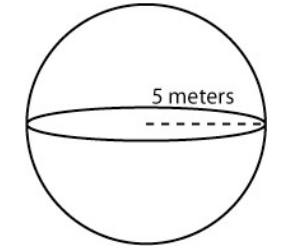
Solution
[latex-display]\displaystyle\frac{500}{3}\pi\text{ cm}^3\\[/latex-display]
Example 4
Determine the volume of each of the following. Include a drawing of the shape with the included information. Show all work. As in the examples, if units are included then units should be present in your final result. Use 3.14 for π and round answers to tenths as needed.
- Find the volume of a cube with side 3.25 meters.
- Find the volume of a box with sides of length 4 feet by [latex]\displaystyle{2}\frac{1}{2}\\[/latex] feet by 6 feet.
- Find the volume of a can with radius 4.62 cm and height 10 cm.
- Find the volume of a sphere with diameter 12 yards.
Solution
- 34.3 m3 or 34.3 cubic meters
- 60 ft3 or 60 cubic feet
- 670.2 cm3 or 670.2 cubic centimeters
- 904.3 yd3 or 904.3 cubic yards
 Figure 1. Volume = 1 yd × 1yd × yd = 1 cubic yard
Figure 1. Volume = 1 yd × 1yd × yd = 1 cubic yard Figure 2. Volume = Length × Width × Height or V = LWH
Figure 2. Volume = Length × Width × Height or V = LWH


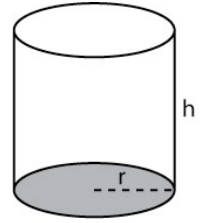 Figure 3.
Figure 3.





