Arithmetic Sequences
Companies often make large purchases, such as computers and vehicles, for business use. The book-value of these supplies decreases each year for tax purposes. This decrease in value is called depreciation. One method of calculating depreciation is straight-line depreciation, in which the value of the asset decreases by the same amount each year. As an example, consider a woman who starts a small contracting business. She purchases a new truck for $25,000. After five years, she estimates that she will be able to sell the truck for $8,000. The loss in value of the truck will therefore be $17,000, which is $3,400 per year for five years. The truck will be worth $21,600 after the first year; $18,200 after two years; $14,800 after three years; $11,400 after four years; and $8,000 at the end of five years. In this section, we will consider specific kinds of sequences that will allow us to calculate depreciation, such as the truck’s value.Terms of an Arithmetic Sequence
The values of the truck in the example are said to form an arithmetic sequence because they change by a constant amount each year. Each term increases or decreases by the same constant value called the common difference of the sequence. For this sequence, the common difference is –3,400. The sequence below is another example of an arithmetic sequence. In this case, the constant difference is 3. You can choose any term of the sequence, and add 3 to find the subsequent term.
The sequence below is another example of an arithmetic sequence. In this case, the constant difference is 3. You can choose any term of the sequence, and add 3 to find the subsequent term.

A General Note: Arithmetic Sequence
An arithmetic sequence is a sequence that has the property that the difference between any two consecutive terms is a constant. This constant is called the common difference. If [latex]{a}_{1}[/latex] is the first term of an arithmetic sequence and [latex]d[/latex] is the common difference, the sequence will be: [latex-display]\left\{{a}_{n}\right\}=\left\{{a}_{1},{a}_{1}+d,{a}_{1}+2d,{a}_{1}+3d,...\right\}[/latex-display]Example: Finding Common Differences
Is each sequence arithmetic? If so, find the common difference.- [latex]\left\{1,2,4,8,16,...\right\}[/latex]
- [latex]\left\{-3,1,5,9,13,...\right\}[/latex]
Answer: Subtract each term from the subsequent term to determine whether a common difference exists.
- The sequence is not arithmetic because there is no common difference.

- The sequence is arithmetic because there is a common difference. The common difference is 4.

Analysis of the Solution
The graph of each of these sequences is shown in Figure 1. We can see from the graphs that, although both sequences show growth, [latex]a[/latex] is not linear whereas [latex]b[/latex] is linear. Arithmetic sequences have a constant rate of change so their graphs will always be points on a line.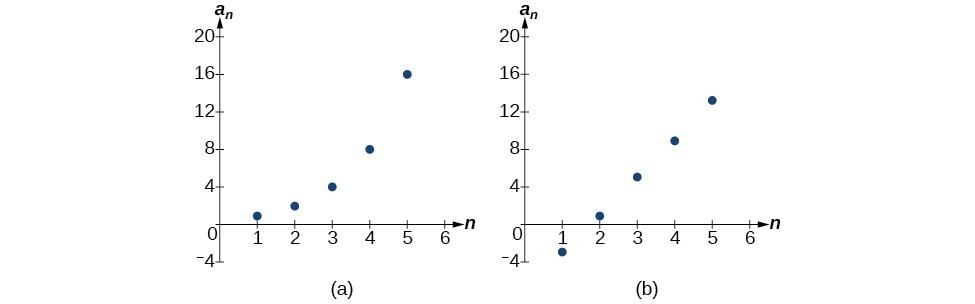
Q & A
If we are told that a sequence is arithmetic, do we have to subtract every term from the following term to find the common difference?
No. If we know that the sequence is arithmetic, we can choose any one term in the sequence, and subtract it from the subsequent term to find the common difference.Try It
Is the given sequence arithmetic? If so, find the common difference.[latex]\left\{18,\text{ }16,\text{ }14,\text{ }12,\text{ }10,\dots \right\}[/latex]
Answer: The sequence is arithmetic. The common difference is [latex]-2[/latex].
How To: Given any the first term and any other term in an arithmetic sequence, find a given term.
- Substitute the values given for [latex]{a}_{1},{a}_{n},n[/latex] into the formula [latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex] to solve for [latex]d[/latex].
- Find a given term by substituting the appropriate values for [latex]{a}_{1},n[/latex], and [latex]d[/latex] into the formula [latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex].
Example: Writing Terms of Arithmetic Sequences
Given [latex]{a}_{1}=8[/latex] and [latex]{a}_{4}=14[/latex] , find [latex]{a}_{5}[/latex] .Answer: The sequence can be written in terms of the initial term 8 and the common difference [latex]d[/latex] .
[latex]\left\{8,8+d,8+2d,8+3d\right\}[/latex]
We know the fourth term equals 14; we know the fourth term has the form [latex]{a}_{1}+3d=8+3d[/latex] . We can find the common difference [latex]d[/latex] .[latex]\begin{array}{ll}{a}_{n}={a}_{1}+\left(n - 1\right)d\hfill & \hfill \\ {a}_{4}={a}_{1}+3d\hfill & \hfill \\ {a}_{4}=8+3d\hfill & \text{Write the fourth term of the sequence in terms of } {a}_{1} \text{ and } d.\hfill \\ 14=8+3d\hfill & \text{Substitute } 14 \text{ for } {a}_{4}.\hfill \\ d=2\hfill & \text{Solve for the common difference}.\hfill \end{array}[/latex]
Find the fifth term by adding the common difference to the fourth term.[latex]{a}_{5}={a}_{4}+2=16[/latex]
Analysis of the Solution
Notice that the common difference is added to the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. The tenth term could be found by adding the common difference to the first term nine times or by using the equation [latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex].Try It
Given [latex]{a}_{3}=7[/latex] and [latex]{a}_{5}=17[/latex] , find [latex]{a}_{2}[/latex] .Answer: [latex]{a}_{2}=2[/latex]
[latex]\begin{array}{lllll}{a}_{n}={a}_{n - 1}+d\hfill & \hfill & \hfill & \hfill & n\ge 2\hfill \end{array}[/latex]
A General Note: Recursive Formula for an Arithmetic Sequence
The recursive formula for an arithmetic sequence with common difference [latex]d[/latex] is:[latex]\begin{array}{lllll}{a}_{n}={a}_{n - 1}+d\hfill & \hfill & \hfill & \hfill & n\ge 2\hfill \end{array}[/latex]
How To: Given an arithmetic sequence, write its recursive formula.
- Subtract any term from the subsequent term to find the common difference.
- State the initial term and substitute the common difference into the recursive formula for arithmetic sequences.
Example: Writing a Recursive Formula for an Arithmetic Sequence
Write a recursive formula for the arithmetic sequence. [latex-display]\left\{-18\text{, }-7\text{, }4\text{, }15\text{, }26\text{, \ldots }\right\}[/latex-display]Answer: The first term is given as [latex]-18[/latex] . The common difference can be found by subtracting the first term from the second term.
[latex]d=-7-\left(-18\right)=11[/latex]
Substitute the initial term and the common difference into the recursive formula for arithmetic sequences.[latex]\begin{array}{l}{a}_{1}=-18\hfill \\ {a}_{n}={a}_{n - 1}+11,\text{ for }n\ge 2\hfill \end{array}[/latex]
Analysis of the Solution
We see that the common difference is the slope of the line formed when we graph the terms of the sequence, as shown in Figure 3. The growth pattern of the sequence shows the constant difference of 11 units.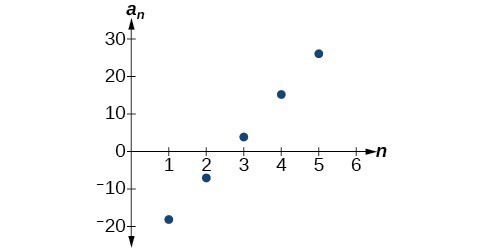
How To: Do we have to subtract the first term from the second term to find the common difference?
No. We can subtract any term in the sequence from the subsequent term. It is, however, most common to subtract the first term from the second term because it is often the easiest method of finding the common difference.Try It
Write a recursive formula for the arithmetic sequence.[latex]\left\{25\text{, } 37\text{, } 49\text{, } 61\text{, } \text{\ldots }\right\}[/latex]
Answer: [latex]\begin{array}{l}{a}_{1}=25\hfill \\ {a}_{n}={a}_{n - 1}+12,\text{ for }n\ge 2\hfill \end{array}[/latex]
Solving Application Problems with Arithmetic Sequences
In many application problems, it often makes sense to use an initial term of [latex]{a}_{0}[/latex] instead of [latex]{a}_{1}[/latex]. In these problems, we alter the explicit formula slightly to account for the difference in initial terms. We use the following formula: [latex-display]{a}_{n}={a}_{0}+dn[/latex-display]Example: Solving Application Problems with Arithmetic Sequences
A five-year old child receives an allowance of $1 each week. His parents promise him an annual increase of $2 per week.- Write a formula for the child’s weekly allowance in a given year.
- What will the child’s allowance be when he is 16 years old?
Answer:
- The situation can be modeled by an arithmetic sequence with an initial term of 1 and a common difference of 2.Let [latex]A[/latex] be the amount of the allowance and [latex]n[/latex] be the number of years after age 5. Using the altered explicit formula for an arithmetic sequence we get: [latex]{A}_{n}=1+2n[/latex]
- We can find the number of years since age 5 by subtracting. [latex-display]16 - 5=11[/latex-display] We are looking for the child’s allowance after 11 years. Substitute 11 into the formula to find the child’s allowance at age 16. [latex-display]{A}_{11}=1+2\left(11\right)=23[/latex-display] The child’s allowance at age 16 will be $23 per week.
Try It
A woman decides to go for a 10-minute run every day this week and plans to increase the time of her daily run by 4 minutes each week. Write a formula for the time of her run after n weeks. How long will her daily run be 8 weeks from today?Answer: The formula is [latex]{T}_{n}=10+4n[/latex], and it will take her 42 minutes.
Key Equations
| recursive formula for nth term of an arithmetic sequence | [latex]{a}_{n}={a}_{n - 1}+d\phantom{\rule{1}{0ex}}n\ge 2[/latex] |
| explicit formula for nth term of an arithmetic sequence | [latex]\begin{array}{l}{a}_{n}={a}_{1}+d\left(n - 1\right)\end{array}[/latex] |
Key Concepts
- An arithmetic sequence is a sequence where the difference between any two consecutive terms is a constant.
- The constant between two consecutive terms is called the common difference.
- The common difference is the number added to any one term of an arithmetic sequence that generates the subsequent term.
- The terms of an arithmetic sequence can be found by beginning with the initial term and adding the common difference repeatedly.
- A recursive formula for an arithmetic sequence with common difference [latex]d[/latex] is given by [latex]{a}_{n}={a}_{n - 1}+d,n\ge 2[/latex].
- As with any recursive formula, the initial term of the sequence must be given.
- An explicit formula for an arithmetic sequence with common difference [latex]d[/latex] is given by [latex]{a}_{n}={a}_{1}+d\left(n - 1\right)[/latex].
- An explicit formula can be used to find the number of terms in a sequence.
- In application problems, we sometimes alter the explicit formula slightly to [latex]{a}_{n}={a}_{0}+dn[/latex].
Glossary
arithmetic sequence a sequence in which the difference between any two consecutive terms is a constant common difference the difference between any two consecutive terms in an arithmetic sequenceLicenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 5847, 5832. Authored by: Web-Work Rochester. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 23735. Authored by: Roy Shahbazian. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 29759. Authored by: McClure, Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Question ID 23521. Authored by: Shahbazian,Roy, mb McClure,Caren. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Arithmetic Sequences . Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
