Systems of Linear Equations: Three Variables
John received an inheritance of $12,000 that he divided into three parts and invested in three ways: in a money-market fund paying 3% annual interest; in municipal bonds paying 4% annual interest; and in mutual funds paying 7% annual interest. John invested $4,000 more in municipal funds than in municipal bonds. He earned $670 in interest the first year. How much did John invest in each type of fund? (credit: "Elembis," Wikimedia Commons)
(credit: "Elembis," Wikimedia Commons)Solve Systems of Three Equations in Three Variables
In order to solve systems of equations in three variables, known as three-by-three systems, the primary goal is to eliminate one variable at a time to achieve back-substitution. A solution to a system of three equations in three variables [latex]\left(x,y,z\right),\text{}[/latex] is called an ordered triple. To find a solution, we can perform the following operations:- Interchange the order of any two equations.
- Multiply both sides of an equation by a nonzero constant.
- Add a nonzero multiple of one equation to another equation.
A General Note: Number of Possible Solutions
The planes illustrate possible solution scenarios for three-by-three systems.- Systems that have a single solution are those which, after elimination, result in a solution set consisting of an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex]. Graphically, the ordered triple defines a point that is the intersection of three planes in space.
- Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space.
- Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex]. Graphically, a system with no solution is represented by three planes with no point in common.
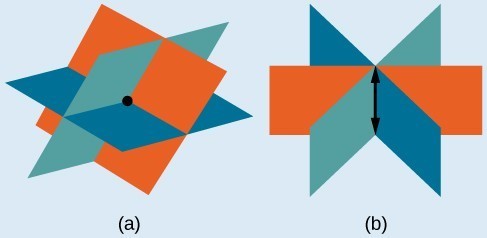 (a)Three planes intersect at a single point, representing a three-by-three system with a single solution. (b) Three planes intersect in a line, representing a three-by-three system with infinite solutions.
(a)Three planes intersect at a single point, representing a three-by-three system with a single solution. (b) Three planes intersect in a line, representing a three-by-three system with infinite solutions.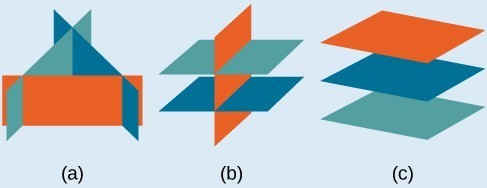
Example: Determining Whether an Ordered Triple Is a Solution to a System
Determine whether the ordered triple [latex]\left(3,-2,1\right)[/latex] is a solution to the system.[latex]\begin{array}{l}\text{ }x+y+z=2\hfill \\ 6x - 4y+5z=31\hfill \\ 5x+2y+2z=13\hfill \end{array}[/latex]
Answer: We will check each equation by substituting in the values of the ordered triple for [latex]x,y[/latex], and [latex]z[/latex].
[latex]\begin{array}{ccccc}\begin{array}{r}\hfill x+y+z=2\\ \hfill \left(3\right)+\left(-2\right)+\left(1\right)=2\\ \hfill \text{True}\end{array}& & \begin{array}{r}\hfill \text{}6x - 4y+5z=31\\ \hfill 6\left(3\right)-4\left(-2\right)+5\left(1\right)=31\\ \hfill 18+8+5=31\\ \hfill \text{True}\end{array}& & \begin{array}{r}\hfill \text{}5x+2y+2z=13\\ \hfill 5\left(3\right)+2\left(-2\right)+2\left(1\right)=13\\ \hfill \text{}15 - 4+2=13\\ \hfill \text{True}\end{array}\end{array}[/latex]
The ordered triple [latex]\left(3,-2,1\right)[/latex] is indeed a solution to the system.How To: Given a linear system of three equations, solve for three unknowns.
- Pick any pair of equations and solve for one variable.
- Pick another pair of equations and solve for the same variable.
- You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
Example: Solving a System of Three Equations in Three Variables by Elimination
Find a solution to the following system:[latex]\begin{array}{ll}\text{ }x - 2y+3z=9\hfill & \text{(1)}\hfill \\ \text{ }-x+3y-z=-6\hfill & \text{(2)}\hfill \\ 2x - 5y+5z=17\hfill & \text{(3)}\hfill \end{array}[/latex]
Answer: There will always be several choices as to where to begin, but the most obvious first step here is to eliminate [latex]x[/latex] by adding equations (1) and (2).
[latex]\frac{\begin{array}{ll}\text{ }\text{}x - 2y+3z=9\hfill & \text{(1)}\hfill \\ \text{ }-x+3y-z=-6\hfill & \text{ (2)}\hfill \end{array}}{\begin{array}{ll}\text{ }\text{}\text{}y+2z=3\hfill & \text{ (3)}\hfill \end{array}}[/latex]
The second step is multiplying equation (1) by [latex]-2[/latex] and adding the result to equation (3). These two steps will eliminate the variable [latex]x[/latex].[latex]\begin{array} \hfill−2x+4y−6z=−18 \hfill& \left(1\right)\text{ multiplied by }−2 \\ 2x−5y+5z=17 \hfill& \left(3\right) \\ \text{_____________________________} \\ \hfill−y−z=−1\left(5\right)\hfill& \end{array}[/latex]
In equations (4) and (5), we have created a new two-by-two system. We can solve for [latex]z[/latex] by adding the two equations.[latex]\frac{\begin{array}{l}\begin{array}{l}\hfill \\ \text{}y+2z=3\text{ }\left(4\right)\hfill \end{array}\hfill \\ -y-z=-1\text{ }\left(5\right)\hfill \end{array}}{z=2\text{ }\left(6\right)}[/latex]
Choosing one equation from each new system, we obtain the upper triangular form:[latex]\begin{array}{ll}\text{}\text{}x - 2y+3z=9\text{ }\hfill & \left(1\right)\hfill \\ \text{ }y+2z=3\hfill & \left(4\right)\hfill \\ \text{ }z=2\hfill & \left(6\right)\hfill \end{array}[/latex]
Next, we back-substitute [latex]z=2[/latex] into equation (4) and solve for [latex]y[/latex].[latex]\begin{array}{l}y+2\left(2\right)=3\hfill \\ \text{ }y+4=3\hfill \\ \text{ }y=-1\hfill \end{array}[/latex]
Finally, we can back-substitute [latex]z=2[/latex] and [latex]y=-1[/latex] into equation (1). This will yield the solution for [latex]x[/latex].[latex]\begin{array}{r}\hfill x - 2\left(-1\right)+3\left(2\right)=9\\ \hfill \text{ }x+2+6=9\\ \hfill \text{ }x=1\end{array}[/latex]
The solution is the ordered triple [latex]\left(1,-1,2\right)[/latex].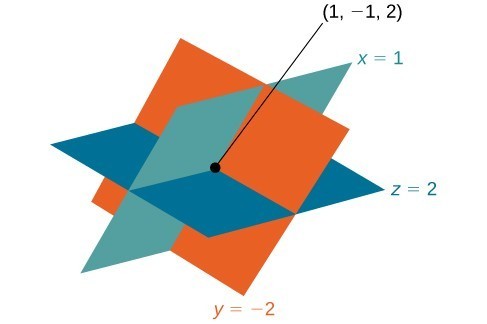
Try It
Solve the system of equations in three variables.[latex]\begin{array}{l}2x+y - 2z=-1\hfill \\ 3x - 3y-z=5\hfill \\ x - 2y+3z=6\hfill \end{array}[/latex]
Answer: [latex]\left(1,-1,1\right)[/latex]
Key Concepts
- A solution set is an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex] that represents the intersection of three planes in space.
- A system of three equations in three variables can be solved by using a series of steps that forces a variable to be eliminated. The steps include interchanging the order of equations, multiplying both sides of an equation by a nonzero constant, and adding a nonzero multiple of one equation to another equation.
- Systems of three equations in three variables are useful for solving many different types of real-world problems.
- A system of equations in three variables is inconsistent if no solution exists. After performing elimination operations, the result is a contradiction.
- Systems of equations in three variables that are inconsistent could result from three parallel planes, two parallel planes and one intersecting plane, or three planes that intersect the other two but not at the same location.
- A system of equations in three variables is dependent if it has an infinite number of solutions. After performing elimination operations, the result is an identity.
- Systems of equations in three variables that are dependent could result from three identical planes, three planes intersecting at a line, or two identical planes that intersect the third on a line.
Glossary
solution set the set of all ordered pairs or triples that satisfy all equations in a system of equationsLicenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. License: CC BY: Attribution. License terms: Download for free at http://cnx.org/contents/[email protected].
- Question ID 23765, 29695. Authored by: Roy Shahbazian. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
- Systems of Equations in Three Variables: Part 1 of 2. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
