We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Complex Numbers

Learning Outcomes

By the end of this lesson, you will be able to:
  • Express square roots of negative numbers as multiples of i.
  • Plot complex numbers on the complex plane.
  • Add and subtract complex numbers.
  • Multiply and divide complex numbers.

The study of mathematics continuously builds upon itself. Negative integers, for example, fill a void left by the set of positive integers. The set of rational numbers, in turn, fills a void left by the set of integers. The set of real numbers fills a void left by the set of rational numbers. Not surprisingly, the set of real numbers has voids as well. For example, we still have no solution to equations such as

[latex]{x}^{2}+4=0[/latex]

Our best guesses might be +2 or –2. But if we test +2 in this equation, it does not work. If we test –2, it does not work. If we want to have a solution for this equation, we will have to go farther than we have so far. After all, to this point we have described the square root of a negative number as undefined. Fortunately, there is another system of numbers that provides solutions to problems such as these. In this section, we will explore this number system and how to work within it.

Express square roots of negative numbers as multiples of i

We know how to find the square root of any positive real number. In a similar way, we can find the square root of a negative number. The difference is that the root is not real. If the value in the radicand is negative, the root is said to be an imaginary number. The imaginary number [latex]i[/latex] is defined as the square root of negative 1.

[latex]\sqrt{-1}=i[/latex]

So, using properties of radicals,

[latex]{i}^{2}={\left(\sqrt{-1}\right)}^{2}=-1[/latex]

We can write the square root of any negative number as a multiple of i. Consider the square root of –25.

[latex]\begin{align} \sqrt{-25}&=\sqrt{25\cdot \left(-1\right)} \\ &=\sqrt{25}\sqrt{-1} \\ &=5i \end{align}[/latex]

We use 5i and not [latex]-\text{5}i[/latex] because the principal root of 25 is the positive root.

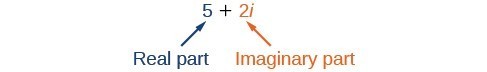Showing the real and imaginary parts of 5 + 2i. In this complex number, 5 is the real part and 2i is the complex part. Figure 1

A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written a + bi where a is the real part and bi is the imaginary part. For example, [latex]5+2i[/latex] is a complex number. So, too, is [latex]3+4\sqrt{3}i[/latex].

Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.

A General Note: Imaginary and Complex Numbers

A complex number is a number of the form [latex]a+bi[/latex] where

  • a is the real part of the complex number.
  • bi is the imaginary part of the complex number.

If [latex]b=0[/latex], then [latex]a+bi[/latex] is a real number. If [latex]a=0[/latex] and b is not equal to 0, the complex number is called an imaginary number. An imaginary number is an even root of a negative number.

How To: Given an imaginary number, express it in standard form.

  1. Write [latex]\sqrt{-a}[/latex] as [latex]\sqrt{a}\sqrt{-1}[/latex].
  2. Express [latex]\sqrt{-1}[/latex] as i.
  3. Write [latex]\sqrt{a}\cdot i[/latex] in simplest form.

Example 1: Expressing an Imaginary Number in Standard Form

Express [latex]\sqrt{-9}[/latex] in standard form.

Answer:

[latex]\sqrt{-9}=\sqrt{9}\sqrt{-1}=3i[/latex]

In standard form, this is [latex]0+3i[/latex].

Try It 1

Express [latex]\sqrt{-24}[/latex] in standard form.

Answer: [latex-display]\sqrt{-24}=0+2\sqrt{6} \cdot i[/latex-display]

Try it 2

[ohm_question hide_question_numbers=1]174132[/ohm_question]

 Add and subtract complex numbers

Just as with real numbers, we can perform arithmetic operations on complex numbers. To add or subtract complex numbers, we combine the real parts and combine the imaginary parts.

A General Note: Addition and Subtraction of Complex Numbers

Adding complex numbers:

[latex]\left(a+bi\right)+\left(c+di\right)=\left(a+c\right)+\left(b+d\right)i[/latex]

Subtracting complex numbers:

[latex]\left(a+bi\right)-\left(c+di\right)=\left(a-c\right)+\left(b-d\right)i[/latex]

How To: Given two complex numbers, find the sum or difference.

  1. Identify the real and imaginary parts of each number.
  2. Add or subtract the real parts.
  3. Add or subtract the imaginary parts.

Example 3: Adding Complex Numbers

Add [latex]3 - 4i[/latex] and [latex]2+5i[/latex].

Answer:

We add the real parts and add the imaginary parts.

[latex]\begin{align}\left(a+bi\right)+\left(c+di\right)&=\left(a+c\right)+\left(b+d\right)i \\ \left(3 - 4i\right)+\left(2+5i\right)&=\left(3+2\right)+\left(-4+5\right)i \\ &=5+i \end{align}[/latex]

Try It 3

Subtract [latex]2+5i[/latex] from [latex]3 - 4i[/latex].

Answer: [latex-display]\left(3 - 4i\right)-\left(2+5i\right)=1 - 9i[/latex-display]

try it 4

[ohm_question hide_question_numbers=1]104014[/ohm_question]

Multiplying Complex Numbers

Multiplying complex numbers is much like multiplying binomials. The major difference is that we work with the real and imaginary parts separately.

Multiplying a Complex Number by a Real Number

Let’s begin by multiplying a complex number by a real number. We distribute the real number just as we would with a binomial. So, for example,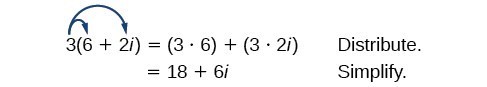
Showing how distribution works for complex numbers. For 3(6+2i), 3 is multiplied to both the real and imaginary parts. So we have (3)(6)+(3)(2i) = 18 + 6i. Figure 5

How To: Given a complex number and a real number, multiply to find the product.

  1. Use the distributive property.
  2. Simplify.

Example 4: Multiplying a Complex Number by a Real Number

Find the product [latex]4\left(2+5i\right)[/latex].

Answer:

Distribute the 4.

[latex]\begin{align}4\left(2+5i\right)&=\left(4\cdot 2\right)+\left(4\cdot 5i\right) \\ &=8+20i \end{align}[/latex]

Try It 5

Find the product [latex]-4\left(2+6i\right)[/latex].

Answer: [latex-display]-8 - 24i[/latex-display]

Multiplying Complex Numbers Together

Now, let’s multiply two complex numbers. We can use either the distributive property or the FOIL method. Recall that FOIL is an acronym for multiplying First, Outer, Inner, and Last terms together. Using either the distributive property or the FOIL method, we get

[latex]\left(a+bi\right)\left(c+di\right)=ac+adi+bci+bd{i}^{2}[/latex]

Because [latex]{i}^{2}=-1[/latex], we have

[latex]\left(a+bi\right)\left(c+di\right)=ac+adi+bci-bd[/latex]

To simplify, we combine the real parts, and we combine the imaginary parts.

[latex]\left(a+bi\right)\left(c+di\right)=\left(ac-bd\right)+\left(ad+bc\right)i[/latex]

How To: Given two complex numbers, multiply to find the product.

  1. Use the distributive property or the FOIL method.
  2. Simplify.

Example 5: Multiplying a Complex Number by a Complex Number

Multiply [latex]\left(4+3i\right)\left(2 - 5i\right)[/latex].

Answer:

[latex]\begin{align}\left(4+3i\right)\left(2 - 5i\right)&=4\cdot 2 +4\cdot (-5i) + 3i \cdot 2 +3i \cdot (-5i) \\ &=8 - 20i + 6i - 15i^2 \\ &=8 - 14i -15(-1) \\ &=8-14i+15 \\ &=23 - 14i \end{align}[/latex]

Try It 6

Multiply [latex]\left(3 - 4i\right)\left(2+3i\right)[/latex].

Answer: [latex-display]18+i[/latex-display]

try it 7

[ohm_question hide_question_numbers=1]151095[/ohm_question]

Dividing Complex Numbers

Division of two complex numbers is more complicated than addition, subtraction, and multiplication because we cannot divide by an imaginary number, meaning that any fraction must have a real-number denominator. We need to find a term by which we can multiply the numerator and the denominator that will eliminate the imaginary portion of the denominator so that we end up with a real number as the denominator. This term is called the complex conjugate of the denominator, which is found by changing the sign of the imaginary part of the complex number. In other words, the complex conjugate of [latex]a+bi[/latex] is [latex]a-bi[/latex].

Note that complex conjugates have a reciprocal relationship: The complex conjugate of [latex]a+bi[/latex] is [latex]a-bi[/latex], and the complex conjugate of [latex]a-bi[/latex] is [latex]a+bi[/latex]. Further, when a quadratic equation with real coefficients has complex solutions, the solutions are always complex conjugates of one another.

Suppose we want to divide [latex]c+di[/latex] by [latex]a+bi[/latex], where neither a nor b equals zero. We first write the division as a fraction, then find the complex conjugate of the denominator, and multiply.

[latex]\begin{align} \frac{c+di}{a+bi} &= \frac{\left(c+di\right)\left(a-bi\right)}{\left(a+bi\right)\left(a-bi\right)}&&\text{Multiply the numerator and denominator by the complex conjugate of the denominator.} \\ &=\frac{ca-cbi+adi-bd{i}^{2}}{{a}^{2}-abi+abi-{b}^{2}{i}^{2}} && \text{Apply the distributive property.} \\&=\frac{ca-cbi+adi-bd\left(-1\right)}{{a}^{2}-abi+abi-{b}^{2}\left(-1\right)} && \text{Simplify, remembering that } i^2 = -1 \\ &= \frac{\left(ca+bd\right)+\left(ad-cb\right)i}{{a}^{2}+{b}^{2}} \end{align}[/latex]

A General Note: The Complex Conjugate

The complex conjugate of a complex number [latex]a+bi[/latex] is [latex]a-bi[/latex]. It is found by changing the sign of the imaginary part of the complex number. The real part of the number is left unchanged.

  • When a complex number is multiplied by its complex conjugate, the result is a real number. [latex](a+bi)(a-bi)=a^2-abi+abi-b^2i^2=a^2-b^2*(-1)=a^2+b^2[/latex]
  • When a complex number is added to its complex conjugate, the result is a real number. [latex](a+bi)+(a-bi)=2a[/latex]

Example 6: Finding Complex Conjugates

Find the complex conjugate of each number.

  1. [latex]2+i\sqrt{5}[/latex]
  2. [latex]-\frac{1}{2}i[/latex]

Answer:

  1. The number is already in the form [latex]a+bi[/latex]. The complex conjugate is [latex]a-bi[/latex], or [latex]2-i\sqrt{5}[/latex].
  2. We can rewrite this number in the form [latex]a+bi[/latex] as [latex]0-\frac{1}{2}i[/latex]. The complex conjugate is [latex]a-bi[/latex], or [latex]0+\frac{1}{2}i[/latex]. This can be written simply as [latex]\frac{1}{2}i[/latex].

Analysis of the Solution

Although we have seen that we can find the complex conjugate of an imaginary number, in practice we generally find the complex conjugates of only complex numbers with both a real and an imaginary component. To obtain a real number from an imaginary number, we can simply multiply by i.

How To: Given two complex numbers, divide one by the other.

  1. Write the division problem as a fraction.
  2. Determine the complex conjugate of the denominator.
  3. Multiply the numerator and denominator of the fraction by the complex conjugate of the denominator.
  4. Simplify.

Example 7: Dividing Complex Numbers

Divide [latex]\left(2+5i\right)[/latex] by [latex]\left(4-i\right)[/latex].

Answer:

We begin by writing the problem as a fraction. Then we multiply the numerator and denominator by the complex conjugate of the denominator.

[latex]\begin{align}\frac{\left(2+5i\right)}{\left(4-i\right)}&=\frac{\left(2+5i\right)}{\left(4-i\right)}\cdot \frac{\left(4+i\right)}{\left(4+i\right)}\\ &=\frac{8+2i+20i+5{i}^{2}}{16+4i - 4i-{i}^{2}} \\ &=\frac{8+2i+20i+5\left(-1\right)}{16+4i - 4i-\left(-1\right)} && \text{Because } {i}^{2}=-1 \\ &=\frac{3+22i}{17} \\ &=\frac{3}{17}+\frac{22}{17}i && \text{Separate real and imaginary parts}. \end{align}[/latex]

Note that this expresses the quotient in standard form.

Example 8: Substituting a Complex Number into a Polynomial Function

Let [latex]f\left(x\right)={x}^{2}-5x+2[/latex]. Evaluate [latex]f\left(3+i\right)[/latex].

Answer: Substitute [latex]x=3+i[/latex] into the function [latex]f\left(x\right)={x}^{2}-5x+2[/latex] and simplify.

[latex]\begin{align}f(3+i)&=(3+i)^2-5(3+i)+2 &&\text{Substitute } 3+i \text{ for } x. \\ &=(9+6i+i^2)-15-5i+2 &&\text{Multiply.} \\ &= 9+6i-1-15-5i+2 && \text{Substitue -1 for } i^2. \\ &=-5+i &&\text{Combine like terms.} \end{align}[/latex]

Analysis of the Solution

We write [latex]f\left(3+i\right)=-5+i[/latex]. Notice that the input is [latex]3+i[/latex] and the output is [latex]-5+i[/latex].

Try It 8

Let [latex]f\left(x\right)=2{x}^{2}-3x[/latex]. Evaluate [latex]f\left(8-i\right)[/latex].

Answer: [latex-display]102 - 29i[/latex-display]

Example 9: Substituting an Imaginary Number in a Rational Function

Let [latex]f\left(x\right)=\frac{2+x}{x+3}[/latex]. Evaluate [latex]f\left(10i\right)[/latex].

Answer:

Substitute [latex]x=10i[/latex] and simplify.

[latex]\begin{align}f(10i)&=\frac{2+10i}{10i+3} && \text{Substitute }10i\text{ for }x. \\ &=\frac{2+10i}{3+10i} && \text{Rewrite the denominator in standard form}. \\ &=\frac{2+10i}{3+10i}\cdot \frac{3 - 10i}{3 - 10i} && \text{Multiply the numerator and denominator by} \\ &&& \text{the complex conjugate of the denominator.} \\ &=\frac{6 - 20i+30i - 100{i}^{2}}{9 - 30i+30i - 100{i}^{2}} && \text{Multiply.} \\ &=\frac{6 - 20i+30i - 100\left(-1\right)}{9 - 30i+30i - 100\left(-1\right)} && \text{Substitute }-1\text{ for } {i}^{2}. \\ &=\frac{106+10i}{109} && \text{Simplify}. \\ &=\frac{106}{109}+\frac{10}{109}i && \text{Separate the real and imaginary parts}. \end{align}[/latex]

Try It 9

Let [latex]f\left(x\right)=\frac{x+1}{x - 4}[/latex]. Evaluate [latex]f\left(-i\right)[/latex].

Answer: [latex-display]-\frac{3}{17}+\frac{5i}{17}[/latex-display]

Simplifying Powers of i

The powers of i are cyclic. Let’s look at what happens when we raise i to increasing powers.

[latex]\begin{align}&{i}^{1}=i\\ &{i}^{2}=-1\\ &{i}^{3}={i}^{2}\cdot i=-1\cdot i=-i\\ &{i}^{4}={i}^{3}\cdot i=-i\cdot i=-{i}^{2}=-\left(-1\right)=1\\ &{i}^{5}={i}^{4}\cdot i=1\cdot i=i\end{align}[/latex]

We can see that when we get to the fifth power of i, it is equal to the first power. As we continue to multiply i by itself for increasing powers, we will see a cycle of 4. Let’s examine the next 4 powers of i.

[latex]\begin{align}&{i}^{6}={i}^{5}\cdot i=i\cdot i={i}^{2}=-1\\ &{i}^{7}={i}^{6}\cdot i={i}^{2}\cdot i={i}^{3}=-i\\ &{i}^{8}={i}^{7}\cdot i={i}^{3}\cdot i={i}^{4}=1\\ &{i}^{9}={i}^{8}\cdot i={i}^{4}\cdot i={i}^{5}=i\end{align}[/latex]

Example 10: Simplifying Powers of i

Evaluate [latex]{i}^{35}[/latex].

Answer:

Since [latex]{i}^{4}=1[/latex], we can simplify the problem by factoring out as many factors of [latex]{i}^{4}[/latex] as possible. To do so, first determine how many times 4 goes into 35: [latex]35=4\cdot 8+3[/latex].

[latex]{i}^{35}={i}^{4\cdot 8+3}={i}^{4\cdot 8}\cdot {i}^{3}={\left({i}^{4}\right)}^{8}\cdot {i}^{3}={1}^{8}\cdot {i}^{3}={i}^{3}=-i[/latex]

Key Concepts

  • The square root of any negative number can be written as a multiple of i.
  • To plot a complex number, we use two number lines, crossed to form the complex plane. The horizontal axis is the real axis, and the vertical axis is the imaginary axis.
  • Complex numbers can be added and subtracted by combining the real parts and combining the imaginary parts.
  • Complex numbers can be multiplied and divided.
  • To multiply complex numbers, distribute just as with polynomials.
  • To divide complex numbers, multiply both the numerator and denominator by the complex conjugate of the denominator to eliminate the complex number from the denominator.
  • The powers of i are cyclic, repeating every fourth one.

Glossary

complex conjugate
the complex number in which the sign of the imaginary part is changed and the real part of the number is left unchanged; when added to or multiplied by the original complex number, the result is a real number
complex number
the sum of a real number and an imaginary number, written in the standard form a + bi, where a is the real part, and bi is the imaginary part
complex plane
a coordinate system in which the horizontal axis is used to represent the real part of a complex number and the vertical axis is used to represent the imaginary part of a complex number
imaginary number
a number in the form bi where [latex]i=\sqrt{-1}[/latex]

Section Exercises

1. Explain how to add complex numbers. 2. What is the basic principle in multiplication of complex numbers? 3. Give an example to show the product of two imaginary numbers is not always imaginary. 4. What is a characteristic of the plot of a real number in the complex plane? For the following exercises, evaluate the algebraic expressions. 5. [latex]\text{If }f\left(x\right)={x}^{2}+x - 4[/latex], evaluate [latex]f\left(2i\right)[/latex]. 6. [latex]\text{If }f\left(x\right)={x}^{3}-2[/latex], evaluate [latex]f\left(i\right)[/latex]. 7. [latex]\text{If }f\left(x\right)={x}^{2}+3x+5[/latex], evaluate [latex]f\left(2+i\right)[/latex]. 8. [latex]\text{If }f\left(x\right)=2{x}^{2}+x - 3[/latex], evaluate [latex]f\left(2 - 3i\right)[/latex]. 9. [latex]\text{If }f\left(x\right)=\frac{x+1}{2-x}[/latex], evaluate [latex]f\left(5i\right)[/latex]. 10. [latex]\text{If }f\left(x\right)=\frac{1+2x}{x+3}[/latex], evaluate [latex]f\left(4i\right)[/latex]. For the following exercises, determine the number of real and nonreal solutions for each quadratic function shown. 11.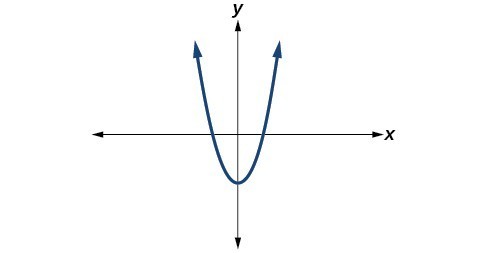 Graph of a parabola intersecting the real axis. 12. 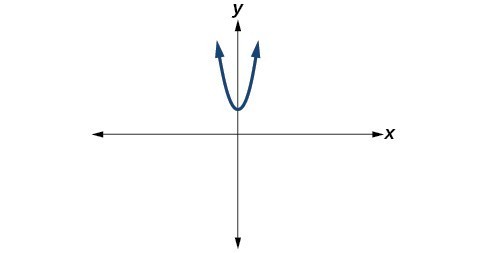Graph of a parabola not intersecting the real axis. For the following exercises, plot the complex numbers on the complex plane. 13. [latex]1 - 2i[/latex] 14. [latex]-2+3i[/latex] 15. i 16. [latex]-3 - 4i[/latex] For the following exercises, perform the indicated operation and express the result as a simplified complex number. 17. [latex]\left(3+2i\right)+\left(5 - 3i\right)[/latex] 18. [latex]\left(-2 - 4i\right)+\left(1+6i\right)[/latex] 19. [latex]\left(-5+3i\right)-\left(6-i\right)[/latex] 20. [latex]\left(2 - 3i\right)-\left(3+2i\right)[/latex] 21. [latex]\left(-4+4i\right)-\left(-6+9i\right)[/latex] 22. [latex]\left(2+3i\right)\left(4i\right)[/latex] 23. [latex]\left(5 - 2i\right)\left(3i\right)[/latex] 24. [latex]\left(6 - 2i\right)\left(5\right)[/latex] 25. [latex]\left(-2+4i\right)\left(8\right)[/latex] 26. [latex]\left(2+3i\right)\left(4-i\right)[/latex] 27. [latex]\left(-1+2i\right)\left(-2+3i\right)[/latex] 28. [latex]\left(4 - 2i\right)\left(4+2i\right)[/latex] 29. [latex]\left(3+4i\right)\left(3 - 4i\right)[/latex] 30. [latex]\frac{3+4i}{2}[/latex] 31. [latex]\frac{6 - 2i}{3}[/latex] 32. [latex]\frac{-5+3i}{2i}[/latex] 33. [latex]\frac{6+4i}{i}[/latex] 34. [latex]\frac{2 - 3i}{4+3i}[/latex] 35. [latex]\frac{3+4i}{2-i}[/latex] 36. [latex]\frac{2+3i}{2 - 3i}[/latex] 37. [latex]\sqrt{-9}+3\sqrt{-16}[/latex] 38. [latex]-\sqrt{-4}-4\sqrt{-25}[/latex] 39. [latex]\frac{2+\sqrt{-12}}{2}[/latex] 40. [latex]\frac{4+\sqrt{-20}}{2}[/latex] 41. [latex]{i}^{8}[/latex] 42. [latex]{i}^{15}[/latex] 43. [latex]{i}^{22}[/latex] For the following exercises, use a calculator to help answer the questions. 44. Evaluate [latex]{\left(1+i\right)}^{k}[/latex] for [latex]k=\text{4, 8, and 12}\text{.}[/latex] Predict the value if [latex]k=16[/latex]. 45. Evaluate [latex]{\left(1-i\right)}^{k}[/latex] for [latex]k=\text{2, 6, and 10}\text{.}[/latex] Predict the value if [latex]k=14[/latex]. 46. Evaluate [latex]\left(1+i\right)^{k}-\left(1-i\right)^{k}[/latex] for [latex]k=\text{4, 8, and 12}[/latex]. Predict the value for [latex]k=16[/latex]. 47. Show that a solution of [latex]{x}^{6}+1=0[/latex] is [latex]\frac{\sqrt{3}}{2}+\frac{1}{2}i[/latex]. 48. Show that a solution of [latex]{x}^{8}-1=0[/latex] is [latex]\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i[/latex]. For the following exercises, evaluate the expressions, writing the result as a simplified complex number. 49. [latex]\frac{1}{i}+\frac{4}{{i}^{3}}[/latex] 50. [latex]\frac{1}{{i}^{11}}-\frac{1}{{i}^{21}}[/latex] 51. [latex]{i}^{7}\left(1+{i}^{2}\right)[/latex] 52. [latex]{i}^{-3}+5{i}^{7}[/latex] 53. [latex]\frac{\left(2+i\right)\left(4 - 2i\right)}{\left(1+i\right)}[/latex] 54. [latex]\frac{\left(1+3i\right)\left(2 - 4i\right)}{\left(1+2i\right)}[/latex] 55. [latex]\frac{{\left(3+i\right)}^{2}}{{\left(1+2i\right)}^{2}}[/latex] 56. [latex]\frac{3+2i}{2+i}+\left(4+3i\right)[/latex] 57. [latex]\frac{4+i}{i}+\frac{3 - 4i}{1-i}[/latex] 58. [latex]\frac{3+2i}{1+2i}-\frac{2 - 3i}{3+i}[/latex]