We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Section Exercises

1. Explain the advantage of writing a quadratic function in standard form. 2. How can the vertex of a parabola be used in solving real world problems? 3. Explain why the condition of [latex]a\ne 0\\[/latex] is imposed in the definition of the quadratic function. 4. What is another name for the standard form of a quadratic function? 5. What two algebraic methods can be used to find the horizontal intercepts of a quadratic function? For the following exercises, rewrite the quadratic functions in standard form and give the vertex. 6. [latex]f\left(x\right)={x}^{2}-12x+32\\[/latex] 7. [latex]g\left(x\right)={x}^{2}+2x - 3\\[/latex] 8. [latex]f\left(x\right)={x}^{2}-x\\[/latex] 9. [latex]f\left(x\right)={x}^{2}+5x - 2\\[/latex] 10. [latex]h\left(x\right)=2{x}^{2}+8x - 10\\[/latex] 11. [latex]k\left(x\right)=3{x}^{2}-6x - 9\\[/latex] 12. [latex]f\left(x\right)=2{x}^{2}-6x\\[/latex] 13. [latex]f\left(x\right)=3{x}^{2}-5x - 1\\[/latex] For the following exercises, determine whether there is a minimum or maximum value to each quadratic function. Find the value and the axis of symmetry. 14. [latex]y\left(x\right)=2{x}^{2}+10x+12\\[/latex] 15. [latex]f\left(x\right)=2{x}^{2}-10x+4\\[/latex] 16. [latex]f\left(x\right)=-{x}^{2}+4x+3\\[/latex] 17. [latex]f\left(x\right)=4{x}^{2}+x - 1\\[/latex] 18. [latex]h\left(t\right)=-4{t}^{2}+6t - 1\\[/latex] 19. [latex]f\left(x\right)=\frac{1}{2}{x}^{2}+3x+1\\[/latex] 20. [latex]f\left(x\right)=-\frac{1}{3}{x}^{2}-2x+3\\[/latex] For the following exercises, determine the domain and range of the quadratic function. 21. [latex]f\left(x\right)={\left(x - 3\right)}^{2}+2\\[/latex] 22. [latex]f\left(x\right)=-2{\left(x+3\right)}^{2}-6\\[/latex] 23. [latex]f\left(x\right)={x}^{2}+6x+4\\[/latex] 24. [latex]f\left(x\right)=2{x}^{2}-4x+2\\[/latex] 25. [latex]k\left(x\right)=3{x}^{2}-6x - 9\\[/latex] For the following exercises, solve the equations over the complex numbers. 26. [latex]{x}^{2}=-25\\[/latex] 27. [latex]{x}^{2}=-8\\[/latex] 28. [latex]{x}^{2}+36=0\\[/latex] 29. [latex]{x}^{2}+27=0\\[/latex] 30. [latex]{x}^{2}+2x+5=0\\[/latex] 31. [latex]{x}^{2}-4x+5=0\\[/latex] 32. [latex]{x}^{2}+8x+25=0\\[/latex] 33. [latex]{x}^{2}-4x+13=0\\[/latex] 34. [latex]{x}^{2}+6x+25=0\\[/latex] 35. [latex]{x}^{2}-10x+26=0\\[/latex] 36. [latex]{x}^{2}-6x+10=0\\[/latex] 37. [latex]x\left(x - 4\right)=20\\[/latex] 38. [latex]x\left(x - 2\right)=10\\[/latex] 39. [latex]2{x}^{2}+2x+5=0\\[/latex] 40. [latex]5{x}^{2}-8x+5=0\\[/latex] 41. [latex]5{x}^{2}+6x+2=0\\[/latex] 42. [latex]2{x}^{2}-6x+5=0\\[/latex] 43. [latex]{x}^{2}+x+2=0\\[/latex] 44. [latex]{x}^{2}-2x+4=0\\[/latex] For the following exercises, use the vertex (h, k) and a point on the graph (x, y) to find the general form of the equation of the quadratic function. 45. [latex]\left(h,k\right)=\left(2,0\right),\left(x,y\right)=\left(4,4\right)\\[/latex] 46. [latex]\left(h,k\right)=\left(-2,-1\right),\left(x,y\right)=\left(-4,3\right)\\[/latex] 47. [latex]\left(h,k\right)=\left(0,1\right),\left(x,y\right)=\left(2,5\right)\\[/latex] 48. [latex]\left(h,k\right)=\left(2,3\right),\left(x,y\right)=\left(5,12\right)\\[/latex] 49. [latex]\left(h,k\right)=\left(-5,3\right),\left(x,y\right)=\left(2,9\right)\\[/latex] 50. [latex]\left(h,k\right)=\left(3,2\right),\left(x,y\right)=\left(10,1\right)\\[/latex] 51. [latex]\left(h,k\right)=\left(0,1\right),\left(x,y\right)=\left(1,0\right)\\[/latex] 52. [latex]\left(h,k\right)=\left(1,0\right),\left(x,y\right)=\left(0,1\right)\\[/latex] For the following exercises, sketch a graph of the quadratic function and give the vertex, axis of symmetry, and intercepts. 53. [latex]f\left(x\right)={x}^{2}-2x\\[/latex] 54. [latex]f\left(x\right)={x}^{2}-6x - 1\\[/latex] 55. [latex]f\left(x\right)={x}^{2}-5x - 6\\[/latex] 56. [latex]f\left(x\right)={x}^{2}-7x+3\\[/latex] 57. [latex]f\left(x\right)=-2{x}^{2}+5x - 8\\[/latex] 58. [latex]f\left(x\right)=4{x}^{2}-12x - 3\\[/latex] For the following exercises, write the equation for the graphed function. 59.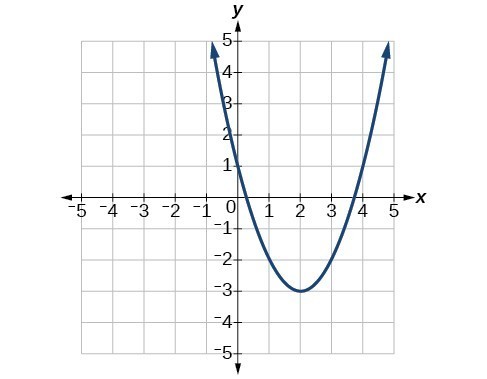 Graph of a positive parabola with a vertex at (2, -3) and y-intercept at (0, 1). 60. 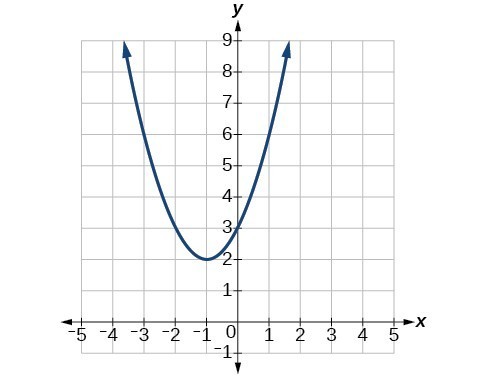Graph of a positive parabola with a vertex at (-1, 2) and y-intercept at (0, 3) 61. 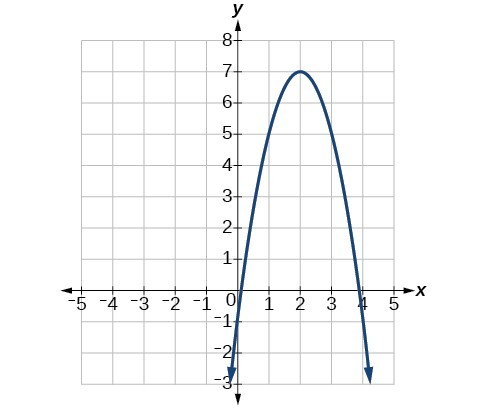Graph of a negative parabola with a vertex at (2, 7). 62. 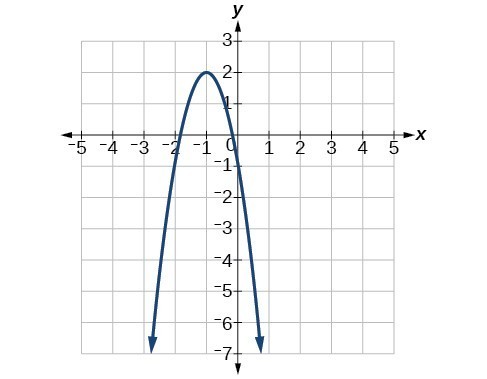Graph of a negative parabola with a vertex at (-1, 2). 63. 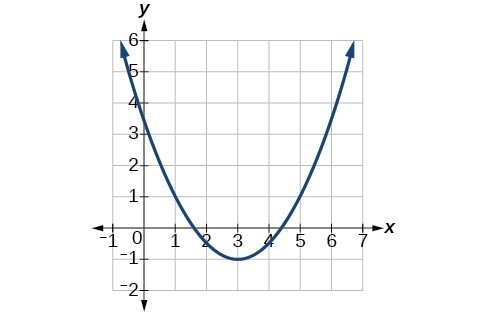Graph of a positive parabola with a vertex at (3, -1) and y-intercept at (0, 3.5). 64. 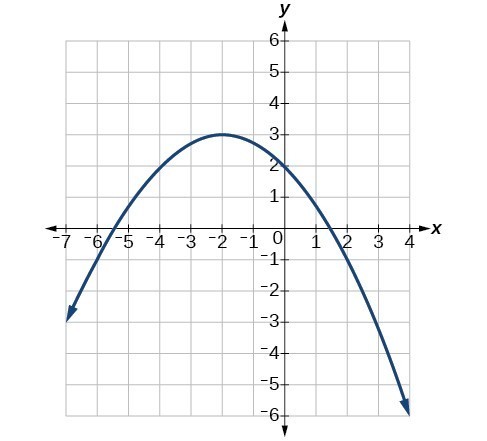Graph of a negative parabola with a vertex at (-2, 3). For the following exercises, use the table of values that represent points on the graph of a quadratic function. By determining the vertex and axis of symmetry, find the general form of the equation of the quadratic function. 65.
x –2 –1 0 1 2
y 5 2 1 2 5
66.
x –2 –1 0 1 2
y 1 0 1 4 9
67.
x –2 –1 0 1 2
y –2 1 2 1 –2
68.
x –2 –1 0 1 2
y –8 –3 0 1 0
69.
x –2 –1 0 1 2
y 8 2 0 2 8
For the following exercises, use a calculator to find the answer. 70. Graph on the same set of axes the functions [latex]f\left(x\right)={x}^{2},f\left(x\right)=2{x}^{2},\text{ and }f\left(x\right)=\frac{1}{3}{x}^{2}\\[/latex]. What appears to be the effect of changing the coefficient? 71. Graph on the same set of axes [latex]f\left(x\right)={x}^{2},f\left(x\right)={x}^{2}+2\\[/latex] and [latex]f\left(x\right)={x}^{2},f\left(x\right)={x}^{2}+5\\[/latex] and [latex]f\left(x\right)={x}^{2}-3\\[/latex]. What appears to be the effect of adding a constant? 72. Graph on the same set of axes [latex]f\left(x\right)={x}^{2},f\left(x\right)={\left(x - 2\right)}^{2},f{\left(x - 3\right)}^{2},\text{ and }f\left(x\right)={\left(x+4\right)}^{2}\\[/latex]. What appears to be the effect of adding or subtracting those numbers? 73. The path of an object projected at a 45 degree angle with initial velocity of 80 feet per second is given by the function [latex]h\left(x\right)=\frac{-32}{{\left(80\right)}^{2}}{x}^{2}+x\\[/latex] where x is the horizontal distance traveled and [latex]h\left(x\right)\\[/latex] is the height in feet. Use the TRACE feature of your calculator to determine the height of the object when it has traveled 100 feet away horizontally. 74. A suspension bridge can be modeled by the quadratic function [latex]h\left(x\right)=.0001{x}^{2}\\[/latex] with [latex]-2000\le x\le 2000\\[/latex] where |x| is the number of feet from the center and [latex]h\left(x\right)\\[/latex] is height in feet. Use the TRACE feature of your calculator to estimate how far from the center does the bridge have a height of 100 feet. For the following exercises, use the vertex of the graph of the quadratic function and the direction the graph opens to find the domain and range of the function. 75. Vertex [latex]\left(1,-2\right)\\[/latex], opens up. 76. Vertex [latex]\left(-1,2\right)\\[/latex] opens down. 77. Vertex [latex]\left(-5,11\right)\\[/latex], opens down. 78. Vertex [latex]\left(-100,100\right)\\[/latex], opens up. For the following exercises, write the equation of the quadratic function that contains the given point and has the same shape as the given function. 79. Contains (1, 1) and has shape of [latex]f\left(x\right)=2{x}^{2}\\[/latex]. Vertex is on the y-axis. 80. Contains (-1, 4) and has the shape of [latex]f\left(x\right)=2{x}^{2}\\[/latex]. Vertex is on the y-axis. 81. Contains (2, 3) and has the shape of [latex]f\left(x\right)=3{x}^{2}\\[/latex]. Vertex is on the y-axis. 82. Contains (1, –3) and has the shape of [latex]f\left(x\right)=-{x}^{2}\\[/latex]. Vertex is on the y-axis. 83. Contains (4, 3) and has the shape of [latex]f\left(x\right)=5{x}^{2}\\[/latex]. Vertex is on the y-axis. 84. Contains (1, –6) has the shape of [latex]f\left(x\right)=3{x}^{2}\\[/latex]. Vertex has x-coordinate of –1. 85. Find the dimensions of the rectangular corral producing the greatest enclosed area given 200 feet of fencing. 86. Find the dimensions of the rectangular corral split into 2 pens of the same size producing the greatest possible enclosed area given 300 feet of fencing. 87. Find the dimensions of the rectangular corral producing the greatest enclosed area split into 3 pens of the same size given 500 feet of fencing. 88. Among all of the pairs of numbers whose sum is 6, find the pair with the largest product. What is the product? 89. Among all of the pairs of numbers whose difference is 12, find the pair with the smallest product. What is the product? 90. Suppose that the price per unit in dollars of a cell phone production is modeled by [latex]p=$45 - 0.0125x\\[/latex], where x is in thousands of phones produced, and the revenue represented by thousands of dollars is [latex]R=x\cdot p\\[/latex]. Find the production level that will maximize revenue. 91. A rocket is launched in the air. Its height, in meters above sea level, as a function of time, in seconds, is given by [latex]h\left(t\right)=-4.9{t}^{2}+229t+234\\[/latex]. Find the maximum height the rocket attains. 92. A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by [latex]h\left(t\right)=-4.9{t}^{2}+24t+8\\[/latex]. How long does it take to reach maximum height? 93. A soccer stadium holds 62,000 spectators. With a ticket price of $11, the average attendance has been 26,000. When the price dropped to $9, the average attendance rose to 31,000. Assuming that attendance is linearly related to ticket price, what ticket price would maximize revenue? 94. A farmer finds that if she plants 75 trees per acre, each tree will yield 20 bushels of fruit. She estimates that for each additional tree planted per acre, the yield of each tree will decrease by 3 bushels. How many trees should she plant per acre to maximize her harvest?

Licenses & Attributions

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..