Section Exercises
1. Explain the difference between the coefficient of a power function and its degree. 2. If a polynomial function is in factored form, what would be a good first step in order to determine the degree of the function? 3. In general, explain the end behavior of a power function with odd degree if the leading coefficient is positive. 4. What is the relationship between the degree of a polynomial function and the maximum number of turning points in its graph? 5. What can we conclude if, in general, the graph of a polynomial function exhibits the following end behavior? As [latex]x\to -\infty ,f\left(x\right)\to -\infty \\[/latex] and as [latex]x\to \infty ,f\left(x\right)\to -\infty \\[/latex]. For the following exercises, identify the function as a power function, a polynomial function, or neither. 6. [latex]f\left(x\right)={x}^{5}\\[/latex] 7. [latex]f\left(x\right)={\left({x}^{2}\right)}^{3}\\[/latex] 8. [latex]f\left(x\right)=x-{x}^{4}\\[/latex] 9. [latex]f\left(x\right)=\frac{{x}^{2}}{{x}^{2}-1}\\[/latex] 10. [latex]f\left(x\right)=2x\left(x+2\right){\left(x - 1\right)}^{2}\\[/latex] 11. [latex]f\left(x\right)={3}^{x+1}\\[/latex] For the following exercises, find the degree and leading coefficient for the given polynomial. 12. [latex]-3x{}^{4}\\[/latex] 13. [latex]7 - 2{x}^{2}\\[/latex] 14. [latex]-2{x}^{2}- 3{x}^{5}+ x - 6 \\[/latex] 15. [latex]x\left(4-{x}^{2}\right)\left(2x+1\right)\\[/latex] 16. [latex]{x}^{2}{\left(2x - 3\right)}^{2}\\[/latex] For the following exercises, determine the end behavior of the functions. 17. [latex]f\left(x\right)={x}^{4}\\[/latex] 18. [latex]f\left(x\right)={x}^{3}\\[/latex] 19. [latex]f\left(x\right)=-{x}^{4}\\[/latex] 20. [latex]f\left(x\right)=-{x}^{9}\\[/latex] 21. [latex]f\left(x\right)=-2{x}^{4}- 3{x}^{2}+ x - 1\\[/latex] 22. [latex]f\left(x\right)=3{x}^{2}+ x - 2\\[/latex] 23. [latex]f\left(x\right)={x}^{2}\left(2{x}^{3}-x+1\right)\\[/latex] 24. [latex]f\left(x\right)={\left(2-x\right)}^{7}\\[/latex] For the following exercises, find the intercepts of the functions. 25. [latex]f\left(t\right)=2\left(t - 1\right)\left(t+2\right)\left(t - 3\right)\\[/latex] 26. [latex]g\left(n\right)=-2\left(3n - 1\right)\left(2n+1\right)\\[/latex] 27. [latex]f\left(x\right)={x}^{4}-16\\[/latex] 28. [latex]f\left(x\right)={x}^{3}+27\\[/latex] 29. [latex]f\left(x\right)=x\left({x}^{2}-2x - 8\right)\\[/latex] 30. [latex]f\left(x\right)=\left(x+3\right)\left(4{x}^{2}-1\right)\\[/latex] For the following exercises, determine the least possible degree of the polynomial function shown. 31.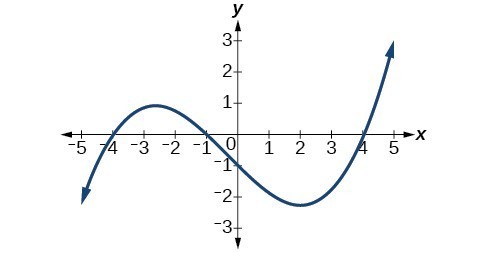 32.
32.
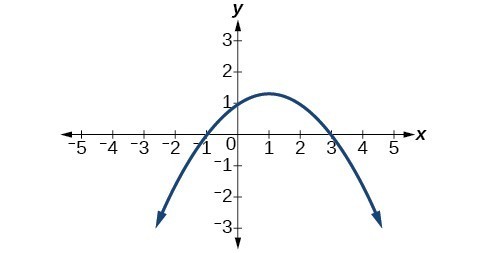 33.
33.
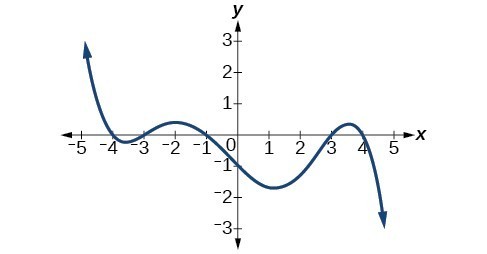 34.
34.
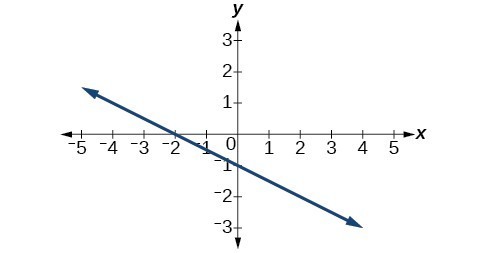 35.
35.
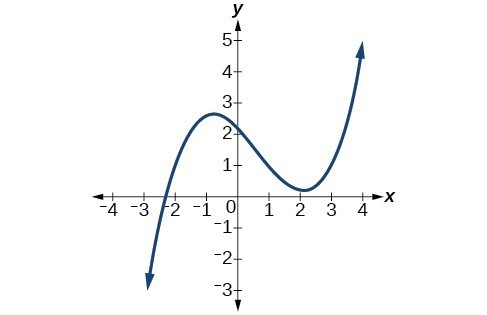 36.
36.
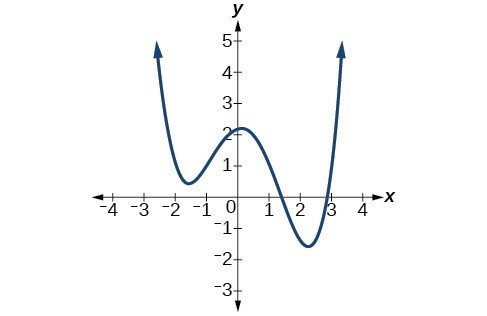 37.
37.
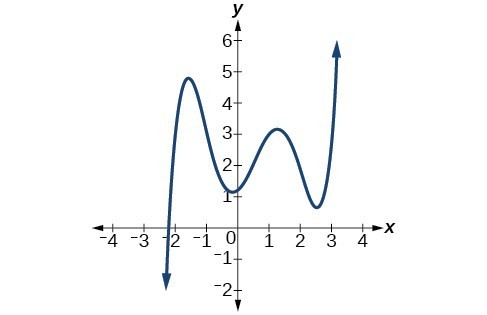 38.
38.
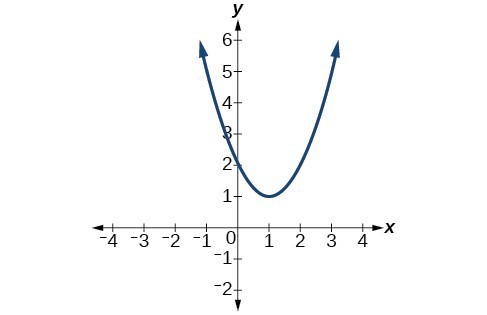 For the following exercises, determine whether the graph of the function provided is a graph of a polynomial function. If so, determine the number of turning points and the least possible degree for the function.
39.
For the following exercises, determine whether the graph of the function provided is a graph of a polynomial function. If so, determine the number of turning points and the least possible degree for the function.
39.
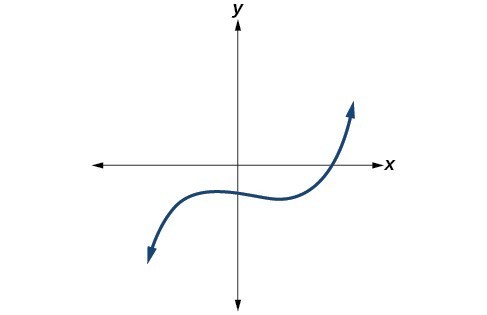 40.
40.
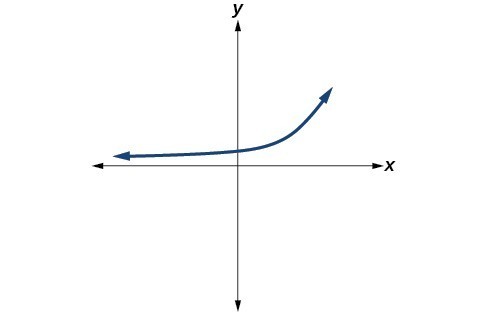 41.
41.
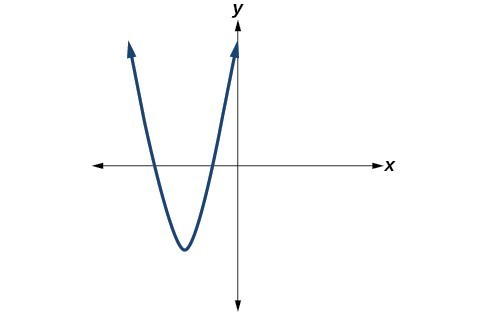 42.
42.
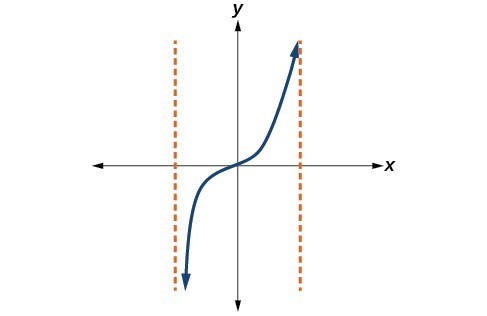 43.
43.
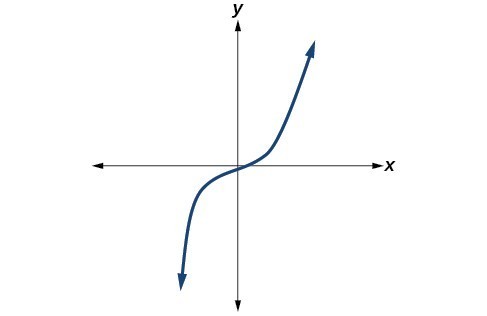 44.
44.
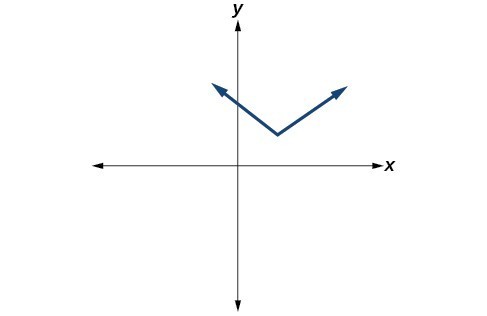 45.
45.
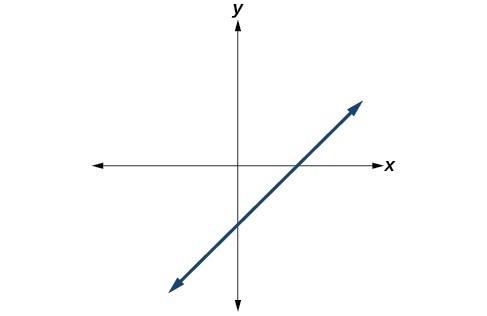 For the following exercises, make a table to confirm the end behavior of the function.
46. [latex]f\left(x\right)=-{x}^{3}\\[/latex]
47. [latex]f\left(x\right)={x}^{4}-5{x}^{2}\\[/latex]
48. [latex]f\left(x\right)={x}^{2}{\left(1-x\right)}^{2}\\[/latex]
49. [latex]f\left(x\right)=\left(x - 1\right)\left(x - 2\right)\left(3-x\right)\\[/latex]
50. [latex]f\left(x\right)=\frac{{x}^{5}}{10}-{x}^{4}\\[/latex]
For the following exercises, graph the polynomial functions using a calculator. Based on the graph, determine the intercepts and the end behavior.
51. [latex]f\left(x\right)={x}^{3}\left(x - 2\right)\\[/latex]
52. [latex]f\left(x\right)=x\left(x - 3\right)\left(x+3\right)\\[/latex]
53. [latex]f\left(x\right)=x\left(14 - 2x\right)\left(10 - 2x\right)\\[/latex]
54. [latex]f\left(x\right)=x\left(14 - 2x\right){\left(10 - 2x\right)}^{2}\\[/latex]
55. [latex]f\left(x\right)={x}^{3}-16x\\[/latex]
56. [latex]f\left(x\right)={x}^{3}-27\\[/latex]
57. [latex]f\left(x\right)={x}^{4}-81\\[/latex]
58. [latex]f\left(x\right)=-{x}^{3}+{x}^{2}+2x\\[/latex]
59. [latex]f\left(x\right)={x}^{3}-2{x}^{2}-15x\\[/latex]
60. [latex]f\left(x\right)={x}^{3}-0.01x\\[/latex]
For the following exercises, use the information about the graph of a polynomial function to determine the function. Assume the leading coefficient is 1 or –1. There may be more than one correct answer.
61. The y-intercept is [latex]\left(0,-4\right)\\[/latex]. The x-intercepts are [latex]\left(-2,0\right),\left(2,0\right)\\[/latex]. Degree is 2.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex].
62. The y-intercept is [latex]\left(0,9\right)\\[/latex]. The x-intercepts are [latex]\left(-3,0\right),\left(3,0\right)\\[/latex]. Degree is 2.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty\\ [/latex].
63. The y-intercept is [latex]\left(0,0\right)\\[/latex]. The x-intercepts are [latex]\left(0,0\right),\left(2,0\right)\\[/latex]. Degree is 3.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex].
64. The y-intercept is [latex]\left(0,1\right)\\[/latex]. The x-intercept is [latex]\left(1,0\right)\\[/latex]. Degree is 3.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty \\[/latex].
65. The y-intercept is [latex]\left(0,1\right)\\[/latex]. There is no x-intercept. Degree is 4.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty\\[/latex].
For the following exercises, use the written statements to construct a polynomial function that represents the required information.
66. An oil slick is expanding as a circle. The radius of the circle is increasing at the rate of 20 meters per day. Express the area of the circle as a function of d, the number of days elapsed.
67. A cube has an edge of 3 feet. The edge is increasing at the rate of 2 feet per minute. Express the volume of the cube as a function of m, the number of minutes elapsed.
68. A rectangle has a length of 10 inches and a width of 6 inches. If the length is increased by x inches and the width increased by twice that amount, express the area of the rectangle as a function of x.
69. An open box is to be constructed by cutting out square corners of x-inch sides from a piece of cardboard 8 inches by 8 inches and then folding up the sides. Express the volume of the box as a function of x.
70. A rectangle is twice as long as it is wide. Squares of side 2 feet are cut out from each corner. Then the sides are folded up to make an open box. Express the volume of the box as a function of the width (x).
For the following exercises, make a table to confirm the end behavior of the function.
46. [latex]f\left(x\right)=-{x}^{3}\\[/latex]
47. [latex]f\left(x\right)={x}^{4}-5{x}^{2}\\[/latex]
48. [latex]f\left(x\right)={x}^{2}{\left(1-x\right)}^{2}\\[/latex]
49. [latex]f\left(x\right)=\left(x - 1\right)\left(x - 2\right)\left(3-x\right)\\[/latex]
50. [latex]f\left(x\right)=\frac{{x}^{5}}{10}-{x}^{4}\\[/latex]
For the following exercises, graph the polynomial functions using a calculator. Based on the graph, determine the intercepts and the end behavior.
51. [latex]f\left(x\right)={x}^{3}\left(x - 2\right)\\[/latex]
52. [latex]f\left(x\right)=x\left(x - 3\right)\left(x+3\right)\\[/latex]
53. [latex]f\left(x\right)=x\left(14 - 2x\right)\left(10 - 2x\right)\\[/latex]
54. [latex]f\left(x\right)=x\left(14 - 2x\right){\left(10 - 2x\right)}^{2}\\[/latex]
55. [latex]f\left(x\right)={x}^{3}-16x\\[/latex]
56. [latex]f\left(x\right)={x}^{3}-27\\[/latex]
57. [latex]f\left(x\right)={x}^{4}-81\\[/latex]
58. [latex]f\left(x\right)=-{x}^{3}+{x}^{2}+2x\\[/latex]
59. [latex]f\left(x\right)={x}^{3}-2{x}^{2}-15x\\[/latex]
60. [latex]f\left(x\right)={x}^{3}-0.01x\\[/latex]
For the following exercises, use the information about the graph of a polynomial function to determine the function. Assume the leading coefficient is 1 or –1. There may be more than one correct answer.
61. The y-intercept is [latex]\left(0,-4\right)\\[/latex]. The x-intercepts are [latex]\left(-2,0\right),\left(2,0\right)\\[/latex]. Degree is 2.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex].
62. The y-intercept is [latex]\left(0,9\right)\\[/latex]. The x-intercepts are [latex]\left(-3,0\right),\left(3,0\right)\\[/latex]. Degree is 2.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty\\ [/latex].
63. The y-intercept is [latex]\left(0,0\right)\\[/latex]. The x-intercepts are [latex]\left(0,0\right),\left(2,0\right)\\[/latex]. Degree is 3.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex].
64. The y-intercept is [latex]\left(0,1\right)\\[/latex]. The x-intercept is [latex]\left(1,0\right)\\[/latex]. Degree is 3.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty \\[/latex].
65. The y-intercept is [latex]\left(0,1\right)\\[/latex]. There is no x-intercept. Degree is 4.
End behavior: [latex]\text{as }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty\\[/latex].
For the following exercises, use the written statements to construct a polynomial function that represents the required information.
66. An oil slick is expanding as a circle. The radius of the circle is increasing at the rate of 20 meters per day. Express the area of the circle as a function of d, the number of days elapsed.
67. A cube has an edge of 3 feet. The edge is increasing at the rate of 2 feet per minute. Express the volume of the cube as a function of m, the number of minutes elapsed.
68. A rectangle has a length of 10 inches and a width of 6 inches. If the length is increased by x inches and the width increased by twice that amount, express the area of the rectangle as a function of x.
69. An open box is to be constructed by cutting out square corners of x-inch sides from a piece of cardboard 8 inches by 8 inches and then folding up the sides. Express the volume of the box as a function of x.
70. A rectangle is twice as long as it is wide. Squares of side 2 feet are cut out from each corner. Then the sides are folded up to make an open box. Express the volume of the box as a function of the width (x).Licenses & Attributions
CC licensed content, Shared previously
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
