We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Section Exercises

1. Can the average rate of change of a function be constant? 2. If a function [latex]f[/latex] is increasing on [latex]\left(a,b\right)[/latex] and decreasing on [latex]\left(b,c\right)[/latex], then what can be said about the local extremum of [latex]f[/latex] on [latex]\left(a,c\right)?[/latex] 3. How are the absolute maximum and minimum similar to and different from the local extrema? 4. How does the graph of the absolute value function compare to the graph of the quadratic function, [latex]y={x}^{2}[/latex], in terms of increasing and decreasing intervals? For exercises 5–15, find the average rate of change of each function on the interval specified for real numbers [latex]b[/latex] or [latex]h[/latex]. 5. [latex]f\left(x\right)=4{x}^{2}-7[/latex] on [latex]\left[1,\text{ }b\right]\\[/latex] 6. [latex]g\left(x\right)=2{x}^{2}-9[/latex] on [latex]\left[4,\text{ }b\right]\\[/latex] 7. [latex]p\left(x\right)=3x+4[/latex] on [latex]\left[2,\text{ }2+h\right]\\[/latex] 8. [latex]k\left(x\right)=4x - 2[/latex] on [latex]\left[3,\text{ }3+h\right]\\[/latex] 9. [latex]f\left(x\right)=2{x}^{2}+1[/latex] on [latex]\left[x,x+h\right]\\[/latex] 10. [latex]g\left(x\right)=3{x}^{2}-2[/latex] on [latex]\left[x,x+h\right]\\[/latex] 11. [latex]a\left(t\right)=\frac{1}{t+4}[/latex] on [latex]\left[9,9+h\right]\\[/latex] 12. [latex]b\left(x\right)=\frac{1}{x+3}[/latex] on [latex]\left[1,1+h\right]\\[/latex] 13. [latex]j\left(x\right)=3{x}^{3}[/latex] on [latex]\left[1,1+h\right]\\[/latex] 14. [latex]r\left(t\right)=4{t}^{3}[/latex] on [latex]\left[2,2+h\right]\\[/latex] 15. [latex]\frac{f\left(x+h\right)-f\left(x\right)}{h}\\[/latex] given [latex]f\left(x\right)=2{x}^{2}-3x\\[/latex] on [latex]\left[x,x+h\right]\\[/latex] For exercises 16–17, consider the graph of [latex]f[/latex].Graph of a polynomial. As y increases, the line increases to x = 5, decreases to x =3, increases to x = 7, decreases to x = 3, and then increases infinitely. 16. Estimate the average rate of change from [latex]x=1[/latex] to [latex]x=4[/latex]. 17. Estimate the average rate of change from [latex]x=2[/latex] to [latex]x=5[/latex]. For exercises 18–21, use the graph of each function to estimate the intervals on which the function is increasing or decreasing. 18. Graph of an absolute value function with minimum at (1, -3), and f(x) approaching positive infinity as x approaches negative infinity, f(x) approaches positive infinity as x approaches infinity. 19. 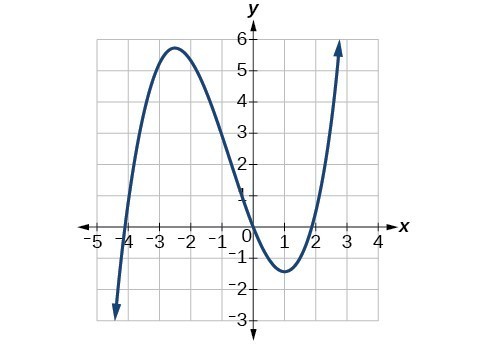Graph of a cubic function with f(x) decreasing to negative infinity as x approaches negative infinity, a local maximum at (-2.5, 5.5), passing through the origin, a local min. at (-1.5, 1) and f(x) increasing to positive infinity as x approaches positive infinity. 20. Graph of a cubic function with f(x) increasing to positive infinity as x approaches negative infinity, a local minimum at (-1.5, -2.5), passing through the origin, a local max. at (2, 4.5) and f(x) decreasing to negative infinity as x approaches positive infinity. 21. Graph of a reciprocal function with an asymptote between 2 and 3, f(x) decreases to negative infinity as x approaches negative infinity, f(x) has a local max at (1,0), and approaches negative infinity as x approaches 3 from the left. f(x) approaches negative infinity as x approaches positive infinity, with f(x) approaching negative infinity as x approaches 3 from the right side. For exercises 22–23, consider the graph shown below. Graph of a cubic function passing through the origin, with local max at approximately (-3, 50) and decreasing to negative infinity as x approaches negative infinity. f(x) has a local minimum at (3, -50) and approaches infinity as x approaches positive infinity. 22. Estimate the intervals where the function is increasing or decreasing. 23. Estimate the point(s) at which the graph of [latex]f[/latex] has a local maximum or a local minimum. For exercises 24–25, consider the graph below. Graph of a cubic function. 24. If the complete graph of the function is shown, estimate the intervals where the function is increasing or decreasing. 25. If the complete graph of the function is shown, estimate the absolute maximum and absolute minimum. 26. The table below gives the annual sales (in millions of dollars) of a product from 1998 to 2006. What was the average rate of change of annual sales (a) between 2001 and 2002, and (b) between 2001 and 2004?
Year Sales (millions of dollars)
1998 201
1999 219
2000 233
2001 243
2002 249
2003 251
2004 249
2005 243
2006 233
27. The table below gives the population of a town (in thousands) from 2000 to 2008. What was the average rate of change of population (a) between 2002 and 2004, and (b) between 2002 and 2006?
Year Population (thousands)
2000 87
2001 84
2002 83
2003 80
2004 77
2005 76
2006 78
2007 81
2008 85
For the following exercises, find the average rate of change of each function on the interval specified. 28. [latex]f\left(x\right)={x}^{2}[/latex] on [latex]\left[1,\text{ }5\right]\\[/latex] 29. [latex]h\left(x\right)=5 - 2{x}^{2}[/latex] on [latex]\left[-2,\text{4}\right]\\[/latex] 30. [latex]q\left(x\right)={x}^{3}[/latex] on [latex]\left[-4,\text{2}\right]\\[/latex] 31. [latex]g\left(x\right)=3{x}^{3}-1[/latex] on [latex]\left[-3,\text{3}\right]\\[/latex] 32. [latex]y=\frac{1}{x}[/latex] on [latex]\left[1,\text{ 3}\right]\\[/latex] 33. [latex]p\left(t\right)=\frac{\left({t}^{2}-4\right)\left(t+1\right)}{{t}^{2}+3}\\[/latex] on [latex]\left[-3,\text{1}\right]\\[/latex] 34. [latex]k\left(t\right)=6{t}^{2}+\frac{4}{{t}^{3}}\\[/latex] on [latex]\left[-1,3\right]\\[/latex] For the following exercises, use a graphing utility to estimate the local extrema of each function and to estimate the intervals on which the function is increasing and decreasing. 35. [latex]f\left(x\right)={x}^{4}-4{x}^{3}+5\\[/latex] 36. [latex]h\left(x\right)={x}^{5}+5{x}^{4}+10{x}^{3}+10{x}^{2}-1\\[/latex] 37. [latex]g\left(t\right)=t\sqrt{t+3}\\[/latex] 38. [latex]k\left(t\right)=3{t}^{\frac{2}{3}}-t\\[/latex] 39. [latex]m\left(x\right)={x}^{4}+2{x}^{3}-12{x}^{2}-10x+4\\[/latex] 40. [latex]n\left(x\right)={x}^{4}-8{x}^{3}+18{x}^{2}-6x+2\\[/latex] 41.The graph of the function [latex]f[/latex] is shown below. Graph of f(x) on a graphing calculator. Based on the calculator screenshot, the point [latex]\left(1.333,\text{ }5.185\right)\\[/latex] is which of the following? A) a relative (local) maximum of the function B) the vertex of the function C) the absolute maximum of the function D) a zero of the function. 42. Let [latex]f\left(x\right)=\frac{1}{x}\\[/latex]. Find a number [latex]c[/latex] such that the average rate of change of the function [latex]f[/latex] on the interval [latex]\left(1,c\right)\\[/latex] is [latex]-\frac{1}{4}\\[/latex]. 43. Let [latex]f\left(x\right)=\frac{1}{x}[/latex] . Find the number [latex]b[/latex] such that the average rate of change of [latex]f[/latex] on the interval [latex]\left(2,b\right)\\[/latex] is [latex]-\frac{1}{10}\\[/latex]. 44. At the start of a trip, the odometer on a car read 21,395. At the end of the trip, 13.5 hours later, the odometer read 22,125. Assume the scale on the odometer is in miles. What is the average speed the car traveled during this trip? 45. A driver of a car stopped at a gas station to fill up his gas tank. He looked at his watch, and the time read exactly 3:40 p.m. At this time, he started pumping gas into the tank. At exactly 3:44, the tank was full and he noticed that he had pumped 10.7 gallons. What is the average rate of flow of the gasoline into the gas tank? 46. Near the surface of the moon, the distance that an object falls is a function of time. It is given by [latex]d\left(t\right)=2.6667{t}^{2}\\[/latex], where [latex]t[/latex] is in seconds and [latex]d\left(t\right)[/latex] is in feet. If an object is dropped from a certain height, find the average velocity of the object from [latex]t=1[/latex] to [latex]t=2[/latex]. 47. The graph below illustrates the decay of a radioactive substance over [latex]t[/latex] days. Graph of an exponential function. Use the graph to estimate the average decay rate from [latex]t=5[/latex] to [latex]t=15[/latex].

Licenses & Attributions

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..