We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > College Algebra

Solutions

Solutions to Try Its

1. [latex]f\left(x\right)\\[/latex] is a power function because it can be written as [latex]f\left(x\right)=8{x}^{5}\\[/latex]. The other functions are not power functions. 2. As x approaches positive or negative infinity, [latex]f\left(x\right)\\[/latex] decreases without bound: as [latex]x\to \pm \infty , f\left(x\right)\to -\infty\\ [/latex] because of the negative coefficient. 3. The degree is 6. The leading term is [latex]-{x}^{6}\\[/latex]. The leading coefficient is –1. 4. As [latex]x\to \infty , f\left(x\right)\to -\infty ; as x\to -\infty , f\left(x\right)\to -\infty \\[/latex]. It has the shape of an even degree power function with a negative coefficient. 5. The leading term is [latex]0.2{x}^{3}\\[/latex], so it is a degree 3 polynomial. As x approaches positive infinity, [latex]f\left(x\right)\\[/latex] increases without bound; as x approaches negative infinity, [latex]f\left(x\right)\\[/latex] decreases without bound. 6. y-intercept [latex]\left(0,0\right)\\[/latex]; x-intercepts [latex]\left(0,0\right),\left(-2,0\right)\\[/latex], and [latex]\left(5,0\right)\\[/latex] 7. There are at most 12 x-intercepts and at most 11 turning points. 8. The end behavior indicates an odd-degree polynomial function; there are 3 x-intercepts and 2 turning points, so the degree is odd and at least 3. Because of the end behavior, we know that the lead coefficient must be negative. 9. The x-intercepts are [latex]\left(2,0\right),\left(-1,0\right)\\[/latex], and [latex]\left(5,0\right)\\[/latex], the y-intercept is [latex]\left(0,\text{2}\right)\\[/latex], and the graph has at most 2 turning points.

Solutions to Odd-Numbered Exercises

1. The coefficient of the power function is the real number that is multiplied by the variable raised to a power. The degree is the highest power appearing in the function. 3. As x decreases without bound, so does [latex]f\left(x\right)\\[/latex]. As x increases without bound, so does [latex]f\left(x\right)\\[/latex]. 5. The polynomial function is of even degree and leading coefficient is negative. 7. Power function 9. Neither 11. Neither 13. Degree = 2, Coefficient = –2 15. Degree =4, Coefficient = –2 17. [latex]\text{As }x\to \infty ,f\left(x\right)\to \infty ,\text{ as }x\to -\infty ,f\left(x\right)\to \infty \\[/latex] 19. [latex]\text{As }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty \\[/latex] 21. [latex]\text{As }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty \\[/latex] 23. [latex]\text{As }x\to \infty ,f\left(x\right)\to \infty ,\text{ as }x\to -\infty ,f\left(x\right)\to -\infty \\[/latex] 25. y-intercept is [latex]\left(0,12\right)\\[/latex], t-intercepts are [latex]\left(1,0\right);\left(-2,0\right);\text{and }\left(3,0\right)\\[/latex]. 27. y-intercept is [latex]\left(0,-16\right)\\[/latex]. x-intercepts are [latex]\left(2,0\right)\\[/latex] and [latex]\left(-2,0\right)\\[/latex]. 29. y-intercept is [latex]\left(0,0\right)\\[/latex].i x-intercepts are [latex]\left(0,0\right),\left(4,0\right)\\[/latex], and [latex]\left(-2, 0\right)\\[/latex]. 31. 3 33. 5 35. 3 37. 5 39. Yes. Number of turning points is 2. Least possible degree is 3. 41. Yes. Number of turning points is 1. Least possible degree is 2. 43. Yes. Number of turning points is 0. Least possible degree is 1. 45. Yes. Number of turning points is 0. Least possible degree is 1. 47. [latex]\text{As }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex]
x f(x)
10 9,500
100 99,950,000
–10 9,500
–100 99,950,000
49. [latex]\text{As }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty \\[/latex]
x f(x)
10 –504
100 –941,094
–10 1,716
–100 1,061,106
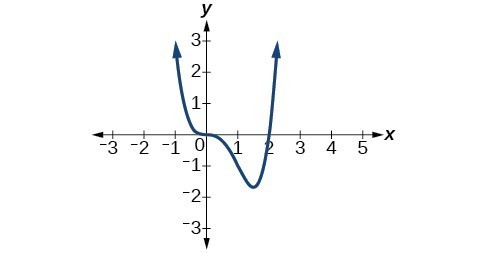51. The y-intercept is [latex]\left(0, 0\right)\\[/latex]. The x-intercepts are [latex]\left(0, 0\right),\text{ }\left(2, 0\right)\\[/latex]. [latex]\text{As }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex] Graph of f(x)=x^3(x-2). 53. The y-intercept is [latex]\left(0,0\right)\\[/latex]. The x-intercepts are [latex]\left(0, 0\right),\text{ }\left(5, 0\right),\text{ }\left(7, 0\right)\\[/latex]. [latex]\text{As }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex] 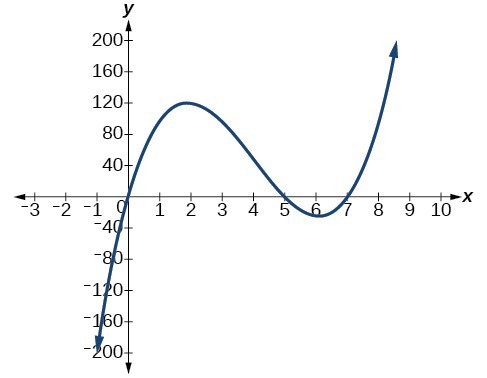Graph of f(x)=x(14-2x)(10-2x). 55. The y-intercept is [latex]\left(0, 0\right)\\[/latex]. The x-intercept is [latex]\left(-4, 0\right),\text{ }\left(0, 0\right),\text{ }\left(4, 0\right)\\[/latex]. [latex]\text{As }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex] 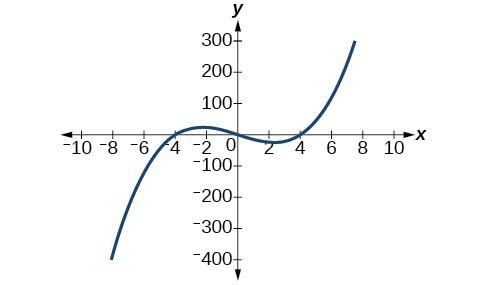57. The y-intercept is [latex]\left(0, -81\right)[/latex]. The x-intercept are [latex]\left(3, 0\right),\text{ }\left(-3, 0\right)\\[/latex]. [latex]\text{As }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex] 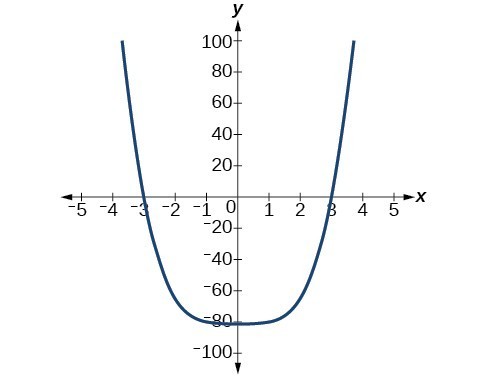Graph of f(x)=x^3-27. 59. The y-intercept is [latex]\left(0, 0\right)\\[/latex]. The x-intercepts are [latex]\left(-3, 0\right),\text{ }\left(0, 0\right),\text{ }\left(5, 0\right)\\[/latex]. [latex]\text{As }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty \\[/latex] Graph of f(x)=-x^3+x^2+2x. 61. [latex]f\left(x\right)={x}^{2}-4\\[/latex] 63. [latex]f\left(x\right)={x}^{3}-4{x}^{2}+4x\\[/latex] 65. [latex]f\left(x\right)={x}^{4}+1\\[/latex] 67. [latex]V\left(m\right)=8{m}^{3}+36{m}^{2}+54m+27\\[/latex] 69. [latex]V\left(x\right)=4{x}^{3}-32{x}^{2}+64x\\[/latex]

Licenses & Attributions

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..