Identifying Nondegenerate Conics in General Form
In previous sections of this chapter, we have focused on the standard form equations for nondegenerate conic sections. In this section, we will shift our focus to the general form equation, which can be used for any conic. The general form is set equal to zero, and the terms and coefficients are given in a particular order, as shown below.
[latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0[/latex]
where [latex]A,B[/latex], and [latex]C[/latex] are not all zero. We can use the values of the coefficients to identify which type conic is represented by a given equation.
You may notice that the general form equation has an [latex]xy[/latex] term that we have not seen in any of the standard form equations. As we will discuss later, the [latex]xy[/latex] term rotates the conic whenever [latex]\text{ }B\text{ }[/latex] is not equal to zero.
| Conic Sections | Example |
|---|---|
| ellipse | [latex]4{x}^{2}+9{y}^{2}=1[/latex] |
| circle | [latex]4{x}^{2}+4{y}^{2}=1[/latex] |
| hyperbola | [latex]4{x}^{2}-9{y}^{2}=1[/latex] |
| parabola | [latex]4{x}^{2}=9y\text{ or }4{y}^{2}=9x[/latex] |
| one line | [latex]4x+9y=1[/latex] |
| intersecting lines | [latex]\left(x - 4\right)\left(y+4\right)=0[/latex] |
| parallel lines | [latex]\left(x - 4\right)\left(x - 9\right)=0[/latex] |
| a point | [latex]4{x}^{2}+4{y}^{2}=0[/latex] |
| no graph | [latex]4{x}^{2}+4{y}^{2}=-1[/latex] |
A General Note: General Form of Conic Sections
A nondegenerate conic section has the general form[latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0[/latex]
where [latex]A,B[/latex], and [latex]C[/latex] are not all zero.
The table below summarizes the different conic sections where [latex]B=0[/latex], and [latex]A[/latex] and [latex]C[/latex] are nonzero real numbers. This indicates that the conic has not been rotated.
| ellipse | [latex]A{x}^{2}+C{y}^{2}+Dx+Ey+F=0,\text{ }A\ne C\text{ and }AC>0[/latex] |
| circle | [latex]A{x}^{2}+C{y}^{2}+Dx+Ey+F=0,\text{ }A=C[/latex] |
| hyperbola | [latex]A{x}^{2}-C{y}^{2}+Dx+Ey+F=0\text{ or }-A{x}^{2}+C{y}^{2}+Dx+Ey+F=0[/latex], where [latex]A[/latex] and [latex]C[/latex] are positive |
| parabola | [latex]A{x}^{2}+Dx+Ey+F=0\text{ or }C{y}^{2}+Dx+Ey+F=0[/latex] |
How To: Given the equation of a conic, identify the type of conic.
- Rewrite the equation in the general form, [latex]A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0[/latex].
- Identify the values of [latex]A[/latex] and [latex]C[/latex] from the general form.
- If [latex]A[/latex] and [latex]C[/latex] are nonzero, have the same sign, and are not equal to each other, then the graph is an ellipse.
- If [latex]A[/latex] and [latex]C[/latex] are equal and nonzero and have the same sign, then the graph is a circle.
- If [latex]A[/latex] and [latex]C[/latex] are nonzero and have opposite signs, then the graph is a hyperbola.
- If either [latex]A[/latex] or [latex]C[/latex] is zero, then the graph is a parabola.
Example 1: Identifying a Conic from Its General Form
Identify the graph of each of the following nondegenerate conic sections.- [latex]4{x}^{2}-9{y}^{2}+36x+36y - 125=0[/latex]
- [latex]9{y}^{2}+16x+36y - 10=0[/latex]
- [latex]3{x}^{2}+3{y}^{2}-2x - 6y - 4=0[/latex]
- [latex]-25{x}^{2}-4{y}^{2}+100x+16y+20=0[/latex]
Solution
- Rewriting the general form, we have
 [latex]A=4[/latex] and [latex]C=-9[/latex], so we observe that [latex]A[/latex] and [latex]C[/latex] have opposite signs. The graph of this equation is a hyperbola.
[latex]A=4[/latex] and [latex]C=-9[/latex], so we observe that [latex]A[/latex] and [latex]C[/latex] have opposite signs. The graph of this equation is a hyperbola. - Rewriting the general form, we have
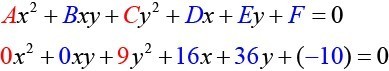 [latex]A=0[/latex] and [latex]C=9[/latex]. We can determine that the equation is a parabola, since [latex]A[/latex] is zero.
[latex]A=0[/latex] and [latex]C=9[/latex]. We can determine that the equation is a parabola, since [latex]A[/latex] is zero. - Rewriting the general form, we have
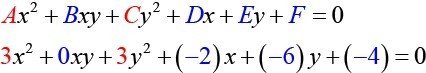 [latex]A=3[/latex] and [latex]C=3[/latex]. Because [latex]A=C[/latex], the graph of this equation is a circle.
[latex]A=3[/latex] and [latex]C=3[/latex]. Because [latex]A=C[/latex], the graph of this equation is a circle. - Rewriting the general form, we have
 [latex]A=-25[/latex] and [latex]C=-4[/latex]. Because [latex]AC>0[/latex] and [latex]A\ne C[/latex], the graph of this equation is an ellipse.
[latex]A=-25[/latex] and [latex]C=-4[/latex]. Because [latex]AC>0[/latex] and [latex]A\ne C[/latex], the graph of this equation is an ellipse.
Try It 1
Identify the graph of each of the following nondegenerate conic sections.- [latex]16{y}^{2}-{x}^{2}+x - 4y - 9=0[/latex]
- [latex]16{x}^{2}+4{y}^{2}+16x+49y - 81=0[/latex]
Licenses & Attributions
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
