We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Read: Imaginary and Complex Numbers

Learning Objectives

  • Express roots of negative numbers in terms of i.
  • Express imaginary numbers as bi and complex numbers as [latex]a+bi[/latex].
You really need only one new number to start working with the square roots of negative numbers. That number is the square root of [latex]−1,\sqrt{-1}[/latex]. The real numbers are those that can be shown on a number line—they seem pretty real to us! When something’s not real, you often say it is imaginary. So let’s call this new number i and use it to represent the square root of [latex]−1[/latex].

[latex] i=\sqrt{-1}[/latex]

Because [latex] \sqrt{x}\,\cdot \,\sqrt{x}=x[/latex], we can also see that [latex] \sqrt{-1}\,\cdot \,\sqrt{-1}=-1[/latex] or [latex] i\,\cdot \,i=-1[/latex]. We also know that [latex] i\,\cdot \,i={{i}^{2}}[/latex], so we can conclude that [latex] {{i}^{2}}=-1[/latex].

[latex] {{i}^{2}}=-1[/latex]

The number i allows us to work with roots of all negative numbers, not just [latex] \sqrt{-1}[/latex]. There are two important rules to remember: [latex] \sqrt{-1}=i[/latex], and [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex]. You will use these rules to rewrite the square root of a negative number as the square root of a positive number times [latex] \sqrt{-1}[/latex]. Next you will simplify the square root and rewrite [latex] \sqrt{-1}[/latex] as i. Let’s try an example.

Example

Simplify. [latex] \sqrt{-4}[/latex]

Answer: Use the rule [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex] \sqrt{-1}[/latex]. [latex-display] \sqrt{-4}=\sqrt{4\cdot -1}=\sqrt{4}\sqrt{-1}[/latex-display] Since [latex]4[/latex] is a perfect square [latex](4=2^{2})[/latex], you can simplify the square root of [latex]4[/latex]. [latex-display] \sqrt{4}\sqrt{-1}=2\sqrt{-1}[/latex-display] Use the definition of i to rewrite [latex] \sqrt{-1}[/latex] as i. [latex-display] 2\sqrt{-1}=2i[/latex-display]

Answer

[latex-display] \sqrt{-4}=2i[/latex-display]

Example

Simplify. [latex] \sqrt{-18}[/latex]

Answer: Use the rule [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex] \sqrt{-1}[/latex]. [latex-display] \sqrt{-18}=\sqrt{18\cdot -1}=\sqrt{18}\sqrt{-1}[/latex-display] Since [latex]18[/latex] is not a perfect square, use the same rule to rewrite it using factors that are perfect squares. In this case, [latex]9[/latex] is the only perfect square factor, and the square root of [latex]9[/latex] is [latex]3[/latex]. [latex-display] \sqrt{18}\sqrt{-1}=\sqrt{9}\sqrt{2}\sqrt{-1}=3\sqrt{2}\sqrt{-1}[/latex-display] Use the definition of i to rewrite [latex] \sqrt{-1}[/latex] as i. [latex-display] 3\sqrt{2}\sqrt{-1}=3\sqrt{2}i=3i\sqrt{2}[/latex-display] Remember to write i in front of the radical.

Answer

[latex-display] \sqrt{-18}=3i\sqrt[{}]{2}[/latex-display]

Example

Simplify. [latex] -\sqrt{-72}[/latex]

Answer: Use the rule [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex] to rewrite this as a product using [latex] \sqrt{-1}[/latex]. [latex-display] -\sqrt{-72}=-\sqrt{72\cdot -1}=-\sqrt{72}\sqrt{-1}[/latex-display] Since [latex]72[/latex] is not a perfect square, use the same rule to rewrite it using factors that are perfect squares. Notice that [latex]72[/latex] has three perfect squares as factors: [latex]4, 9[/latex], and [latex]36[/latex]. It’s easiest to use the largest factor that is a perfect square. [latex-display] -\sqrt{72}\sqrt{-1}=-\sqrt{36}\sqrt{2}\sqrt{-1}=-6\sqrt{2}\sqrt{-1}[/latex-display] Use the definition of i to rewrite [latex] \sqrt{-1}[/latex] as i. [latex-display] -6\sqrt{2}\sqrt{-1}=-6\sqrt{2}i=-6i\sqrt{2}[/latex-display] Remember to write i in front of the radical.

Answer

[latex-display] -\sqrt{-72}=-6i\sqrt[{}]{2}[/latex-display]

You may have wanted to simplify [latex] -\sqrt{-72}[/latex] using different factors. Some may have thought of rewriting this radical as [latex] -\sqrt{-9}\sqrt{8}[/latex], or [latex] -\sqrt{-4}\sqrt{18}[/latex], or [latex] -\sqrt{-6}\sqrt{12}[/latex] for instance. Each of these radicals would have eventually yielded the same answer of [latex] -6i\sqrt{2}[/latex]. In the following video, we show more examples of how to use imaginary numbers to simplify a square root with a negative radicand. https://youtu.be/LSp7yNP6Xxc

Rewriting the Square Root of a Negative Number

  • Find perfect squares within the radical.
  • Rewrite the radical using the rule [latex] \sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex].
  • Rewrite [latex] \sqrt{-1}[/latex] as i.
Example: [latex] \sqrt{-18}=\sqrt{9}\sqrt{-2}=\sqrt{9}\sqrt{2}\sqrt{-1}=3i\sqrt{2}[/latex]

Complex Numbers

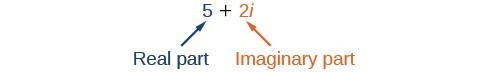
Showing the real and imaginary parts of 5 + 2i. In this complex number, 5 is the real part and 2i is the complex part.

A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written a + bi where a is the real part and bi is the imaginary part. For example, [latex]5+2i[/latex] is a complex number. So, too, is [latex]3+4\sqrt{3}i[/latex].

Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.

You can use the usual operations (addition, subtraction, multiplication, and so on) with imaginary numbers. You’ll see more of that, later. When you add a real number to an imaginary number, however, you get a complex number. A complex number is any number in the form [latex]a+bi[/latex], where a is a real number and bi is an imaginary number. The number a is sometimes called the real part of the complex number, and bi is sometimes called the imaginary part.
Complex Number Real part Imaginary part
[latex]3+7i[/latex] [latex]3[/latex] [latex]7i[/latex]
[latex]18–32i[/latex] [latex]18[/latex] [latex]−32i[/latex]
[latex] -\frac{3}{5}+i\sqrt{2}[/latex] [latex] -\frac{3}{5}[/latex] [latex] i\sqrt{2}[/latex]
[latex] \frac{\sqrt{2}}{2}-\frac{1}{2}i[/latex] [latex] \frac{\sqrt{2}}{2}[/latex] [latex]-\frac{1}{2}i[/latex]
In a number with a radical as part of b, such as [latex]-\frac{3}{5}+i\sqrt{2}[/latex] above, the imaginary i should be written in front of the radical. Though writing this number as [latex] -\frac{3}{5}+\sqrt{2}i[/latex] is technically correct, it makes it much more difficult to tell whether i is inside or outside of the radical. Putting it before the radical, as in [latex] -\frac{3}{5}+i\sqrt{2}[/latex], clears up any confusion. Look at these last two examples.
Number Number in complex form: [latex]a+bi[/latex] Real part Imaginary part
[latex]17[/latex] [latex]17+0i[/latex] [latex]17[/latex] [latex]0i[/latex]
[latex]−3i[/latex] [latex]0–3i[/latex] [latex]0[/latex] [latex]−3i[/latex]
By making [latex]b=0[/latex], any real number can be expressed as a complex number. The real number a is written [latex]a+0i[/latex] in complex form. Similarly, any imaginary number can be expressed as a complex number. By making [latex]a=0[/latex], any imaginary number [latex]bi[/latex] is written [latex]0+bi[/latex] in complex form.

Example

Write [latex]83.6[/latex] as a complex number.

Answer: Remember that a complex number has the form [latex]a+bi[/latex]. You need to figure out what a and b need to be. [latex-display]a+bi[/latex-display] Since [latex]83.6[/latex] is a real number, it is the real part (a) of the complex number [latex]a+bi[/latex]. A real number does not contain any imaginary parts, so the value of [latex]b[/latex] is [latex]0[/latex]. [latex-display]83.6+bi[/latex-display]

Answer

[latex-display]83.6+0i[/latex-display]

Example

Write [latex]−3i[/latex] as a complex number.

Answer: Remember that a complex number has the form [latex]a+bi[/latex]. You need to figure out what a and b need to be. [latex-display]a+bi[/latex-display] Since [latex]−3i[/latex] is an imaginary number, it is the imaginary part [latex]bi[/latex] of the complex number [latex]a+bi[/latex]. This imaginary number has no real parts, so the value of [latex]a[/latex] is [latex]0[/latex]. [latex-display]a–3i[/latex-display]

Answer

[latex-display]0–3i[/latex-display]

In the next video we show more examples of how to write numbers as complex numbers. https://youtu.be/mfoOYdDkuyY

Summary

Complex numbers have the form [latex]a+bi[/latex], where a and b are real numbers and i is the square root of [latex]−1[/latex]. All real numbers can be written as complex numbers by setting [latex]b=0[/latex]. Imaginary numbers have the form bi and can also be written as complex numbers by setting [latex]a=0[/latex]. Square roots of negative numbers can be simplified using [latex] \sqrt{-1}=i[/latex] and [latex] \sqrt{ab}=\sqrt{a}\sqrt{b}[/latex].

Licenses & Attributions

CC licensed content, Original

  • Write Number in the Form of Complex Numbers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Simplify Square Roots to Imaginary Numbers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.