We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Read: Composite and Inverse Functions

Learning Objectives

  • Define a composite function
  • Define an inverse function
  • Use compositions of functions to verify inverses algebraically
  • Identify an inverse algebraically
  • Identify the domain and range of inverse functions with tables

Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. Notice how we have just defined two relationships: The cost depends on the temperature, and the temperature depends on the day.

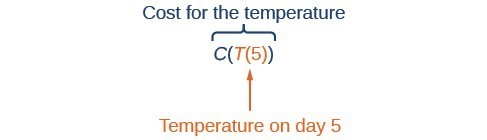Explanation of C(T(5)), which is the cost for the temperature and T(5) is the temperature on day 5. Figure 1

Using descriptive variables, we can notate these two functions. The function [latex]C\left(T\right)[/latex] gives the cost [latex]C[/latex] of heating a house for a given average daily temperature in [latex]T[/latex] degrees Celsius. The function [latex]T\left(d\right)[/latex] gives the average daily temperature on day [latex]d[/latex] of the year. For any given day, [latex]\text{Cost}=C\left(T\left(d\right)\right)[/latex] means that the cost depends on the temperature, which in turns depends on the day of the year. Thus, we can evaluate the cost function at the temperature [latex]T\left(d\right)[/latex]. For example, we could evaluate [latex]T\left(5\right)[/latex] to determine the average daily temperature on the [latex]5[/latex]th day of the year. Then, we could evaluate the cost function at that temperature. We would write [latex]C\left(T\left(5\right)\right)[/latex]. By combining these two relationships into one function, we have performed function composition.

We read the left-hand side as [latex]"f[/latex] composed with [latex]g[/latex] at [latex]x,"[/latex] and the right-hand side as [latex]"f[/latex] of [latex]g[/latex] of [latex]x."[/latex] The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol [latex]\circ [/latex] is called the composition operator. It is also important to understand the order of operations in evaluating a composite function. We follow the usual convention with parentheses by starting with the innermost parentheses first, and then working to the outside.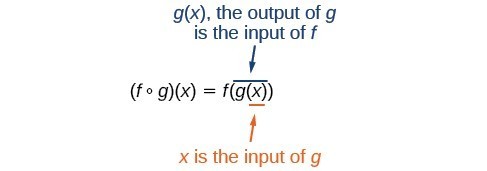   Explanation of the composite function. g(x), the output of g is the input of f. X is the input of g.

Example

Using the functions provided, find [latex]f\left(g\left(x\right)\right)[/latex] and [latex]g\left(f\left(x\right)\right)[/latex]. [latex-display]f\left(x\right)=2x+1[/latex-display] [latex-display]g\left(x\right)=3-x[/latex-display]

Answer: [latex-display]f\left(x\right)=2x+1[/latex-display] [latex-display]g\left(x\right)=3-x[/latex-display] Let’s begin by substituting [latex]g\left(x\right)[/latex] into [latex]f\left(x\right)[/latex].[latex]\begin{array}f\left(g\left(x\right)\right)=2\left(3-x\right)+1\hfill \\ \text{ }=6 - 2x+1\hfill \\ \text{ }=7 - 2x\hfill \end{array}[/latex] Now we can substitute [latex]f\left(x\right)[/latex] into [latex]g\left(x\right)[/latex].

[latex]\begin{array}g\left(f\left(x\right)\right)=3-\left(2x+1\right)\hfill \\ \text{ }=3 - 2x - 1\hfill \\ \text{ }=-2x+2\hfill \end{array}[/latex]

In the following video you will see another example of how to find the composition of two functions. https://youtu.be/r_LssVS4NHk

Inverse Functions

An inverse function is a function for which the input of the original function becomes the output of the inverse function. This naturally leads to the output of the original function becoming the input of the inverse function. The reason we want to introduce inverse functions is because exponential and logarithmic functions are inverses of each other, and understanding this quality helps to make understanding logarithmic functions easier. And the reason we introduced composite functions is because you can verify, algebraically, whether two functions are inverses of each other by using a composition.

Given a function [latex]f\left(x\right)[/latex], we represent its inverse as [latex]{f}^{-1}\left(x\right)[/latex], read as [latex]"f[/latex] inverse of [latex]x.\text{"}[/latex] The raised [latex]-1[/latex] is part of the notation. It is not an exponent; it does not imply a power of [latex]-1[/latex] . In other words, [latex]{f}^{-1}\left(x\right)[/latex] does not mean [latex]\frac{1}{f\left(x\right)}[/latex] because [latex]\frac{1}{f\left(x\right)}[/latex] is the reciprocal of [latex]f[/latex] and not the inverse.

Just as zero does not have a reciprocal, some functions do not have inverses.

Inverse Function

For any one-to-one function [latex]f\left(x\right)=y[/latex], a function [latex]{f}^{-1}\left(x\right)[/latex] is an inverse function of [latex]f[/latex] if [latex]{f}^{-1}\left(y\right)=x[/latex].

The notation [latex]{f}^{-1}[/latex] is read [latex]\text{"}f[/latex] inverse." Like any other function, we can use any variable name as the input for [latex]{f}^{-1}[/latex], so we will often write [latex]{f}^{-1}\left(x\right)[/latex], which we read as [latex]"f[/latex] inverse of [latex]x."[/latex] Keep in mind that

[latex]{f}^{-1}\left(x\right)\ne \frac{1}{f\left(x\right)}[/latex]

and not all functions have inverses.

In our first example we will identify an inverse function from ordered pairs.

Example

If for a particular one-to-one function [latex]f\left(2\right)=4[/latex] and [latex]f\left(5\right)=12[/latex], what are the corresponding input and output values for the inverse function?

Answer:

The inverse function reverses the input and output quantities, so if

[latex]\begin{array}{c}f\left(2\right)=4,\text{ then }{f}^{-1}\left(4\right)=2;\\ f\left(5\right)=12,{\text{ then f}}^{-1}\left(12\right)=5.\end{array}[/latex]

Alternatively, if we want to name the inverse function [latex]g[/latex], then [latex]g\left(4\right)=2[/latex] and [latex]g\left(12\right)=5[/latex].

Analysis of the Solution

Notice that if we show the coordinate pairs in a table form, the input and output are clearly reversed.

[latex]\left(x,f\left(x\right)\right)[/latex] [latex]\left(x,g\left(x\right)\right)[/latex]
[latex]\left(2,4\right)[/latex] [latex]\left(4,2\right)[/latex]
[latex]\left(5,12\right)[/latex] [latex]\left(12,5\right)[/latex]
In the following video we show an example of finding corresponding input and output values given two ordered pairs from functions that are inverses. https://youtu.be/IR_1L1mnpvw

How To: Given two functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex], test whether the functions are inverses of each other.

  1. Substitute [latex]g(x)[/latex] into [latex]f(x)[/latex]. The result must be x. [latex]f\left(g(x)\right)=x[/latex]
  2. Substitute [latex]f(x)[/latex] into [latex]g(x)[/latex]. The result must be x. [latex]g\left(f(x)\right)=x[/latex]

If [latex]f(x)[/latex] and  [latex]g(x)[/latex] are inverses, then  [latex]f(x)=g^{-1}(x)[/latex] and [latex]g(x)=f^{-1}(x)[/latex]

In our next example we will test inverse relationships algebraically.

Example

If [latex]f\left(x\right)=x^2-3[/latex], for [latex]x\ge0[/latex] and [latex]g\left(x\right)=\sqrt{x+3}[/latex], is g the inverse of f?  [latex]g={f}^{-1}?[/latex]

Answer: Substitute [latex]g(x)=\sqrt{x+3}[/latex] into [latex]f(x)[/latex], this means the new variable in [latex]f(x)[/latex] is [latex]\sqrt{x+3}[/latex] so you will substitute that expression where you see x.  Using parentheses helps keep track of things. [latex-display]\begin{array}{c}f\left(\sqrt{x+3}\right)={(\sqrt{x+3})}^2-3\hfill\\=x+3-3\\=x\hfill \end{array}[/latex-display] Our result implies that [latex]g(x)[/latex] is indeed the inverse of [latex]f(x)[/latex].

Answer

[latex-display]g={f}^{-1}[/latex], for [latex]x\ge0[/latex-display]

In the following video we use algebra to determine if two functions are inverses. https://youtu.be/vObCvTOatfQ We will show one more example of how to verify whether you have an inverse algebraically.

Example

If [latex]f\left(x\right)=\frac{1}{x+2}[/latex] and [latex]g\left(x\right)=\frac{1}{x}-2[/latex], is g the inverse of f?  [latex]g={f}^{-1}?[/latex]

Answer: Substitute [latex]g(x)=\frac{1}{x}-2[/latex] into [latex]f(x)[/latex], this means the new variable in [latex]f(x)[/latex] is [latex]\frac{1}{x}-2[/latex] so you will substitute that expression where you see x.  Using parentheses helps keep track of things.

[latex]\begin{array}{c} f\left(\frac{1}{x}-2\right)=\frac{1}{\left(\frac{1}{x}-2\right)+2}\hfill\\=\frac{1}{\frac{1}{x}}\hfill\\={ x }\hfill \end{array}[/latex]

Answer

[latex-display]g={f}^{-1}[/latex-display]

We will show one more example of how to use algebra to determine whether two functions are inverses of each other. https://youtu.be/hzehBtNmw08

 Domain and Range of a Function and It's Inverse

The outputs of the function [latex]f[/latex] are the inputs to [latex]{f}^{-1}[/latex], so the range of [latex]f[/latex] is also the domain of [latex]{f}^{-1}[/latex]. Likewise, because the inputs to [latex]f[/latex] are the outputs of [latex]{f}^{-1}[/latex], the domain of [latex]f[/latex] is the range of [latex]{f}^{-1}[/latex]. We can visualize the situation.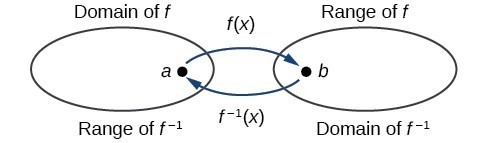
Domain and range of a function and its inverse. Domain and range of a function and its inverse In many cases, if a function is not one-to-one, we can still restrict the function to a part of its domain on which it is one-to-one. For example, we can make a restricted version of the square function [latex]f\left(x\right)={x}^{2}[/latex] with its range limited to [latex]\left[0,\infty \right)[/latex], which is a one-to-one function (it passes the horizontal line test) and which has an inverse (the square-root function).

Domain and Range of Inverse Functions

The range of a function [latex]f\left(x\right)[/latex] is the domain of the inverse function [latex]{f}^{-1}\left(x\right)[/latex].

The domain of [latex]f\left(x\right)[/latex] is the range of [latex]{f}^{-1}\left(x\right)[/latex].

In our last example we will define the domain and range of a function's inverse using a table of values, and evaluate the inverse at a specific value.

Example

A function [latex]f\left(t\right)[/latex] is given below, showing distance in miles that a car has traveled in [latex]t[/latex] minutes.

  1. Define the domain and range of the function and it's inverse.
  2. Find and interpret [latex]{f}^{-1}\left(70\right)[/latex].
[latex]t\text{ (minutes)}[/latex] [latex]30[/latex] [latex]50[/latex] [latex]70[/latex] [latex]90[/latex]
[latex]f\left(t\right)\text{ (miles)}[/latex] [latex]20[/latex] [latex]40[/latex] [latex]60[/latex] [latex]70[/latex]

Answer: 1.Domain and Range of the Original Function The domain of this tabular function, [latex]f\left(t\right)[/latex] , is all the input values, t in minutes:[latex]{30, 50, 70, 90}[/latex] The range of this tabular function,[latex]f\left(t\right)[/latex],  is all the output values[latex]f\left(t\right)[/latex] in miles:[latex] {20, 40, 60, 70}[/latex] Domain and Range of the Inverse Function

The domain for the inverse will be the outputs from the original, so the domain of  [latex]{f}^{-1}(x)[/latex] is the output values from [latex]f\left(t\right)[/latex]: [latex]{20, 40, 60, 70}[/latex]

The range for the inverse will be the inputs from the original: [latex]{30, 50, 70, 90}[/latex] This translates to putting in a number of miles and getting out how long it took to drive that far in minutes. 2. So in the expression [latex]{f}^{-1}\left(70\right)[/latex], [latex]70[/latex] is an output value of the original function, representing [latex]70[/latex] miles. The inverse will return the corresponding input of the original function [latex]f[/latex], [latex]90[/latex] minutes, so [latex]{f}^{-1}\left(70\right)=90[/latex]. The interpretation of this is that, to drive [latex]70[/latex] miles, it took [latex]90[/latex] minutes.

Summary

The inverse of a function can be defined for one-to-one functions.  If a function is not one-to-one, it can be possible to restrict it's domain to make it so. The domain of a function will become the range of it's inverse.  The range of a function will become the domain of it's inverse.  Inverses can be verified using tabular data as well as algebraically.

Licenses & Attributions

CC licensed content, Original

  • Ex 1: Determine if Two Functions Are Inverses. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
  • Ex 2: Determine if Two Functions Are Inverses. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..
  • Ex 1: Composition of Function. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
  • Ex: Function and Inverse Function Values. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.