We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Read: Logarithmic Equations

Learning Objectives

  • Use the definition of a logarithm to solve logarithmic equations
  • Use a graph to verify or analyze the solution to a logarithmic equation
We have already seen that every logarithmic equation [latex]{\mathrm{log}}_{b}\left(x\right)=y[/latex] is equivalent to the exponential equation [latex]{b}^{y}=x[/latex]. We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.

For example, consider the equation [latex]{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3[/latex]. To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for x:

[latex]\begin{array}{c}{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x - 5\right)=3\hfill & \hfill \\ \text{ }{\mathrm{log}}_{2}\left(2\left(3x - 5\right)\right)=3\hfill & \text{Apply the product rule of logarithms}.\hfill \\ \text{ }{\mathrm{log}}_{2}\left(6x - 10\right)=3\hfill & \text{Distribute}.\hfill \\ \text{ }{2}^{3}=6x - 10\hfill & \text{Apply the definition of a logarithm}.\hfill \\ \text{ }8=6x - 10\hfill & \text{Calculate }{2}^{3}.\hfill \\ \text{ }18=6x\hfill & \text{Add 10 to both sides}.\hfill \\ \text{ }x=3\hfill & \text{Divide by 6}.\hfill \end{array}[/latex]
In our first example we will show how to use techniques from solving linear equations to solve a logarithmic equation.

Example

Solve [latex]2\mathrm{ln}x+3=7[/latex].

Answer: [latex]\begin{array}{c}2\mathrm{ln}x+3=7\hfill & \hfill \\ \text{ }2\mathrm{ln}x=4\hfill & \text{Subtract 3}.\hfill \\ \text{ }\mathrm{ln}x=2\hfill & \text{Divide by 2}.\hfill \\ \text{ }x={e}^{2}\hfill & \text{Rewrite in exponential form}.\hfill \end{array}[/latex]

Analysis of the solution

The solution for the previous equation was [latex]x={e}^{2}[/latex], this is often referred to as the exact solution.  Sometimes, you may be asked to give an approximation, which would be more useful to someone using the result for a financial, scientific or engineering application. The approximation for [latex]x={e}^{2}[/latex] can be found with a calculator. [latex]x={e}^{2}\approx{7.4}[/latex] In general, we can describe using the definition of a logarithm to solve logarithmic equations as follows:

For any algebraic expression S and real numbers b and c, where [latex]b>0,\text{ }b\ne 1[/latex],

[latex]{\mathrm{log}}_{b}\left(S\right)=c\text{ if and only if }{b}^{c}=S[/latex]
Here is another example of what you may encounter when solving logarithmic equations.

Example

Solve [latex]2\mathrm{ln}\left(6x\right)=7[/latex].

Answer: [latex]\begin{array}{c}2\mathrm{ln}\left(6x\right)=7\hfill & \hfill \\ \text{ }\mathrm{ln}\left(6x\right)=\frac{7}{2}\hfill & \text{Divide by 2}.\hfill \\ \text{ }6x={e}^{\left(\frac{7}{2}\right)}\hfill & \text{Use the definition of }\mathrm{ln}.\hfill \\ \text{ }x=\frac{1}{6}{e}^{\left(\frac{7}{2}\right)}\hfill & \text{Divide by 6}.\hfill \end{array}[/latex]

Answer

Exact answer: [latex]x=\frac{1}{6}{e}^{\left(\frac{7}{2}\right)}[/latex] Approximate answer: [latex]x\approx{5.5}[/latex]

In our next example we will show you the power of using graphs to analyze solutions to logarithmic equations. By turning each side of the equation into a function and plotting them on the same set of axes, we can see how they interact with each other.  In this case, we get a logarithmic function and a horizontal line, and find that the solution is the point where the two intersect.

Example

Solve [latex]\mathrm{ln}x=3[/latex].

Answer:

[latex]\begin{array}{c}\mathrm{ln}x=3\hfill & \hfill \\ x={e}^{3}\hfill & \text{Use the definition of the natural logarithm}\text{.}\hfill \end{array}[/latex]

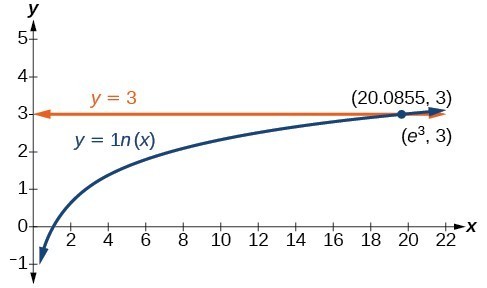
The graph below represents the graph of the equation. On the graph, the x-coordinate of the point at which the two graphs intersect is close to 20. In other words [latex]{e}^{3}\approx 20[/latex]. A calculator gives a better approximation: [latex]{e}^{3}\approx 20.0855[/latex].

Graph of two questions, y=3 and y=ln(x), which intersect at the point (e^3, 3) which is approximately (20.0855, 3).
 The graphs of [latex]y=\mathrm{ln}x[/latex] and y = 3 cross at the point [latex]\left(e^3,3\right)[/latex], which is approximately (20.0855, 3).

In the same way that a story can help you understand a complex concept, graphs can help us understand a wide variety of concepts in mathematics. Visual representations of the parts of an equation can be created by turning each side into a function and plotting the functions on the same set of axes.

Use the one-to-one property of logarithms to solve logarithmic equations

As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers  [latex]<em>x </em>> 0, <em>S </em>> 0, <em>T </em>> 0[/latex] and any positive real number b, where [latex]b\ne 1[/latex],

[latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex].

For example,

[latex]\text{If }{\mathrm{log}}_{2}\left(x - 1\right)={\mathrm{log}}_{2}\left(8\right),\text{then }x - 1=8[/latex].

So, if [latex]x - 1=8[/latex], then we can solve for x, and we get [latex]<em>x </em>= 9[/latex]. To check, we can substitute  [latex]<em>x </em>= 9[/latex] into the original equation: [latex]{\mathrm{log}}_{2}\left(9 - 1\right)={\mathrm{log}}_{2}\left(8\right)=3[/latex]. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.

Example

Solve [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex] Check your results.

Answer: [latex]\begin{array}{c}\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)\hfill & \hfill \\ \text{ }\mathrm{log}\left(\frac{3x - 2}{2}\right)=\mathrm{log}\left(x+4\right)\hfill & \text{Apply the quotient rule of logarithms}.\hfill \\ \text{ }\frac{3x - 2}{2}=x+4\hfill & \text{Apply the one to one property of a logarithm}.\hfill \\ \text{ }3x - 2=2x+8\hfill & \text{Multiply both sides of the equation by }2.\hfill \\ \text{ }x=10\hfill & \text{Subtract 2}x\text{ and add 2}.\hfill \end{array}[/latex]

To check the result, substitute  [latex]<em>x </em>= 10[/latex] into [latex]\mathrm{log}\left(3x - 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)[/latex].

[latex]\begin{array}{c}\mathrm{log}\left(3\left(10\right)-2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(\left(10\right)+4\right)\hfill & \hfill \\ \text{ }\mathrm{log}\left(28\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(14\right)\hfill & \hfill \\ \text{ }\mathrm{log}\left(\frac{28}{2}\right)=\mathrm{log}\left(14\right)\hfill & \text{The solution checks}.\hfill \end{array}[/latex]

Answer

[latex-display]x = 10[/latex-display]

Note, when solving an equation involving logarithms, always check to see if the answer is correct or if there is an extraneous solution. In general, we can summarize solving logarithmic equations as follows: For [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex]
  1. Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form [latex]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T[/latex].
  2. Use the one-to-one property to set the arguments equal.
  3. Solve the resulting equation,  [latex]S = T[/latex], for the unknown.

Example

[latex-display]{\mathrm{log}}_{b}S={\mathrm{log}}_{b}T\text{ if and only if }S=T[/latex-display]

Answer: [latex]\begin{array}{c}\text{ }\mathrm{ln}\left({x}^{2}\right)=\mathrm{ln}\left(2x+3\right)\hfill & \hfill \\ \text{ }{x}^{2}=2x+3\hfill & \text{Use the one-to-one property of the logarithm}.\hfill \\ \text{ }{x}^{2}-2x - 3=0\hfill & \text{Get zero on one side before factoring}.\hfill \\ \left(x - 3\right)\left(x+1\right)=0\hfill & \text{Factor using FOIL}.\hfill \\ \text{ }x - 3=0\text{ or }x+1=0\hfill & \text{If a product is zero, one of the factors must be zero}.\hfill \\ \text{ }x=3\text{ or }x=-1\hfill & \text{Solve for }x.\hfill \end{array}[/latex]

Analysis of the Solution

There are two solutions:  [latex]<em>x </em>= 3 or <em>x </em>= –1[/latex]. The solution  [latex]<em>x </em>= –1[/latex] is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.

Summary

We can combine the definitions of logarithms and algebraic tools used for solving linear equations to solve logarithmic equations.  Graphing each side of a logarithmic equation helps you analyze the solution.

Licenses & Attributions

CC licensed content, Shared previously

  • Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution. License terms: Download For Free at : http://cnx.org/contents/[email protected]..