Read: Solution Sets of Inequalities
Learning Objectives
- Identify whether an ordered pair is in the solution set of a linear inequality
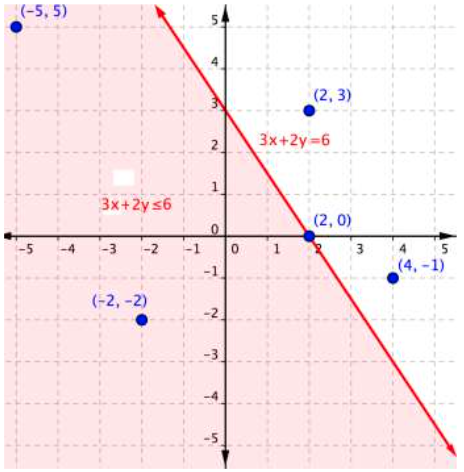 You can substitute the x- and y-values in each of the [latex](x,y)[/latex] ordered pairs into the inequality to find solutions. Sometimes making a table of values makes sense for more complicated inequalities.
You can substitute the x- and y-values in each of the [latex](x,y)[/latex] ordered pairs into the inequality to find solutions. Sometimes making a table of values makes sense for more complicated inequalities.
| Ordered Pair | Makes the inequality [latex-display]3x+2y\leq6[/latex-display] a true statement | Makes the inequality [latex-display]3x+2y\leq6[/latex-display] a false statement |
|---|---|---|
| [latex](−5, 5)[/latex] | [latex]\begin{array}{r}3\left(−5\right)+2\left(5\right)\leq6\\−15+10\leq6\\−5\leq6\end{array}[/latex] | |
| [latex](−2,−2)[/latex] | [latex]\begin{array}{r}3\left(−2\right)+2\left(–2\right)\leq6\\−6+\left(−4\right)\leq6\\–10\leq6\end{array}[/latex] | |
| [latex](2,3)[/latex] | [latex]\begin{array}{r}3\left(2\right)+2\left(3\right)\leq6\\6+6\leq6\\12\leq6\end{array}[/latex] | |
| [latex](2,0)[/latex] | [latex]\begin{array}{r}3\left(2\right)+2\left(0\right)\leq6\\6+0\leq6\\6\leq6\end{array}[/latex] | |
| [latex](4,−1)[/latex] | [latex]\begin{array}{r}3\left(4\right)+2\left(−1\right)\leq6\\12+\left(−2\right)\leq6\\10\leq6\end{array}[/latex] |
Example
Use the graph to determine which ordered pairs plotted below are solutions of the inequality [latex]x–y<3[/latex].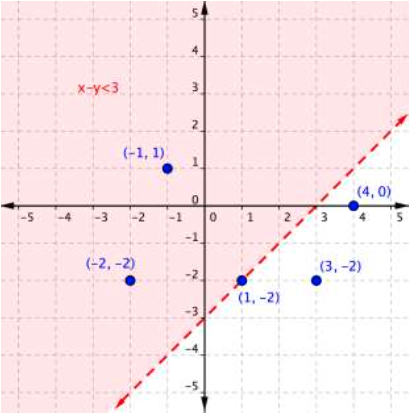
Answer: Solutions will be located in the shaded region. Since this is a “less than” problem, ordered pairs on the boundary line are not included in the solution set. These values are located in the shaded region, so are solutions. (When substituted into the inequality [latex]x–y<3[/latex], they produce true statements.)
[latex](−1,1)[/latex]
[latex](−2,−2)[/latex]
These values are not located in the shaded region, so are not solutions. (When substituted into the inequality [latex]x-y<3[/latex], they produce false statements.)[latex](1,−2)[/latex]
[latex](3,−2)[/latex]
[latex](4,0)[/latex]
Answer
[latex](−1,1)\,\,\,(−2,−2)[/latex]Example
Is [latex](2,−3)[/latex] a solution of the inequality [latex]y<−3x+1[/latex]?Answer: If [latex](2,−3)[/latex] is a solution, then it will yield a true statement when substituted into the inequality [latex]y<−3x+1[/latex].
[latex]y<−3x+1[/latex]
Substitute [latex]x=2[/latex] and [latex]y=−3[/latex] into inequality.[latex]−3<−3\left(2\right)+1[/latex]
Evaluate.[latex]\begin{array}{l}−3<−6+1\\−3<−5\end{array}[/latex]
This statement is not true, so the ordered pair [latex](2,−3)[/latex] is not a solution.Answer
[latex](2,−3)[/latex] is not a solution.Licenses & Attributions
CC licensed content, Shared previously
- Use a Graph Determine Ordered Pair Solutions of a Linear Inequalty in Two Variable. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Determine if Ordered Pairs Satisfy a Linear Inequality. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Unit 13: Graphing, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
