We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Intermediate Algebra

Read: Graphs of Polynomial Functions

[latex]Learning Objectives

  • Identify graphs of polynomial functions
  • Use the degree and leading coefficient to describe the behavior of the graph of a polynomial functions
Plotting polynomial functions using tables of values can be misleading because of some of the inherent characteristics of polynomials. Additionally, the algebra of finding points like x-intercepts for higher degree polynomials can get very messy and oftentimes impossible to find by hand. We have therefore developed some techniques for describing the general behavior of polynomial graphs. Polynomial functions of degree [latex]2[/latex] or more have graphs that do not have sharp corners these types of graphs are called smooth curves. Polynomial functions also display graphs that have no breaks. Curves with no breaks are called continuous. The figure below shows a graph that represents a polynomial function and a graph that represents a function that is not a polynomial. 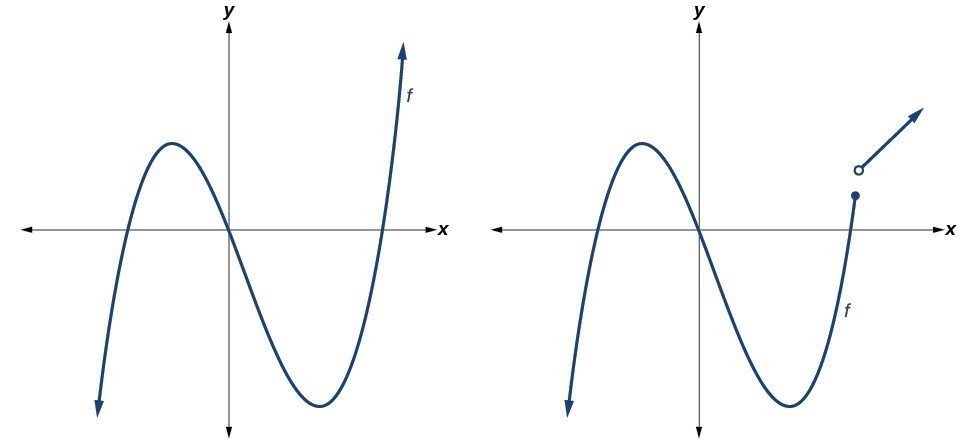Graph of f(x)=x^3-0.01x. Now you try it.

Example

Which of the graphs below represents a polynomial function?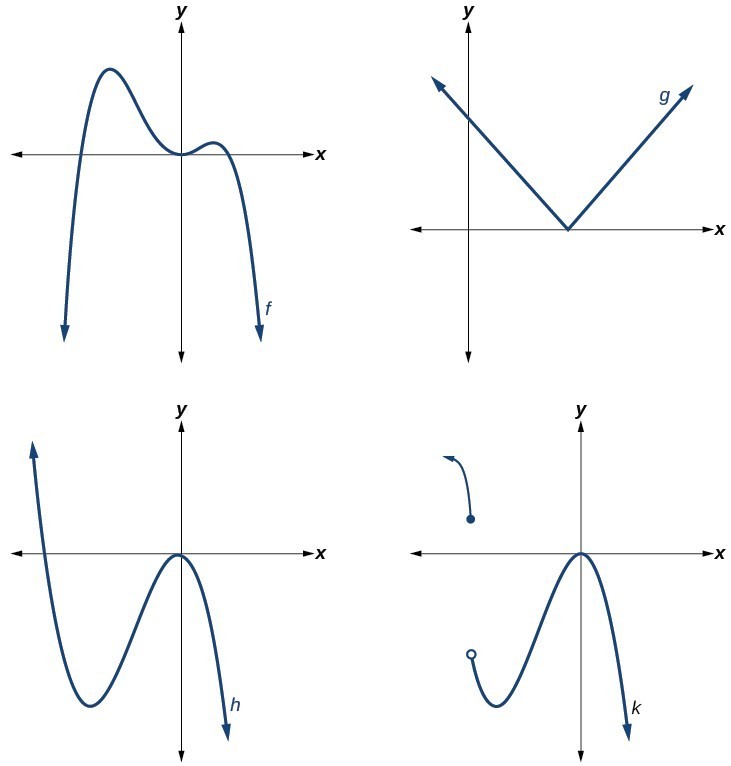 Two graphs in which one has a polynomial function and the other has a function closely resembling a polynomial but is not.

Answer:

The graphs of f and h are graphs of polynomial functions. They are smooth and continuous.

The graphs of g and k are graphs of functions that are not polynomials. The graph of function g has a sharp corner. The graph of function k is not continuous.

 

Q & A

Do all polynomial functions have as their domain all real numbers?

Yes. Any real number is a valid input for a polynomial function.

Identifying the shape of the graph of a polynomial function

Knowing the degree of a polynomial function is useful in helping us predict what it's graph will look like. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as x gets very large or very small, so its behavior will dominate the graph. For any polynomial, the graph of the polynomial will match the end behavior of the term of highest degree.

As an example we compare the outputs of a degree [latex]2[/latex] polynomial and a degree [latex]5[/latex] polynomial in the following table.
x [latex]f(x)=2x^2-2x+4[/latex] [latex]g(x)=x^5+2x^3-12x+3[/latex]
[latex]1[/latex] [latex]4[/latex] [latex]8[/latex]
[latex]10[/latex] [latex]184[/latex] [latex]98117[/latex]
[latex]100[/latex] [latex]19804[/latex] [latex]9998001197[/latex]
[latex]1000[/latex] [latex]1998004[/latex] [latex]9999980000000000[/latex]
As the inputs for both functions get larger, the degree [latex]5[/latex] polynomial outputs get much larger than the degree [latex]2[/latex] polynomial outputs. This is why we use the leading term to get a rough idea of the behavior of polynomial graphs. There are two other important features of polynomials that influence the shape of it's graph. The first  is whether the degree is even or odd, and the second is whether the leading term is negative.

Even degree polynomials

In the figure below, we show the graphs of [latex]f\left(x\right)={x}^{2},g\left(x\right)={x}^{4}[/latex] and [latex]\text{and}h\left(x\right)={x}^{6}[/latex], which are all have even degrees. Notice that these graphs have similar shapes, very much like that of a quadratic function. However, as the power increases, the graphs flatten somewhat near the origin and become steeper away from the origin.

Graph of three functions, h(x)=x^2 in green, g(x)=x^4 in orange, and f(x)=x^6 in blue.

Odd degree polynomials

The next figure shows the graphs of [latex]f\left(x\right)={x}^{3},g\left(x\right)={x}^{5},\text{and}h\left(x\right)={x}^{7}[/latex], which are all odd degree functions. Graph of three functions, f(x)=x^3 in green, g(x)=x^5 in orange, and h(x)=x^7 in blue.

Notice that one arm of the graph points down and the other points up.  This is because when your input is negative, you will get a negative output if the degree is odd. The following table of values shows this.

x [latex]f(x)=x^4[/latex] [latex]h(x)=x^5[/latex]
[latex]-1[/latex] [latex]1[/latex] [latex]-1[/latex]
[latex]-2[/latex] [latex]16[/latex] [latex]-32[/latex]
[latex]-3[/latex] [latex]81[/latex] [latex]-243[/latex]
Now you try it.

Example

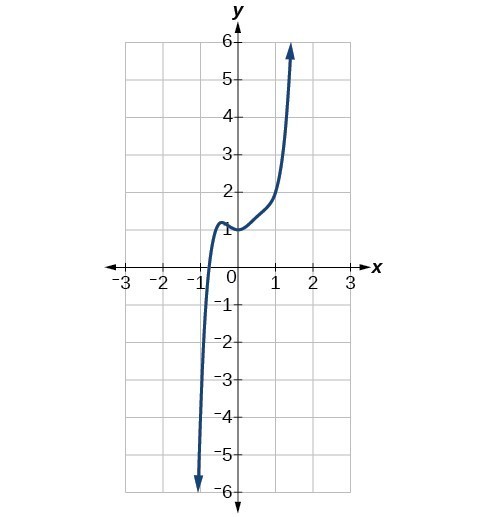
Identify whether graph represents a polynomial function that has a degree that is even or odd. a) Graph of f(x)=5x^4+2x^3-x-4. b) Graph of f(x)=3x^5-4x^4+2x^2+1.

Answer: a) Both arms of this polynomial point upward, similar to a quadratic polynomial, therefore the degree must be even.  If you apply negative inputs to an even degree polynomial you will get positive outputs back. b) As the inputs of this polynomial become more negative the outputs also become negative, the only way this is possible is with an odd degree polynomial. Therefore, this polynomial must have odd degree. Put Answer Here

 The sign of the leading term

What would happen if we change the sign of the leading term of an even degree polynomial?  For example, let's say that the leading term of a polynomial is [latex]-3x^4[/latex].  We will use a table of values to compare the outputs for a polynomial with leading term [latex]-3x^4[/latex], and [latex]3x^4[/latex].
x [latex]-3x^4[/latex] [latex]3x^4[/latex]
[latex]-2[/latex] [latex]-48[/latex] [latex]48[/latex]
[latex]-1[/latex] [latex]-3[/latex] [latex]3[/latex]
[latex]0[/latex] [latex]0[/latex] [latex]0[/latex]
[latex]1[/latex] [latex]-3[/latex] [latex]3[/latex]
[latex]2[/latex] [latex]-48[/latex] [latex]48[/latex]
Plotting these points on a grid leads to this plot, the red points indicate a negative leading coefficient, and the blue points indicate a positive leading coefficient: Screen Shot 2016-07-15 at 2.21.36 PM The negative sign creates a reflection of [latex]3x^4[/latex] across the x-axis.  The arms of a polynomial with a leading term of [latex]-3x^4[/latex] will point down, whereas the arms of a polynomial with leading term [latex]3x^4[/latex] will point up. Now you try it.

Example

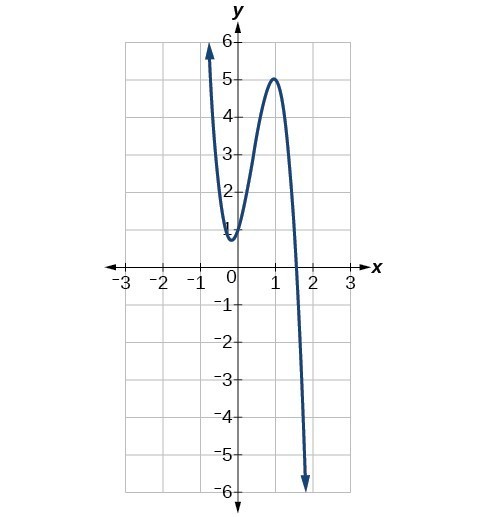
Identify whether the leading term is positive or negative and whether the degree is even or odd for the following graphs of polynomial functions. a) Graph of f(x)=-2x^6-x^5+3x^4+x^3. b) Graph of f(x)=-6x^3+7x^2+3x+1.

Answer: a) Both arms of this polynomial point in the same direction so it must have an even degree.  The leading term of the polynomial must be negative since the arms are pointing downward. b) The arms of this polynomial point in different directions, so the degree must be odd. As the inputs get really big and positive, the outputs get really big and negative, so the leading coefficient must be negative.

 

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • College Algebra. Provided by: OpenStax Authored by: Abramson, Jay, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: Public Domain: No Known Copyright. License terms: Download for free at: http://cnx.org/contents/[email protected].