Read: Define and Evaluate Polynomials
Learning Objectives
- Identify the degree and leading coefficient of a polynomial
- Evaluate a polynomial for given values
| IS a Polynomial | Is NOT a Polynomial | Because |
| [latex]2x^2-\frac{1}{2}x -9[/latex] | [latex]\frac{2}{x^{2}}+x[/latex] | Polynomials only have variables in the numerator |
| [latex]\frac{y}{4}-y^3[/latex] | [latex]\frac{2}{y}+4[/latex] | Polynomials only have variables in the numerator |
| [latex]\sqrt{12}\left(a\right)+9[/latex] | [latex]\sqrt{a}+7[/latex] | Roots are equivalent to rational exponents, and polynomials only have integer exponents |
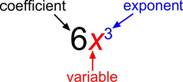 A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial. A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial.
We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers are descending, we say that it is in standard form. It is important to note that polynomials only have integer exponents.
A polynomial containing two terms, such as [latex]2x - 9[/latex], is called a binomial. A polynomial containing three terms, such as [latex]-3{x}^{2}+8x - 7[/latex], is called a trinomial.
We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. The term with the highest degree is called the leading term because it is usually written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written so that the powers are descending, we say that it is in standard form. It is important to note that polynomials only have integer exponents.
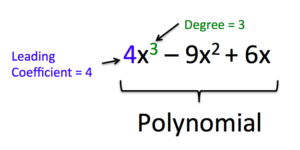
Given a polynomial expression, identify the degree and leading coefficient.
- Find the highest power of x to determine the degree.
- Identify the term containing the highest power of x to find the leading term.
- Identify the coefficient of the leading term.
Example
For the following polynomials, identify the degree, the leading term, and the leading coefficient.- [latex]3+2{x}^{2}-4{x}^{3}[/latex]
- [latex]5{t}^{5}-2{t}^{3}+7t[/latex]
- [latex]6p-{p}^{3}-2[/latex]
Answer:
- The highest power of x is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]-4[/latex].
- The highest power of t is [latex]5[/latex], so the degree is [latex]5[/latex]. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, [latex]5[/latex].
- The highest power of p is [latex]3[/latex], so the degree is [latex]3[/latex]. The leading term is the term containing that degree, [latex]-{p}^{3}[/latex], The leading coefficient is the coefficient of that term, [latex]-1[/latex].
| Monomials | Binomials | Trinomials | Other Polynomials |
| [latex]15[/latex] | [latex]3y+13[/latex] | [latex]x^{3}-x^{2}+1[/latex] | [latex]5x^{4}+3x^{3}-6x^{2}+2x[/latex] |
| [latex] \displaystyle \frac{1}{2}x[/latex] | [latex]4p-7[/latex] | [latex]3x^{2}+2x-9[/latex] | [latex]\frac{1}{3}x^{5}-2x^{4}+\frac{2}{9}x^{3}-x^{2}+4x-\frac{5}{6}[/latex] |
| [latex]-4y^{3}[/latex] | [latex]3x^{2}+\frac{5}{8}x[/latex] | [latex]3y^{3}+y^{2}-2[/latex] | [latex]3t^{3}-3t^{2}-3t-3[/latex] |
| [latex]16n^{4}[/latex] | [latex]14y^{3}+3y[/latex] | [latex]a^{7}+2a^{5}-3a^{3}[/latex] | [latex]q^{7}+2q^{5}-3q^{3}+q[/latex] |
Evaluate a polynomial
You can evaluate polynomials just as you have been evaluating expressions all along. To evaluate an expression for a value of the variable, you substitute the value for the variable every time it appears. Then use the order of operations to find the resulting value for the expression.Example
Evaluate [latex]3x^{2}-2x+1[/latex] for [latex]x=-1[/latex].Answer: Substitute [latex]-1[/latex] for each x in the polynomial.
[latex]3\left(-1\right)^{2}-2\left(-1\right)+1[/latex]
Following the order of operations, evaluate exponents first.[latex]3\left(1\right)-2\left(-1\right)+1[/latex]
Multiply [latex]3[/latex] times [latex]1[/latex], and then multiply [latex]-2[/latex] times [latex]-1[/latex].[latex]3+\left(-2\right)\left(-1\right)+1[/latex]
Change the subtraction to addition of the opposite.[latex]3+2+1[/latex]
Find the sum.Answer
[latex-display]3x^{2}-2x+1=6[/latex], for [latex]x=-1[/latex-display]Example
Evaluate [latex] \displaystyle -\frac{2}{3}p^{4}+2^{3}-p[/latex] for [latex]p = 3[/latex].Answer: Substitute [latex]3[/latex] for each p in the polynomial.
[latex] \displaystyle -\frac{2}{3}\left(3\right)^{4}+2\left(3\right)^{3}-3[/latex]
Following the order of operations, evaluate exponents first and then multiply.[latex] \displaystyle -\frac{2}{3}\left(81\right)+2\left(27\right)-3[/latex]
Add and then subtract to get [latex]-3[/latex].[latex]-54 + 54 – 3[/latex]
Answer
[latex-display] \displaystyle -\frac{2}{3}p^{4}+2p^{3}-p=-3[/latex], for [latex]p = 3[/latex-display]IN the following video we show more examples of evaluating polynomials for given values of the variable.
https://youtu.be/2EeFrgQP1hMLicenses & Attributions
CC licensed content, Original
- Evaluate a Polynomial in One Variable. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology Located at: https://www.nroc.org/. License: CC BY: Attribution.
- College Algebra. Authored by: Abramson, Jay, et al.. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: Public Domain: No Known Copyright. License terms: Download for free at :http://cnx.org/contents/[email protected]:1/Preface.
- Ex: Intro to Polynomials in One Variable. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
