Read: Divide Polynomials Part I
Learning Objectives
- Divide a polynomial by a binomial
Divide a polynomial by a binomial
Dividing a polynomial by a monomial can be handled by dividing each term in the polynomial separately. This can’t be done when the divisor has more than one term. However, the process of long division can be very helpful with polynomials. Recall how you can use long division to divide two whole numbers, say [latex]900[/latex] divided by [latex]37[/latex].[latex]37\overline{)900}[/latex]
First, you would think about how many [latex]37s[/latex] are in [latex]90[/latex], as [latex]9[/latex] is too small. (Note: you could also think, how many [latex]40s[/latex] are there in [latex]90[/latex].)
[latex]\begin{array}\,\,\,\,\,\,\,\,\,\,\,\,2\\37\overline{)900}\\\,\,\,\,\,\,\,\,74\end{array}[/latex]
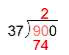There are two [latex]37s[/latex] in [latex]90[/latex], so write [latex]2[/latex] above the last digit of [latex]90[/latex]. Two [latex]37s[/latex] is [latex]74[/latex]; write that product below the [latex]90[/latex].
[latex]\begin{array}\,\,\,\,\,\,\,\,\,\,\,\,2\\37\overline{)900}\\\,\,\,\,\,\underline{-74}\\\,\,\,\,\,\,\,16\end{array}[/latex]
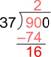Subtract: [latex]90–74[/latex] is [latex]16[/latex]. (If the result is larger than the divisor, [latex]37[/latex], then you need to use a larger number for the quotient.)
[latex]\begin{array}\,\,\,\,\,\,\,\,\,\,\,\,2\\37\overline{)900}\\\,\,\,\,\,\underline{-74}\\\,\,\,\,\,\,\,160\end{array}[/latex]
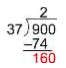Bring down the next digit [latex](0)[/latex] and consider how many [latex]37s[/latex] are in [latex]160[/latex].
[latex]\begin{array}\,\,\,\,\,\,\,\,\,\,\,\,2\\37\overline{)900}\\\,\,\,\,\,\underline{-74}\\\,\,\,\,\,\,\,160\\\,\,\,\underline{-148}\end{array}[/latex]
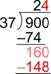There are four [latex]37s[/latex] in [latex]160[/latex], so write the [latex]4[/latex] next to the two in the quotient. Four [latex]37s[/latex] is [latex]148[/latex]; write that product below the [latex]160[/latex].
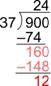Subtract: [latex]160–148[/latex] is [latex]12[/latex]. This is less than [latex]37[/latex] so the [latex]4[/latex] is correct. Since there are no more digits in the dividend to bring down, you’re done.
The final answer is [latex]24[/latex] R[latex]12[/latex], or [latex]24\frac{12}{37}[/latex]. You can check this by multiplying the quotient (without the remainder) by the divisor, and then adding in the remainder. The result should be the dividend:
[latex]24\cdot37+12=888+12=900[/latex]
To divide polynomials, use the same process. This example shows how to do this when dividing by a binomial.Example
Divide: [latex]\frac{\left(x^{2}–4x–12\right)}{\left(x+2\right)}[/latex]Answer: How many x’s are there in [latex]x^{2}[/latex]? That is, what is [latex] \frac{{{x}^{2}}}{x}[/latex]?
[latex] \frac{{{x}^{2}}}{x}=x[/latex]. Put x in the quotient above the [latex]-4x[/latex] term. (These are like terms, which helps to organize the problem.)
Write the product of the divisor and the part of the quotient you just found under the dividend. Since [latex]x\left(x+2\right)=x^{2}+2x[/latex], write this underneath, and get ready to subtract.
Rewrite [latex]–\left(x^{2} + 2x\right)[/latex] as its opposite [latex]–x^{2}–2x[/latex] so that you can add the opposite. (Adding the opposite is the same as subtracting, and it is easier to do.)
Add [latex]-x^{2}[/latex] to [latex]x^{2}[/latex], and [latex]-2x[/latex] to [latex]-4x[/latex].
Bring down [latex]-12[/latex].
Repeat the process. How many times does x go into [latex]-6x[/latex]? In other words, what is [latex] \frac{-6x}{x}[/latex]?
Since [latex] \frac{-6x}{x}=-6[/latex], write [latex]-6[/latex] in the quotient. Multiply [latex]-6[/latex] and [latex]x+2[/latex] and prepare to subtract the product.
Rewrite [latex]–\left(-6x–12\right)[/latex] as [latex]6x+12[/latex], so that you can add the opposite.
Add. In this case, there is no remainder, so you’re done.
Answer
[latex-display]\frac{\left(x^{2}–4x–12\right)}{\left(x+2\right)}=x–6[/latex-display][latex]\left(x-6\right)\left(x+2\right)=x^{2}+2x-6x-12=x^{2}-4x-12[/latex]
In this video we show another example of dividing a degree two trinomial by a degree one binomial. https://youtu.be/KUPFg__Djzw Let’s try another example. In this example, a term is “missing” from the dividend.Example
Divide: [latex]\frac{\left(x^{3}–6x–10\right)}{\left(x–3\right)}[/latex]Answer: In setting up this problem, notice that there is an [latex]x^{3}[/latex] term but no [latex]x^{2}[/latex] term. Add [latex]0x^{2}[/latex] as a “place holder” for this term. (Since 0 times anything is 0, you’re not changing the value of the dividend.)
Focus on the first terms again: how many x’s are there in [latex]x^{3}[/latex]? Since [latex] \frac{{{x}^{3}}}{x}=x^{2}[/latex], put [latex]x^{2}[/latex] in the quotient.
Multiply [latex]x^{2}\left(x–3\right)=x^{3}–3x^{2}[/latex], write this underneath the dividend, and prepare to subtract.
Rewrite the subtraction using the opposite of the expression [latex]x^{3}-3x^{2}[/latex]. Then add.
Bring down the rest of the expression in the dividend. It’s helpful to bring down all of the remaining terms.
Now, repeat the process with the remaining expression, [latex]3x^{2}-6x–10[/latex], as the dividend.
Remember to watch the signs!
How many x’s are there in [latex]3[/latex]x? Since there are [latex]3[/latex], multiply [latex]3\left(x–3\right)=3x–9[/latex], write this underneath the dividend, and prepare to subtract.
Continue until the degree of the remainder is less than the degree of the divisor. In this case the degree of the remainder, [latex]-1[/latex], is [latex]0[/latex], which is less than the degree of [latex]x-3[/latex], which is [latex]1[/latex].
Also notice that you have brought down all the terms in the dividend, and that the quotient extends to the right edge of the dividend. These are other ways to check whether you have completed the problem.
You can write the remainder using the symbol R, or as a fraction added to the rest of the quotient with the remainder in the numerator and the divisor in the denominator. In this case, since the remainder is negative, you can also subtract the opposite.
Answer
[latex-display]\begin{array}{r}{\left(x^{3}–6x–10\right)}{\left(x–3\right)}=x^{2}+3x+3+R-1,\\x^{2}+3x+3+\frac{-1}{x-3}, \text{ or }\\x^{2}+3x+3-\frac{1}{x-3}\end{array}[/latex-display][latex]\left(x–3\right)\left(x^{2}+3x+3\right)\,\,\,=\,\,\,x\left(x^{2}+3x+3\right)–3\left(x^{2}+3x+3\right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\,\,\,x^{3}+3x^{2}+3x–3x^{2}–9x–9\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\,\,\,x^{3}–6x–9\\\,\,\,\,\,\,\,\,x^{3}–6x–9+\left(-1\right)\,\,\,=\,\,\,x^{3}–6x–10[/latex]
In the video that follows, we show another example of dividing a degree three trinomial by a binomial, not the "missing" term and how we work with it. https://youtu.be/Rxds7Q_UTeo The process above works for dividing any polynomials, no matter how many terms are in the divisor or the dividend. The main things to remember are:- When subtracting, be sure to subtract the whole expression, not just the first term. This is very easy to forget, so be careful!
- Stop when the degree of the remainder is less than the degree of the dividend, or when you have brought down all the terms in the dividend, and that the quotient extends to the right edge of the dividend.
Summary
Dividing polynomials by polynomials of more than one term can be done using a process very much like long division of whole numbers. You must be careful to subtract entire expressions, not just the first term. Stop when the degree of the remainder is less than the degree of the divisor. The remainder can be written using R notation, or as a fraction added to the quotient with the remainder in the numerator and the divisor in the denominator.Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: Public Domain: No Known Copyright.
- Divide a Degree 3 Polynomial by a Degree 1 Polynomial (Long Division with Missing Term). Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Lumen Learning License: CC BY: Attribution.
- Ex 1: Divide a Trinomial by a Binomial Using Long Division. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- Ex 6: Divide a Polynomial by a Degree Two Binomial Using Long Division. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
