Read: Graph Using Intercepts
Learning Objectives
- Recognize when an ordered pair is a y-intercept or an x-intercept
- Graph a linear equation using x- and y-intercepts
Intercepts
The intercepts of a line are the points where the line intercepts, or crosses, the horizontal and vertical axes. To help you remember what “intercept” means, think about the word “intersect.” The two words sound alike and in this case mean the same thing. The straight line on the graph below intercepts the two coordinate axes. The point where the line crosses the x-axis is called the x-intercept. The y-intercept is the point where the line crosses the y-axis.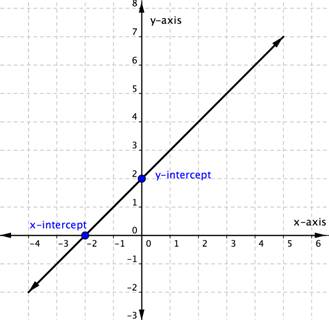
The x-intercept above is the point [latex](−2,0)[/latex]. The y-intercept above is the point ([latex]0, 2[/latex]).
Notice that the y-intercept always occurs where [latex]x=0[/latex], and the x-intercept always occurs where [latex]y=0[/latex].
To find the x- and y-intercepts of a linear equation, you can substitute [latex]0[/latex] for y and for x respectively.
For example, the linear equation [latex]3y+2x=6[/latex] has an x intercept when [latex]y=0[/latex], so [latex]3\left(0\right)+2x=6[/latex].
[latex]\begin{array}{r}2x=6\\x=3\end{array}[/latex]
The x-intercept is [latex](3,0)[/latex]. Likewise the y-intercept occurs when [latex]x=0[/latex].[latex]\begin{array}{r}3y+2\left(0\right)=6\\3y=6\\y=2\end{array}[/latex]
The y-intercept is [latex](0,2)[/latex].Using Intercepts to Graph Lines
You can use intercepts to graph linear equations. Once you have found the two intercepts, draw a line through them. Let’s do it with the equation [latex]3y+2x=6[/latex]. You figured out that the intercepts of the line this equation represents are [latex](0,2)[/latex] and [latex](3,0)[/latex]. That’s all you need to know.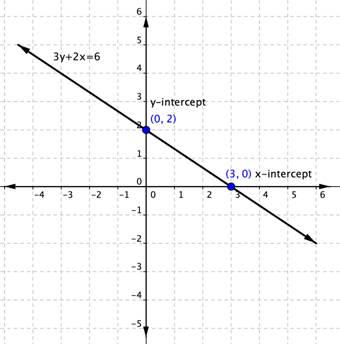
Example
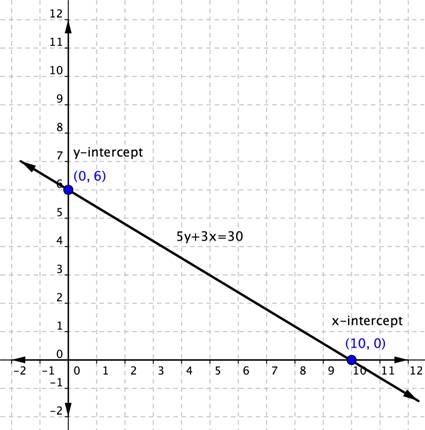
Graph [latex]5y+3x=30[/latex] using the x and y-intercepts.Answer: When an equation is in [latex]Ax+By=C[/latex] form, you can easily find the x- and y-intercepts and then graph.
[latex]\begin{array}{r}5y+3x=30\\5y+3\left(0\right)=30\\5y+0=30\\5y=30\\y=\,\,\,6\\y\text{-intercept}\,\left(0,6\right)\end{array}[/latex]
To find the y-intercept, set [latex]x=0[/latex] and solve for y.[latex]\begin{array}{r}5y+3x=30\\5\left(0\right)+3x=30\\0+3x=30\\3x=30\\x=10\\x\text{-intercept}\left(10,0\right)\end{array}[/latex]
To find the x-intercept, set [latex]y=0[/latex] and solve for x.Answer
Example
Graph [latex]y=2x-4[/latex] using the x and y-intercepts.Answer: First, find the y-intercept. Set x equal to zero and solve for y.
[latex]\begin{array}{l}y=2x-4\\y=2\left(0\right)-4\\y=0-4\\y=-4\\y\text{-intercept}\left(0,-4\right)\end{array}[/latex]
To find the x-intercept, set [latex]y=0[/latex] and solve for x.[latex]\begin{array}{l}y=2x-4\\0=2x-4\\4=2x\\x=2\\x\text{-intercept}\left(2,0\right)\end{array}[/latex]
Answer
