Read: Solve an Application Using a Formula
Learning Objectives
- Solve distance, rate, and time problems
- Solve area, volume, and perimeter problems
- Solve temperature conversion problems
- Rearrange formulas to isolate specific variables
- Identify an unknown given a formula
Distance, Rate, and Time
Example
It takes Andrew [latex]30[/latex] min to drive to work in the morning. He drives home using the same route, but it takes [latex]10[/latex] min longer, and he averages [latex]10 mi/h[/latex] less than in the morning. How far does Andrew drive to work?Answer: This is a distance problem, so we can use the formula [latex]d=rt[/latex], where distance equals rate multiplied by time. Note that when rate is given in mi/h, time must be expressed in hours. Consistent units of measurement are key to obtaining a correct solution. First, we identify the known and unknown quantities. Andrew’s morning drive to work takes [latex]30[/latex] min, or [latex]\Large\frac{1}{2}[/latex] h at rate [latex]r[/latex]. His drive home takes [latex]40[/latex] min, or [latex]\Large\frac{2}{3}[/latex] h, and his speed averages [latex]10 mi/h[/latex] less than the morning drive. Both trips cover distance [latex]d[/latex]. A table, such as the one below, is often helpful for keeping track of information in these types of problems.
| [latex]d[/latex] | [latex]r[/latex] | [latex]t[/latex] | |
|---|---|---|---|
| To Work | [latex]d[/latex] | [latex]r[/latex] | [latex]\Large\frac{1}{2}[/latex] |
| To Home | [latex]d[/latex] | [latex]r - 10[/latex] | [latex]\Large\frac{2}{3}[/latex] |
Example
The perimeter of a rectangular outdoor patio is [latex]54[/latex] ft. The length is [latex]3[/latex] ft greater than the width. What are the dimensions of the patio?Answer: The perimeter formula is standard: [latex]P=2L+2W[/latex]. We have two unknown quantities, length and width. However, we can write the length in terms of the width as [latex]L=W+3[/latex]. Substitute the perimeter value and the expression for length into the formula. It is often helpful to make a sketch and label the sides.
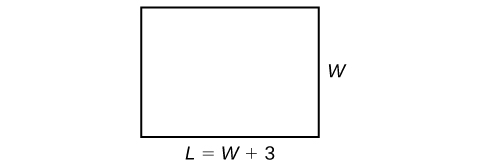 Figure 3
Figure 3Example
The perimeter of a tablet of graph paper is [latex]48[/latex] in. The length is [latex]6[/latex] in. more than the width. Find the area of the graph paper.Answer: The standard formula for area is [latex]A=LW[/latex]; however, we will solve the problem using the perimeter formula. The reason we use the perimeter formula is because we know enough information about the perimeter that the formula will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem such as this one. We know that the length is [latex]6[/latex] in. more than the width, so we can write length as [latex]L=W+6[/latex]. Substitute the value of the perimeter and the expression for length into the perimeter formula and find the length.
Volume
Example
Find the dimensions of a shipping box given that the length is twice the width, the height is [latex]8[/latex] inches, and the volume is [latex]1,600[/latex] in.3.Answer: The formula for the volume of a box is given as [latex]V=LWH[/latex], the product of length, width, and height. We are given that [latex]L=2W[/latex], and [latex]H=8[/latex]. The volume is [latex]1,600[/latex] cubic inches.
Think About It
Express the formula for the surface area of a cylinder, [latex]s=2\pi rh+2\pi r^{2}[/latex], in terms of the height, h. In this example, the variable h is buried pretty deeply in the formula for surface area of a cylinder. Using the order of operations, it can be isolated. Before you look at the solution, use the box below to write down what you think is the best first step to take to isolate h. [practice-area rows="1"][/practice-area]Answer: Isolate the term containing the variable, h, by subtracting [latex]2\pi r^{2}[/latex]from both sides.
[latex]\begin{array}{r}S\,\,=2\pi rh+2\pi r^{2} \\ \underline{-2\pi r^{2}\,\,\,\,\,\,\,\,\,\,\,\,\,-2\pi r^{2}}\\S-2\pi r^{2}\,\,\,\,=\,\,\,\,2\pi rh\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
Next, isolate the variable h by dividing both sides of the equation by [latex]2\pi r[/latex].[latex]\begin{array}{r}\Large\frac{S-2\pi r^{2}}{2\pi r}=\frac{2\pi rh}{2\pi r} \\\\\Large\frac{S-2\pi r^{2}}{2\pi r}=h\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
You can rewrite the equation so the isolated variable is on the left side.[latex]h=\Large\frac{S-2\pi r^{2}}{2\pi r}[/latex]
Isolate Variables in Formulas
Sometimes, it is easier to isolate the variable you you are solving for when you are using a formula. This is especially helpful if you have to perform the same calculation repeatedly, or you are having a computer perform the calculation repeatedly. In the next examples, we will use algebraic properties to isolate a variable in a formula.Example
Isolate the term containing the variable, w, from the formula for the perimeter of a rectangle:[latex]{P}=2\left({L}\right)+2\left({W}\right)[/latex].
Answer: First, isolate the term with w by subtracting 2l from both sides of the equation.
[latex] \displaystyle \begin{array}{l}\,\,\,\,\,\,\,\,\,\,p\,=\,\,\,\,2l+2w\\\underline{\,\,\,\,\,-2l\,\,\,\,\,-2l\,\,\,\,\,\,\,\,\,\,\,}\\p-2l=\,\,\,\,\,\,\,\,\,\,\,\,\,2w\end{array}[/latex]
Next, clear the coefficient of w by dividing both sides of the equation by [latex]2[/latex].[latex]\displaystyle \begin{array}{l}\underline{p-2l}=\underline{2w}\\\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\\ \,\,\,\Large\frac{p-2l}{2}\,\,=\,\,w\\\,\,\,\,\,\,\,\,\,\,\,w=\Large\frac{p-2l}{2}\end{array}[/latex]
You can rewrite the equation so the isolated variable is on the left side.[latex]w=\Large\frac{p-2l}{2}[/latex]
Example
Use the multiplication and division properties of equality to isolate the variable b given [latex]A=\Large\frac{1}{2}\normalsize bh[/latex]Answer:
[latex]\begin{array}{l}\,\,\,\,\,\,\,\,A=\Large\frac{1}{2}\normalsize bh\\\\\left(2\right)A=\left(2\right)\Large\frac{1}{2}\normalsize bh\\\\\,\,\,\,\,\,2A=bh\\\\\,\,\,\,\,\,\,\Large\frac{2A}{h}=\frac{bh}{h}\\\\\,\,\,\,\,\,\,\,\Large\frac{2A}{h}=\frac{b\cancel{h}}{\cancel{h}}\end{array}[/latex]
Write the equation with the desired variable on the left-hand side as a matter of convention:[latex]b=\Large\frac{2A}{h}[/latex]
Use the multiplication and division properties of equality to isolate the variable h given [latex]A=\Large\frac{1}{2}\normalsize bh[/latex]Answer:
[latex]\begin{array}{l}\,\,\,\,\,\,\,\,A=\Large\frac{1}{2}\normalsize bh\\\\\left(2\right)A=\left(2\right)\Large\frac{1}{2}\normalsize bh\\\\\,\,\,\,\,\,2A=bh\\\\\,\,\,\,\,\,\,\Large\frac{2A}{b}=\frac{bh}{b}\\\\\,\,\,\,\,\,\,\,\Large\frac{2A}{b}=\frac{h\cancel{b}}{\cancel{b}}\end{array}[/latex]
Write the equation with the desired variable on the left-hand side as a matter of convention:[latex]h=\Large\frac{2A}{b}[/latex]
Temperature
Let’s look at another formula that includes parentheses and fractions, the formula for converting from the Fahrenheit temperature scale to the Celsius scale.[latex]C=\left(F--32\right)\cdot\Large\frac{5}{9}[/latex]
Example
Given a temperature of [latex]12^{\circ}{C}[/latex], find the equivalent in [latex]{}^{\circ}{F}[/latex].Answer: Substitute the given temperature in[latex]{}^{\circ}{C}[/latex] into the conversion formula:
[latex]12=\left(F-32\right)\cdot\Large\frac{5}{9}[/latex]
Isolate the variable F to obtain the equivalent temperature.[latex]\begin{array}{r}12=\left(F-32\right)\cdot\Large\frac{5}{9}\\\\\left(\Large\frac{9}{5}\normalsize\right)12=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\\left(\Large\frac{108}{5}\normalsize\right)12=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\21.6=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\underline{+32\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+32}\,\,\,\,\,\,\,\,\,\,\,\,\\\\53.6={}^{\circ}{F}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]
Example
Solve the formula shown below for converting from the Fahrenheit scale to the Celsius scale for F. [latex-display]C=\left(F--32\right)\cdot\Large\frac{5}{9}[/latex-display]Answer: To isolate the variable F, it would be best to clear the fraction involving F first. Multiply both sides of the equation by [latex] \displaystyle \frac{9}{5}[/latex].
[latex]\begin{array}{l}\\\,\,\,\,\left(\Large\frac{9}{5}\normalsize\right)C=\left(F-32\right)\left(\Large\frac{5}{9}\normalsize\right)\left(\Large\frac{9}{5}\normalsize\right)\\\\\,\,\,\,\,\,\,\,\,\,\,\,\Large\frac{9}{5}\normalsize C=F-32\end{array}[/latex]
Add 32 to both sides.[latex]\begin{array}{l}\Large\frac{9}{5}\normalsize\,C+32=F-32+32\\\\\Large\frac{9}{5}\normalsize\,C+32=F\end{array}[/latex]
Answer
[latex]F=\Large\frac{9}{5}\normalsize C+32[/latex]Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra. Provided by: OpenStax Authored by: Abramson, Jay, et al.. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution. License terms: Download for free at : http://cnx.org/contents/[email protected]:1/Preface.
- Ex: Find the Dimensions and Area of a Field Given the Perimeter Mathispower4u . Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex: Find the Area of a Rectangle Given the Perimeter. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Find the Volume of a Right Circular Cylinder Formed from a Given Rectangle. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
