Read: Solutions for Systems of Linear Equations
Learning Objectives
- Recognize consistent and inconsistent, dependent and independent systems of linear equations
- Determine whether an ordered pair is a solution to a system of linear equations
- Solve a system of linear equations by graphing
[latex]\begin{array}{c}2x+y=\text{ }15\\ 3x-y=\text{ }5\end{array}[/latex]
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair [latex](4, 7)[/latex] is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly we will investigate methods of finding such a solution if it exists.
[latex]\begin{array}{l}2\left(4\right)+\left(7\right)=15\text{ }\text{True}\hfill \\ 3\left(4\right)-\left(7\right)=5\text{ }\text{True}\hfill \end{array}[/latex]
In addition to considering the number of equations and variables, we can categorize systems of linear equations by the number of solutions. A consistent system of equations has at least one solution. A consistent system is considered to be an independent system if it has a single solution, such as the example we just explored. The two lines have different slopes and intersect at one point in the plane. A consistent system is considered to be a dependent system if the equations have the same slope and the same y-intercepts. In other words, the lines coincide so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions.
Another type of system of linear equations is an inconsistent system, which is one in which the equations represent two parallel lines. The lines have the same slope and different y-intercepts. There are no points common to both lines; hence, there is no solution to the system.
A General Note: Types of Linear Systems
There are three types of systems of linear equations in two variables, and three types of solutions.- An independent system has exactly one solution pair [latex]\left(x,y\right)[/latex]. The point where the two lines intersect is the only solution.
- An inconsistent system has no solution. Notice that the two lines are parallel and will never intersect.
- A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.
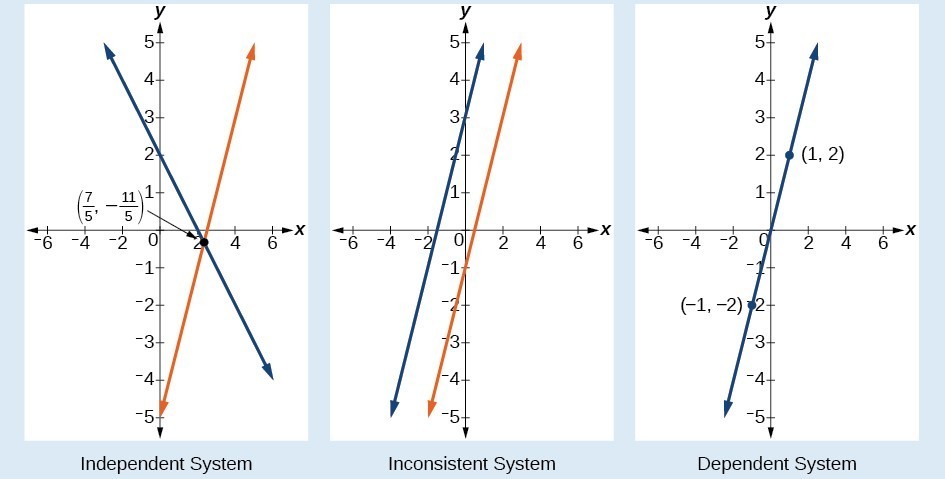The independent and dependent systems are also consistent because they both have at least one solution.
How To: Given a system of linear equations and an ordered pair, determine whether the ordered pair is a solution.
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.
Example
Determine whether the ordered pair [latex]\left(5,1\right)[/latex] is a solution to the given system of equations.[latex]\begin{array}{l}x+3y=8\hfill \\ 2x - 9=y\hfill \end{array}[/latex]
Answer: Substitute the ordered pair [latex]\left(5,1\right)[/latex] into both equations.
[latex]\begin{array}{ll}\left(5\right)+3\left(1\right)=8\hfill & \hfill \\ \text{ }8=8\hfill & \text{True}\hfill \\ 2\left(5\right)-9=\left(1\right)\hfill & \hfill \\ \text{ }\text{1=1}\hfill & \text{True}\hfill \end{array}[/latex]
The ordered pair [latex]\left(5,1\right)[/latex] satisfies both equations, so it is the solution to the system. We can see the solution clearly by plotting the graph of each equation. Since the solution is an ordered pair that satisfies both equations, it is a point on both of the lines and thus the point of intersection of the two lines.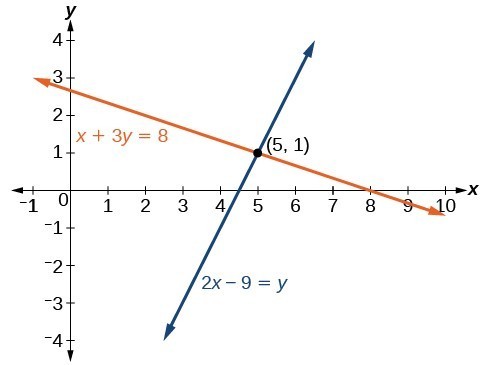
Solving Systems of Equations by Graphing
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.Example
Solve the following system of equations by graphing. Identify the type of system.[latex]\begin{array}{c}2x+y=-8\\ x-y=-1\end{array}[/latex]
Answer: Solve the first equation for [latex]y[/latex].
[latex]\begin{array}{c}2x+y=-8\\ y=-2x - 8\end{array}[/latex]
Solve the second equation for [latex]y[/latex].[latex]\begin{array}{c}x-y=-1\\ y=x+1\end{array}[/latex]
Graph both equations on the same set of axes as in the figure below.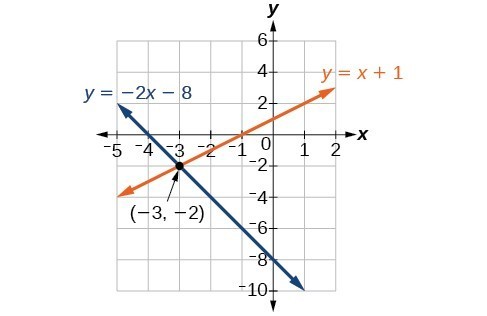
The lines appear to intersect at the point [latex]\left(-3,-2\right)[/latex]. We can check to make sure that this is the solution to the system by substituting the ordered pair into both equations
[latex]\begin{array}{ll}2\left(-3\right)+\left(-2\right)=-8\hfill & \hfill \\ \text{ }-8=-8\hfill & \text{True}\hfill \\ \text{ }\left(-3\right)-\left(-2\right)=-1\hfill & \hfill \\ \text{ }-1=-1\hfill & \text{True}\hfill \end{array}[/latex]
The solution to the system is the ordered pair [latex]\left(-3,-2\right)[/latex], so the system is independent.Licenses & Attributions
CC licensed content, Original
- Determine if an Ordered Pair is a Solution to a System of Linear Equations. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
- Determine the Number of Solutions to a System of Linear Equations From a Graph. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution.
CC licensed content, Shared previously
- Ex 2: Solve a System of Equations by Graphing. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
