Read: Systems of Three Equations in Three Variables
Learning Objectives
- Define the solution to a system of three equations in three variables
- Determine whether an ordered triple is a solution to a system
- Solve a systems of equations in three variables using elimination and back-substitution
Solution Set, One Solution
The figure below illustrates how a system with three variables can have one solution. Systems that have a single solution are those which result in a solution set consisting of an ordered triple [latex]\left(x,y,z\right)[/latex]. Graphically, the ordered triple defines a point that is the intersection of three planes in space.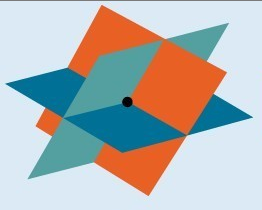
Example
Determine whether the ordered triple [latex]\left(3,-2,1\right)[/latex] is a solution to the system.Answer: We will check each equation by substituting in the values of the ordered triple for [latex]x,y[/latex], and [latex]z[/latex]. [latex-display]\begin{array}{ccccc}\begin{array}{r}\hfill x+y+z=2\\ \hfill \left(3\right)+\left(-2\right)+\left(1\right)=2\\ \hfill \text{True}\end{array}& & \begin{array}{r}\hfill \text{}6x - 4y+5z=31\\ \hfill 6\left(3\right)-4\left(-2\right)+5\left(1\right)=31\\ \hfill 18+8+5=31\\ \hfill \text{True}\end{array}& & \begin{array}{r}\hfill \text{}5x+2y+2z=13\\ \hfill 5\left(3\right)+2\left(-2\right)+2\left(1\right)=13\\ \hfill \text{}15 - 4+2=13\\ \hfill \text{True}\end{array}\end{array}[/latex-display] The ordered triple [latex]\left(3,-2,1\right)[/latex] is indeed a solution to the system.
How To: Given a linear system of three equations, solve for three unknowns.
- Pick any pair of equations and solve for one variable.
- Pick another pair of equations and solve for the same variable.
- You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
- Back-substitute known variables into any one of the original equations and solve for the missing variable.
Example
Solve the system [latex-display]\displaystyle\begin{cases}x-\dfrac{1}{3}y+\dfrac{1}{2}z=1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,y-\dfrac{1}{2}z=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,z=-1\end{cases}[/latex-display]Answer: The third equation states that [latex]z = −1[/latex], so we substitute this into the second equation to obtain a solution for [latex]y[/latex]. [latex-display]\begin{array}y-\dfrac{1}{2}(-1)=4\\y+\dfrac{1}{2}=4\\y=4-\dfrac{1}{2}\\y=\dfrac{8}{2}-\dfrac{1}{2}\\y=\dfrac{7}{2}\end{array}[/latex-display] Now we have two of our solutions and we can substitute them both into the first equation to solve for [latex]x[/latex]. [latex-display]\begin{array}x-\dfrac{1}{3}\left(\dfrac{7}{2}\right)+\dfrac{1}{2}\left(-1\right)=1\\x-\dfrac{7}{6}-\dfrac{1}{2}=1\\x-\dfrac{7}{6}-\dfrac{3}{6}=1\\x-\dfrac{10}{6}=1\\x=1+\dfrac{10}{6}\\x=\dfrac{6}{6}+\dfrac{10}{6}\\x=\dfrac{16}{6}=\dfrac{8}{3}\end{array}[/latex-display] Now we have our ordered triple, remember that where you place the solutions matters!
Answer
[latex-display](x,y,z)=\left(\dfrac{8}{3},\dfrac{7}{2},-1\right)[/latex-display]Analysis of the solution:
Each of the lines in this system represents a plane (think about a sheet of paper). If you imagine three sheets of notebook paper each representing a portion of these planes, you will start to see the complexities involved in how three such planes can intersect. Below is a sketch of the three planes. It turns out that any two of these planes intersect in a line, so our intersection point is where all three of these lines meet.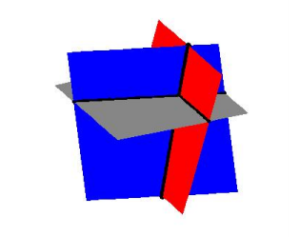 Three Planes Intersecting.
Three Planes Intersecting.Example
Find a solution to the following system:Answer:
[latex]\begin{array}{rrr}-2y+(6)=6\\-2y=6-6\\-2y=0\\\,\,\,\,y=0\end{array}[/latex]
Be careful here not to get confused with a solution of [latex]y = 0[/latex] and an inconsistent solution. It's ok for variables to equal [latex]0[/latex]. Now we can substitute [latex]z = 6[/latex] and [latex]y = 0[/latex] back into the original equation.[latex]\begin{array}{rrr}x-y+z=5\\x-0+6=5\\x+6=5\\x=5-6\\x=-1\end{array}[/latex]
Answer
[latex-display](x,y,z)=(-1,0,6)[/latex-display]Summary
- The solution to a system of linear equations in three variables is an ordered triple in the form [latex](x,y,z)[/latex]
- Solutions can be verified using substitution and the order of operations
- Systems of three variables can be solved using the same techniques as we used to solve systems with two variables, including elimination and substitution.
Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. License: CC BY: Attribution.
CC licensed content, Shared previously
- College Algebra: 8.1 Systems of Linear Equations: Gaussian Elimination. Authored by: Stitz, Carl and Zeager, Jeff. Located at: https://www.stitz-zeager.com/szca07042013.pdf. License: CC BY: Attribution.
- Ex: Solve a System of 3 Equations with 3 Unknowns Using Back Substitution. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 2: System of Three Equations with Three Unknowns Using Elimination. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 1: System of Three Equations with Three Unknowns Using Elimination. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
CC licensed content, Specific attribution
- Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution.
