Read: Identify a One-to-One Function
Learning Objectives
- Define one-to-one function
- Use the horizontal line test to determine whether a function is one-to-one
Example
Find the domain and range for the function.|
x |
y |
|---|---|
|
[latex]−5[/latex] |
[latex]−6[/latex] |
|
[latex]−2[/latex] |
[latex]−1[/latex] |
|
[latex]−1[/latex] |
[latex]0[/latex] |
|
[latex]0[/latex] |
[latex]3[/latex] |
|
[latex]5[/latex] |
[latex]15[/latex] |
Answer: The domain is the set of inputs or x-coordinates.
[latex]\{−5,−2,−1,0,5\}[/latex]
The range is the set of outputs of y-coordinates.[latex]\{−6,−1,0,3,15\}[/latex]
Answer
[latex-display]\begin{array}{l}\text{Domain}:\{−5,−2,−1,0,5\}\\\text{Range}:\{−6,−1,0,3,15\}\end{array}[/latex-display]
However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in.
| Letter grade | Grade point average |
|---|---|
| A | [latex]4.0[/latex] |
| B | [latex]3.0[/latex] |
| C | [latex]2.0[/latex] |
| D | [latex]1.0[/latex] |
This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.
To visualize this concept, let’s look again at the two simple functions sketched in (a)and (b) of Figure 10.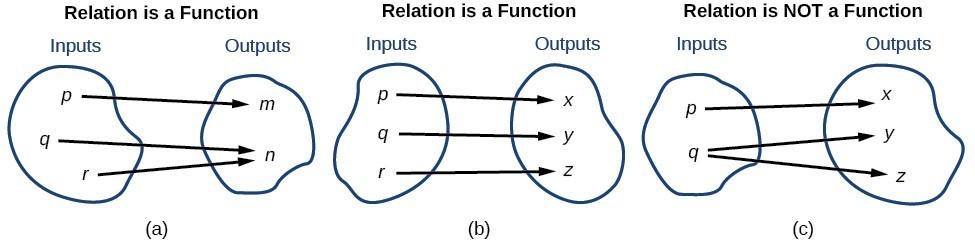 Figure 10
Figure 10A General Note: One-to-One Function
A one-to-one function is a function in which each output value corresponds to exactly one input value.Example
Which table represents a one-to-one function? a)| input | output |
| [latex]1[/latex] | [latex]5[/latex] |
| [latex]12[/latex] | [latex]2[/latex] |
| [latex]0[/latex] | [latex]-1[/latex] |
| [latex]4[/latex] | [latex]2[/latex] |
| [latex]-5[/latex] | [latex]0[/latex] |
| input | output |
| [latex]4[/latex] | [latex]8[/latex] |
| [latex]8[/latex] | [latex]16[/latex] |
| [latex]16[/latex] | [latex]32[/latex] |
| [latex]32[/latex] | [latex]64[/latex] |
| [latex]64[/latex] | [latex]128[/latex] |
Answer: Table a) maps the output value [latex]2[/latex] to two different input values, therefore this is NOT a one-to-one function. Table b) maps each output to one unique input, therefore this IS a one-to-one function.
Answer
Table b) is one-to-oneUsing the Horizontal Line Test
An easy way to determine whether a function is a one-to-one function is to use the horizontal line test on the graph of the function. To do this, draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.
How To: Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.
- Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
- If there is any such line, determine that the function is not one-to-one.
Exercises
For the following graphs, determine which represent one-to-one functions.
Answer:
The function in (a) is not one-to-one. Using the horizontal line test, as shown below, it intersects the graph of the function at two points (and we can even find horizontal lines that intersect it at three points.)

 The function (c) is not one-to-one, and is in fact not a function.
The function (c) is not one-to-one, and is in fact not a function.

Summary
In real life and in algebra, different variables are often linked. When a change in value of one variable causes a change in the value of another variable, their interaction is called a relation. A relation has an input value which corresponds to an output value. When each input value has one and only one output value, that relation is a function. Functions can be written as ordered pairs, tables, or graphs. The set of input values is called the domain, and the set of output values is called the range.Licenses & Attributions
CC licensed content, Original
- Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution.
CC licensed content, Shared previously
- Determine if a Relation Given as a Table is a One-to-One Function. Authored by: James Sousa (Mathispower4u.com) . License: CC BY: Attribution.
- Ex 1: Use the Vertical Line Test to Determine if a Graph Represents a Function. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution.
- Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education Located at: https://www.nroc.org/. License: CC BY: Attribution.
