Why It Matters: Quadratic Equations and Complex Numbers
Why learn about quadratic equations and complex numbers?
In algebra, a quadratic equation (from the Latin quadratus for "square") is any equation having the form[latex]ax^2+bx+c=0[/latex]
where x represents an unknown, and a, b, and c represent known numbers such that a is not equal to [latex]<span class="texhtml">0[/latex]. If a =[latex]0[/latex], then the equation is linear, not quadratic. The numbers a, b, and c are the coefficients of the equation, and may be distinguished by calling them, respectively, the quadratic coefficient, the linear coefficient and the constant or free term. Joan and her friend Hazel have decided to go cliff jumping at their favorite spot along the river. Hazel is an amateur photographer who just got a new camera that has a continuous shooting mode. Hazel takes a picture of Joan jumping off a cliff into the river that looks like this: Cliff jumping off a rock into the ocean - the trajectory of the cliff jumper is parabolic.
Cliff jumping off a rock into the ocean - the trajectory of the cliff jumper is parabolic.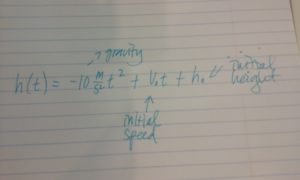
[latex]h(t)=-10\frac{m}{s^2}t^2+v_{o}t+h_{o}[/latex]
She had labeled the equation with arrows in the following way: [latex]-10\frac{m}{s^2}[/latex] is gravity, [latex]v_{o}[/latex] is the initial speed of the object, [latex]h_{o}[/latex] is the initial height of the object.
Hazel and Joan think they can figure out how long they were in the air as they jumped from the cliff into the river. Stay tuned for the end of the module when we see how they do it.
Learning Outcomes:
- Define and recognize a quadratic equation
- Solve quadratic equations using factoring, square roots, completing the square and the quadratic formula
- Recognize that the quadratic formula is a result of completing the square
- Define and recognize imaginary and complex numbers
- Perform algebraic operations on imaginary and complex numbers
- Solve quadratic equations that have complex solutions
- Use the discriminant to determine how many, and what type of solution(s) a quadratic equation will have
