We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts

Borda Count

Learning Outcomes

  • Determine the winner of an election using preference ballots
  • Evaluate the fairness of an election using preference ballots
  • Determine the winner of an election using the Instant Runoff method
  • Evaluate the fairness of an Instant Runoff election
  • Determine the winner of an election using a Borda count
  • Evaluate the fairness of an election determined using a Borda count
  • Determine the winner of en election using Copeland's method
  • Evaluate the fairness of an election determined by Copeland's method
Borda Count is another voting method, named for Jean-Charles de Borda, who developed the system in 1770.

Borda Count

In this method, points are assigned to candidates based on their ranking; 1 point for last choice, 2 points for second-to-last choice, and so on. The point values for all ballots are totaled, and the candidate with the largest point total is the winner.

Example

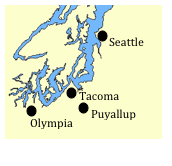
A group of mathematicians are getting together for a conference. The members are coming from four cities: Seattle, Tacoma, Puyallup, and Olympia. Their approximate locations on a map are shown below. A map of the Puget Sound. Seattle, Tacoma, Puyallup, and Olympia are marked. The votes for where to hold the conference were:
51 25 10 14
1st choice Seattle Tacoma Puyallup Olympia
2nd choice Tacoma Puyallup Tacoma Tacoma
3rd choice Olympia Olympia Olympia Puyallup
4th choice Puyallup Seattle Seattle Seattle
Use the Borda count method to determine the winning town for the conference.

Answer: In each of the 51 ballots ranking Seattle first, Puyallup will be given 1 point, Olympia 2 points, Tacoma 3 points, and Seattle 4 points. Multiplying the points per vote times the number of votes allows us to calculate points awarded

51 25 10 14
1st choice 4 points Seattle [latex]4\cdot51=204[/latex] Tacoma [latex]4\cdot25=100[/latex] Puyallup [latex]4\cot10=40[/latex] Olympia [latex]4\cdot14=56[/latex]
2nd choice 3 points Tacoma [latex]3\cdot51=153[/latex] Puyallup [latex]3\cdot25=75[/latex] Tacoma [latex]3\cdot10=30[/latex] Tacoma [latex]3\cdot14=42[/latex]
3rd choice 2 points Olympia [latex]2\cdot51=102[/latex] Olympia [latex]2\cdot25=50[/latex] Olympia [latex]2\cdot10=20[/latex] Puyallup [latex]2\cdot14=28[/latex]
4th choice 1 point Puyallup [latex]1\cdot51=51[/latex] Seattle [latex]1\cdot25=25[/latex] Seattle [latex]1\cdot10=10[/latex] Seattle [latex]1\cdot14=14[/latex]
Adding up the points: Seattle: [latex]204+25+10+14=253[/latex] points Tacoma: [latex]153+100+30+42=325[/latex] points Puyallup: [latex]51+75+40+28=194[/latex] points Olympia: [latex]102+50+20+56=228[/latex] points Under the Borda Count method, Tacoma is the winner of this vote.

Here is a video showing the example from above. https://youtu.be/vfujywLdW_s?list=PL1F887D3B8BF7C297

Try It

Consider again the election from earlier. Find the winner using Borda Count. Since we have some incomplete preference ballots, for simplicity, give every unranked candidate 1 point, the points they would normally get for last place.
44 14 20 70 22 80 39
1st choice G G G M M B B
2nd choice M B G B M
3rd choice B M B G G

What’s Wrong with Borda Count?

You might have already noticed one potential flaw of the Borda Count from the previous example. In that example, Seattle had a majority of first-choice votes, yet lost the election! This seems odd, and prompts our next fairness criterion:

Majority Criterion

If a choice has a majority of first-place votes, that choice should be the winner.
The election from the previous example using the Borda Count violates the Majority Criterion. Notice also that this automatically means that the Condorcet Criterion will also be violated, as Seattle would have been preferred by 51% of voters in any head-to-head comparison. Borda count is sometimes described as a consensus-based voting system, since it can sometimes choose a more broadly acceptable option over the one with majority support. In the example above, Tacoma is probably the best compromise location. This is a different approach than plurality and instant runoff voting that focus on first-choice votes; Borda Count considers every voter’s entire ranking to determine the outcome. Because of this consensus behavior, Borda Count, or some variation of it, is commonly used in awarding sports awards. Variations are used to determine the Most Valuable Player in baseball, to rank teams in NCAA sports, and to award the Heisman trophy.

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously