We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts

Exponential (Geometric) Growth

Learning Outcomes

  • Determine whether data or a scenario describe linear or geometric growth
  • Identify growth rates, initial values, or point values expressed verbally, graphically, or numerically, and translate them into a format usable in calculation
  • Calculate recursive and explicit equations for linear and geometric growth given sufficient information, and use those equations to make predictions

Population Growth

Suppose that every year, only 10% of the fish in a lake have surviving offspring. If there were 100 fish in the lake last year, there would now be 110 fish. If there were 1000 fish in the lake last year, there would now be 1100 fish. Absent any inhibiting factors, populations of people and animals tend to grow by a percent of the existing population each year. Two orange koi at the top of a pond, mouths open. Others are swimming beneath them. Suppose our lake began with 1000 fish, and 10% of the fish have surviving offspring each year. Since we start with 1000 fish, P­0 = 1000. How do we calculate P­1? The new population will be the old population, plus an additional 10%. Symbolically:

P­1 = P­0 + 0.10P­0

Notice this could be condensed to a shorter form by factoring:

P­1 = P­0 + 0.10P­0 = 1P­0 + 0.10P­0 = (1+ 0.10)P­0 = 1.10P­0

While 10% is the growth rate, 1.10 is the growth multiplier. Notice that 1.10 can be thought of as “the original 100% plus an additional 10%.” For our fish population,

P­1 = 1.10(1000) = 1100

We could then calculate the population in later years:

P­2 = 1.10P­1 = 1.10(1100) = 1210

P­3 = 1.10P2 = 1.10(1210) = 1331

Notice that in the first year, the population grew by 100 fish; in the second year, the population grew by 110 fish; and in the third year the population grew by 121 fish. While there is a constant percentage growth, the actual increase in number of fish is increasing each year. Graphing these values we see that this growth doesn’t quite appear linear.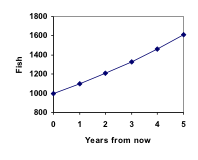 Line graph. Measured vertically: Fish, in increments of 200, from 800 to 1800. Measured horizontally: Years from now, measured in units of 1, from 0 to 5. Year 0 is at 1000; Year 1 is at roughly 1100; and subsequent years move in an increasing rate so that the overall line is curved to the upper right. A walkthrough of this fish scenario can be viewed here: https://youtu.be/3BiU7Ihxvxg To get a better picture of how this percentage-based growth affects things, we need an explicit form, so we can quickly calculate values further out in the future. Like we did for the linear model, we will start building from the recursive equation:

P­1 = 1.10P­0 = 1.10(1000)

P­2 = 1.10P­1 = 1.10(1.10(1000)) = 1.102(1000)

P­3 = 1.10P­2 = 1.10(1.102(1000)) = 1.103(1000)

P­4 = 1.10P­3 = 1.10(1.103(1000)) = 1.104(1000)

Observing a pattern, we can generalize the explicit form to be:

P­n = 1.10n(1000), or equivalently, P­n = 1000(1.10n)

From this, we can quickly calculate the number of fish in 10, 20, or 30 years: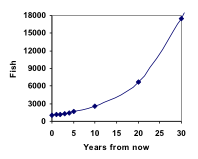 Line graph. Measured vertically: Fish, in increments of 3000, from 0 to 18,000. Measured horizontally: Years from now, measured in units of 5, from 0 to 30. Year 0 is at 1000, with a tight cluster of dots in the lower left quadrant. The exponential increase becomes more dramatic as time advances, so that year 30 is at 18,000 fish with more spacing between dots.

P­10 = 1.1010(1000) = 2594

P­20 = 1.1020(1000) = 6727

P­30 = 1.1030(1000) = 17449

Adding these values to our graph reveals a shape that is definitely not linear. If our fish population had been growing linearly, by 100 fish each year, the population would have only reached 4000 in 30 years, compared to almost 18,000 with this percent-based growth, called exponential growth. A video demonstrating the explicit model of this fish story can be viewed here: https://youtu.be/tg2ysaZ8agY In exponential growth, the population grows proportional to the size of the population, so as the population gets larger, the same percent growth will yield a larger numeric growth.  

Exponential Growth

If a quantity starts at size P­0 and grows by R% (written as a decimal, r) every time period, then the quantity after n time periods can be determined using either of these relations:

Recursive form

P­n = (1+r) P­n-1

Explicit form

P­n = (1+r)n P­0         or equivalently, P­n = P­0 (1+r)n

We call r the growth rate. The term (1+r) is called the growth multiplier, or common ratio.

Example

Between 2007 and 2008, Olympia, WA grew almost 3% to a population of 245 thousand people. If this growth rate was to continue, what would the population of Olympia be in 2014?

Answer: As we did before, we first need to define what year will correspond to n = 0. Since we know the population in 2008, it would make sense to have 2008 correspond to n = 0, so P­0 = 245,000.   The year 2014 would then be n = 6. We know the growth rate is 3%, giving r = 0.03. Using the explicit form:

P­6 = (1+0.03)6 (245,000) = 1.19405(245,000) = 292,542.25

The model predicts that in 2014, Olympia would have a population of about 293 thousand people.

The following video explains this example in detail. https://youtu.be/CDI4xS65rxY
 

Evaluating exponents on the calculator

To evaluate expressions like (1.03)6, it will be easier to use a calculator than multiply 1.03 by itself six times. Most scientific calculators have a button for exponents.  It is typically either labeled like:

^ ,   yx ,   or xy .

To evaluate 1.036 we’d type 1.03 ^ 6, or 1.03 yx 6.  Try it out - you should get an answer around 1.1940523.

Try It

India is the second most populous country in the world, with a population in 2008 of about 1.14 billion people. The population is growing by about 1.34% each year. If this trend continues, what will India’s population grow to by 2020?

Answer:

Using n = 0 corresponding with 2008, [latex]P_12= (1+0.0134)12(1.14)[/latex] = about 1.337 billion people in 2020

Example

Looking back at the last example, for the sake of comparison, what would the carbon emissions be in 2050 if emissions grow linearly at the same rate?

Answer: Again we will get n = 0 correspond with 1990, giving P­0 = 962. To find d, we could take the same approach as earlier, noting that the emissions increased by 220 million metric tons in 10 years, giving a common difference of 22 million metric tons each year. Alternatively, we could use an approach similar to that which we used to find the exponential equation. When n = 10, the explicit linear equation looks like:

P­10 = P­0 + 10d 

We know the value for P­0, so we can put that into the equation:

P­10 = 962 + 10d

Since we know that P­10 = 1182, substituting that in we get

1182 = 962 + 10d

We can now solve this equation for the common difference, d.

1182 – 962 = 10d

220 = 10d

d = 22

This tells us that if the emissions are changing linearly, they are growing by 22 million metric tons each year. Predicting the emissions in 2050,

P­60 = 962 + 22(60) = 2282 million metric tons.

You will notice that this number is substantially smaller than the prediction from the exponential growth model. Calculating and plotting more values helps illustrate the differences.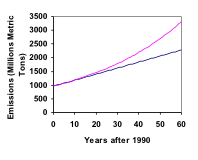 Line graph. Vertical measures Emissions (Millions Metric Tons) in increments of 500, from 0 to 3500. Horizontal measures Years after 1990, in increments of 10, from 0 to 60. A blue line shows a linear growth from 1000 in year 0 to over 2000 in year 60. A pink line shows an exponential growth from 1000 in year 0 to 3500 in year 60.

A demonstration of this example can be seen in the following video. https://youtu.be/yiuZoiRMtYM
So how do we know which growth model to use when working with data? There are two approaches which should be used together whenever possible:
  1. Find more than two pieces of data. Plot the values, and look for a trend. Does the data appear to be changing like a line, or do the values appear to be curving upwards?
  2. Consider the factors contributing to the data. Are they things you would expect to change linearly or exponentially? For example, in the case of carbon emissions, we could expect that, absent other factors, they would be tied closely to population values, which tend to change exponentially.

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Exponential (Geometric) Growth. Authored by: David Lippman. Located at: http://www.opentextbookstore.com/mathinsociety/. License: CC BY-SA: Attribution-ShareAlike.
  • calf-fish-lake-pond-river. Authored by: Pexels. License: CC0: No Rights Reserved.
  • Exponential Growth Model Part 1. Authored by: OCLPhase2's channel. License: CC BY: Attribution.
  • Exponential Growth Model Part 2. Authored by: OCLPhase2's channel. License: CC BY: Attribution.
  • Predicting future population using an exponential model. Authored by: OCLPhase2's channel. License: CC BY: Attribution.
  • Interpreting an Exponential Equation. Authored by: OCLPhase2's channel. License: CC BY: Attribution.
  • Finding an Exponential Model. Authored by: OCLPhase2's channel. License: CC BY: Attribution.
  • Comparing exponential to linear growth. Authored by: OCLPhase2's channel. License: CC BY: Attribution.
  • Question ID 6598. Authored by: Lippman, David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.