We've updated our
Privacy Policy effective December 15. Please read our updated Privacy Policy and tap

Study Guides > Mathematics for the Liberal Arts

Solve Exponentials for Time: Logarithms

Learning Outcomes

  • Evaluate and rewrite logarithms using the properties of logarithms
  • Use the properties of logarithms to solve exponential models for time
  • Identify the carrying capacity in a logistic growth model
  • Use a logistic growth model to predict growth

Reversing an Exponent

Earlier, we found that since Olympia, WA had a population of 245 thousand in 2008 and had been growing at 3% per year, the population could be modeled by the equation

P­n = (1+0.03)n (245,000), or equivalently, P­n = 245,000(1.03)n.

Using this equation, we were able to predict the population in the future. A soft-focus landscape photo of a crowd of people. Overlaid on top is a dotted red horizontal line and many vertical blue lines rising above and below the dotted red line, to give the impression of a population growth chart. Suppose we wanted to know when the population of Olympia would reach 400 thousand. Since we are looking for the year n when the population will be 400 thousand, we would need to solve the equation

400,000 = 245,000(1.03)n

Dividing both sides by 245,000 gives

1.6327 = 1.03n

  One approach to this problem would be to create a table of values, or to use technology to draw a graph to estimate the solution.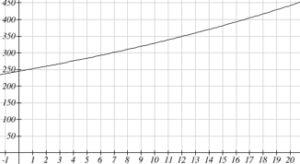 Line graph. Vertical measures increments of 50 from 0 to 450. Horizontal measures increments of 1 from 0 to 20. The line starts at 250/0, and moves in a sloping up trend towards 450/20. From the graph, we can estimate that the solution will be around 16 to 17 years after 2008 (2024 to 2025). This is pretty good, but we’d really like to have an algebraic tool to answer this question. To do that, we need to introduce a new function that will undo exponentials, similar to how a square root undoes a square. For exponentials, the function we need is called a logarithm. It is the inverse of the exponential, meaning it undoes the exponential. While there is a whole family of logarithms with different bases, we will focus on the common log, which is based on the exponential 10x.

Common Logarithm

The common logarithm, written log(x), undoes the exponential 10x This means that log(10x) = x, and likewise 10log(x) = x This also means the statement 10a = b is equivalent to the statement log(b) = a log(x) is read as “log of x”, and means “the logarithm of the value x”. It is important to note that this is not multiplication – the log doesn’t mean anything by itself, just like √ doesn’t mean anything by itself; it has to be applied to a number.

Example

Evaluate each of the following
  1. log(100)
  2. log(1000)
  3. log(10000)
  4. log(1/100)
  5. log(1)

Answer:

  1. log(100) can be written as log(102). Since the log undoes the exponential, log(102) = 2
  2. log(1000) = log(103) = 3
  3. log(10000) = log(104) = 4
  4. Recall that [latex]{{x}^{-n}}=\frac{1}{{{x}^{n}}}[/latex].   [latex]\log\left(\frac{1}{100}\right)=\log\left({{10}^{-2}}\right)=-2[/latex]
  5. Recall that x0 = 1.   log(1) = log(100) = 0

  This property will finally allow us to answer our original question.

Solving exponential equations with logarithms

  1. Isolate the exponential. In other words, get it by itself on one side of the equation. This usually involves dividing by a number multiplying it.
  2. Take the log of both sides of the equation.
  3. Use the exponent property of logs to rewrite the exponential with the variable exponent multiplying the logarithm.
  4. Divide as needed to solve for the variable.

Example

If Olympia is growing according to the equation, P­n = 245(1.03)n, where n is years after 2008, and the population is measured in thousands. Find when the population will be 400 thousand.

Answer: We need to solve the equation

400 = 245(1.03)n                     Begin by dividing both sides by 245 to isolate the exponential

1.633 = 1.03n                             Now take the log of both sides

log(1.633) = log(1.03n)            Use the exponent property of logs on the right side

log(1.633)= n log(1.03)            Now we can divide by log(1.03)

[latex]\frac{\log(1.633)}{\log(1.03)}=n[/latex]                       We can approximate this value on a calculator

n ≈ 16.591

A full walkthrough of this problem is available here. https://youtu.be/liNffAACIUs
Alternatively, after applying the exponent property of logs on the right side, we could have evaluated the logarithms to decimal approximations and completed our calculations using those approximations, as you’ll see in the next example. While the final answer may come out slightly differently, as long as we keep enough significant values during calculation, our answer will be close enough for most purposes.

Example

Polluted water is passed through a series of filters. Each filter removes 90% of the remaining impurities from the water. If you have 10 million particles of pollutant per gallon originally, how many filters would the water need to be passed through to reduce the pollutant to 500 particles per gallon?

Answer: In this problem, our “population” is the number of particles of pollutant per gallon. The initial pollutant is 10 million particles per gallon, so P0 = 10,000,000. Instead of changing with time, the pollutant changes with the number of filters, so n will represent the number of filters the water passes through. Also, since the amount of pollutant is decreasing with each filter instead of increasing, our “growth” rate will be negative, indicating that the population is decreasing instead of increasing, so r = -0.90. We can then write the explicit equation for the pollutant:

Pn = 10,000,000(1 – 0.90)n = 10,000,000(0.10)n

To solve the question of how many filters are needed to lower the pollutant to 500 particles per gallon, we can set Pn equal to 500, and solve for n.

500 = 10,000,000(0.10)n                     Divide both sides by 10,000,000

0.00005 = 0.10n                                     Take the log of both sides

log(0.00005) = log(0.10n)                    Use the exponent property of logs on the right side

log(0.00005) = n log(0.10)                   Evaluate the logarithms to a decimal approximation

-4.301 = n (-1)                                          Divide by -1, the value multiplying n

4.301 = n

It would take about 4.301 filters. Of course, since we probably can’t install 0.3 filters, we would need to use 5 filters to bring the pollutant below the desired level.

More details about solving this scenario are available in this video. https://youtu.be/sLLu0u1YgM0
 

Try It

India had a population in 2008 of about 1.14 billion people. The population is growing by about 1.34% each year. If this trend continues, when will India’s population reach 1.2 billion?  

TIP

When you are solving growth problems, use the language in the question to determine whether you are solving for time, future value, present value or growth rate. Questions that uses words like "when", "what year", or "how long" are asking you to solve for time and you will need to use logarithms to solve them because the time variable in growth problems is in the exponent.

Licenses & Attributions

CC licensed content, Original

CC licensed content, Shared previously

  • Solve Exponentials for Time: Logarithms. Authored by: David Lippman. Located at: http://www.opentextbookstore.com/mathinsociety/. License: CC BY-SA: Attribution-ShareAlike.
  • population-statistics-human. Authored by: geralt. License: CC BY: Attribution.
  • Using logs to solve for time. Authored by: OCLPhase2's channel. License: CC BY: Attribution.
  • Using logs to solve an exponential. Authored by: OCLPhase2's channel. License: CC BY: Attribution.
  • Question ID 100163. Authored by: Rieman,Rick. License: CC BY: Attribution.
  • Question ID 1764. Authored by: Lippman,David. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.
  • Question ID 34625. Authored by: Smart,Jim. License: CC BY: Attribution. License terms: IMathAS Community License CC-BY + GPL.